考虑乘客出行习惯的公交线网优化方法*

2018-10-12王佳冬袁振洲

交通信息与安全 2018年4期

王佳冬袁振洲

(北京交通大学城市交通复杂系统理论与技术教育部重点实验室北京 100044)

0 引言

公共交通线网的优化要兼顾乘客用户的利益和公交企业的利益，以系统效益最大化为目标，布设满足乘客出行需求的公交网络。公交乘客尤其是通勤、通学乘客在选择线路时通常表现出对既有线路的“黏性”[1]，笔者在论文中将此定义为“公交乘客出行习惯”，即乘客总是倾向于选择经常乘坐的线路，而且这种出行决策惯性是有限理性的体现。不合理的线网调整可能会打破乘客的出行习惯，无法在短时间内适应新的公交网络，调整线路不当会引起乘客满意度降低和公交吸引力下降。在实践中公交企业通常会充分考虑居民意见保留部分线路，在线路调整和站点设置上尽量符合居民的出行习惯。如何在线网优化理论模型的构建过程中科学地考虑乘客的出行习惯，减少线路或站点调整引起的公交客流损失，这是理论研究和运营实践中都亟待解决的重点和难点问题。

影响公交线网优化问题的因素和约束条件较多，国内外学者从各个角度进行了不同侧重的研究。W. Szeto等[2]使用最优策略[3]进行客流分配并建立以换乘次数最少为目标的双层规划模型，A. Renato等[4]分别以乘客总成本和企业成本最小为目标建立多目标优化模型，A. Mahdi等[5]考虑了公交需求的时变性，建立以不同季节乘客出行成本之和最小为目标的优化模型，Y. Baozhen等[6]基于公交行程时间可靠性，建立以乘客平均出行时间最小、换乘次数最少为目标的优化模型。俞礼军等[7]以发车频率为变量，建立以乘客出行成本与公交运营成本之和最小为目标的整数非线性规划模型，王殿海等[8]建立以人均舒适度最大为目标的优化模型，柏伟等[9]基于中间站最优建立以不产生排队的公交车辆数最大为目标的优化模型。

当前，对于出行习惯的研究主要集中于出行方式或出行路径选择行为方面。杨忠振等[10]基于累积前景理论分析了出行习惯对乘客机场选择行为的影响，提出了乘客选择习惯经过连续多次的选择过程会逐渐转换。宗芳等[11]基于SP调查建立了考虑出行习惯和路况的小汽车出行路径选择Logit模型，通过参数标定发现出行习惯对出行者路径选择的影响更大。鲁光泉[12]研究了考虑出行异质性的路径选择模型，研究发现出行者为了规避风险更倾向于保守地选择出行时间较长的习惯路径。Z. Junlin等[13]首次给出路径选择惯性的定义，认为不同OD对的出行者具有各自的惯性模式，即路径选择子集，并建立了惯性用户均衡模型。宋晓豆等[14]提出了出行者决策惯性是有限理性的一种体现，在有限理性用户均衡模型的基础上建立了基于可接受路径准则的多用户均衡模型。

目前在公交线网优化中考虑乘客出行习惯的研究较少，现有的研究大多对既有线路采取调整、保留、拆分等策略，对单条线路逐一优化调整，较少从全局角度定量分析乘客出行习惯。本文在以往研究的基础上，引入乘客出行习惯成本来反映线路调整对出行习惯的影响，以首末站布局要求、发车频率和换乘次数等为约束，兼顾乘客出行成本和公交运营成本，以系统总成本最低为目标建立优化模型，并以莱州市公交线网优化为例进行了实例分析和应用，给出了线路最优组合的推荐方案。

1 数学模型

1.1 模型假设

针对公交线网优化实际问题的特性，在将实际问题抽象、建模过程中，模型前提条件如下。

1) 公交线路上、下行发车频率相同，发车频率固定不变。

2) 公交车辆在路网中各路段行驶速度相同，公交车辆车型统一。

3) 乘客最多能接受1次换乘，2次及2次以上换乘视为不可达。

4) 乘客总是选择最短路径出行。

5) 以交通小区为分析单元，公交站点位于交通小区的质心，不考虑乘客步行时间。

1.2 网络描述

给定道路网络G(N,A)。N为节点集合，i∈N为路网节点;A为路段集合，a∈A为路段，la为路段a的长度，路网中共有W个OD对。公交备选线路集合为R*，被选中线路集合为R，公交线路r，假定路网的公交出行需求已知且不变，假定发车频率固定不变，第w(w∈W)个OD对(i,j)之间的最短公交路径lij由R确定，L(R)为公交路径集合。

1.3 乘客出行习惯成本

1) 乘客出行习惯成本的形成。所谓乘客出行习惯是乘客对公交服务的既有体验。当线网优化调整时，服务水平发生变化，当实际服务水平低于乘客既有体验时，乘客极有可能放弃公交，选择其他交通方式出行，造成公交客流损失，公交出行分担率下降，即产生乘客出行习惯成本。乘客出行习惯成本的形成过程见图1。

图1 乘客出行习惯成本形成过程Fig.1 Formation of passenger trip habit cost

乘客出行习惯成本是当公交服务水平不能达到乘客既有体验时所产生的一种隐性损失。由于乘客出行习惯成本的潜在性，既有的公交线网优化研究中往往忽略了这一点，导致优化后线网方案的服务水平无法满足部分乘客的预期，低水平的公交服务将直接或间接降低乘客对公交服务的整体满意度，从而造成客流损失。换言之，乘客出行习惯成本就是实际服务水平与乘客既有体验之间的差距。这种差距主要体现在2个方面：换乘次数和出行时间。

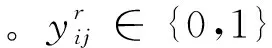
(1)

式中：qij为i与j间的OD需求;cr为车内时间价值，优化前的线路集合为R′，备选公交线路集合为R*。

(2)

综上所述，乘客出行习惯成本可表示为

(3)

式中：μ为习惯成本增大系数，表示乘客对出行习惯成本的敏感程度，μ越大，乘客对于增加的车内时间和换乘次数越敏感。

1.4 公交线网优化模型

以乘客出行成本和公交运营成本之和最小为优化目标，以首末站布局要求、发车频率和换乘次数等为约束建立整数规划模型。其中乘客出行成本包括等车时间成本、车内时间成本、换乘成本、乘车费用和乘客出行习惯成本。车内时间成本和换乘成本的计算方法与乘客出行习惯成本相同，不再赘述。

1) 等车时间成本。包括直达乘客和换乘乘客的等车时间。换乘乘客需要2次等车，因换乘产生第2次等车的时间价值应高于第1次，因此换乘乘客的平均等车时间价值也应高于直达乘客。则直达乘客和换乘乘客的等车时间成本分别为

(4)

(5)

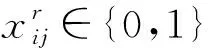
2) 乘车费用。公交票价统一为F，乘车费用表示为

3) 公交运营成本。公交运营成本考虑人工、燃油等成本，与总运营公里数成正比，公交运营成本Co为

式中：co为每公里公交运营成本；fr为公交线路r的发车频率；lr为公交线路r的长度。

综上所述，可得优化模型为

minZ=Cw+Cr+Ct+Cf+Ch+Co=

(6)

s.t. 5 km≤lr≤15 km

(7)

(8)

3 veh/h≤fr≤20 veh/h

(9)

(10)

(11)

(12)

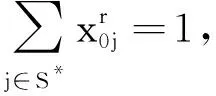
(13)

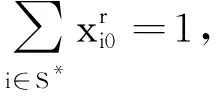
(14)

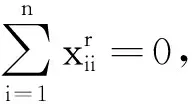
(15)

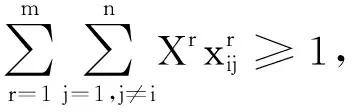
(16)

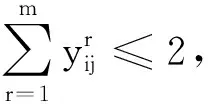
(17)

(18)

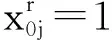
2 模型求解

模型求解思路为：首先生成公交候选线路集合，从中随机选出若干线路作为线网方案，其次将乘客OD需求分配到各条线路上，最后通过算法得出最优线路组合。分配的方法是最短路法，若最短路径不止1条，则分配到平均等车时间最小的线路上。需要说明的是，假设公交站点位于交通小区质心，公交线路为规划区域内经过各个交通小区的线路走向，而非实际站点连接形成的线路。所生成的线路还需结合实际道路网进行站点布设。

2.1 生成备选线路集合

包括新增备选线路集合与既有备选线路集合。新增备选线路采用K短路算法生成，通过筛选删除不满足线路长度约束和非直线系数约束的线路，确定新增备选线路集R1⊆R*。使用文献[17]的方法对既有线路采用延长、缩短、微调3种调整策略，通过筛选后生成既有备选线路集合R2⊆R*。

2.2 算法步骤

公交线网优化是公认的NP-Hard问题，随着实际问题规模扩大，模型的复杂程度和求解难度急剧增加，使用传统优化算法难以得到满意的最优解。在交通运输优化领域中遗传算法具有良好的优化效果[17]，因此采用遗传算法作为核心算法。为克服标准遗传算容易陷入局部最优解和早熟的缺点，采用多种群遗传算法，引入多个种群同时进行优化搜索，算法流程见图2。

算法执行步骤如下。

步骤1。初始化，确定遗传算法的参数，包括种群数目MP，种群规模N，染色体最大长度lenc，交叉概率pc，变异概率pm，最优个体最少保持代数gen0。确定模型参数，包括线路配车数、等车时间价值、车内时间价值等。

步骤2。随机生成初始种群，即随机确定每一条染色体的基因组成，每1个染色体代表1个线网方案。染色体中的每1个基因表示1条可行线路，采用二进制编码，基因值为1代表备选线路被选中，基因值为0代表备选线路未被选中。

步骤3。根据染色体编码得到对应的线网方案，计算目标函数和个体适应度值。适应度函数为

式中：P1为不满足公交运力约束的惩罚项;P2为超过车队规模限制的惩罚项;P3为不满足公交线路数量限制的惩罚项;P4为不满足公交站点全覆盖约束惩罚项;P1=P2=P3=P4=Cmax，元，Cmax取极大正整数;P5为不满足换乘次数约束的惩罚项，P5可表示为

式中：p为惩罚因子，元，取值为1 000。

步骤4。各初始种群按照标准遗传算法的步骤，进行选择、交叉、变异和重组等操作产生新一代的群体。为了兼顾算法的全局和局部搜索能力，每个种群的pc和pm在取值范围内随机生成，pc取值范围为(0.6～0.9)，pm取值范围为(0.01～0.05)。采用均匀交叉算子和单点变异算子，重组操作采用个体最优保留策略，即用父代最优个体替换子代最差个体，将其加入到子代种群中。

步骤5。移民算子用种群i的最优个体替换掉种群i+1的最差个体。

步骤6。人工选择算子选出每个种群的最优个体作为精华个体。

步骤7。判断是否达到终止条件。判断当前最有个体保留代数是否大于设定的最优个体最少保留代数gen0，若满足终止条件则停止迭代并输出最优解，否则返回步骤4。

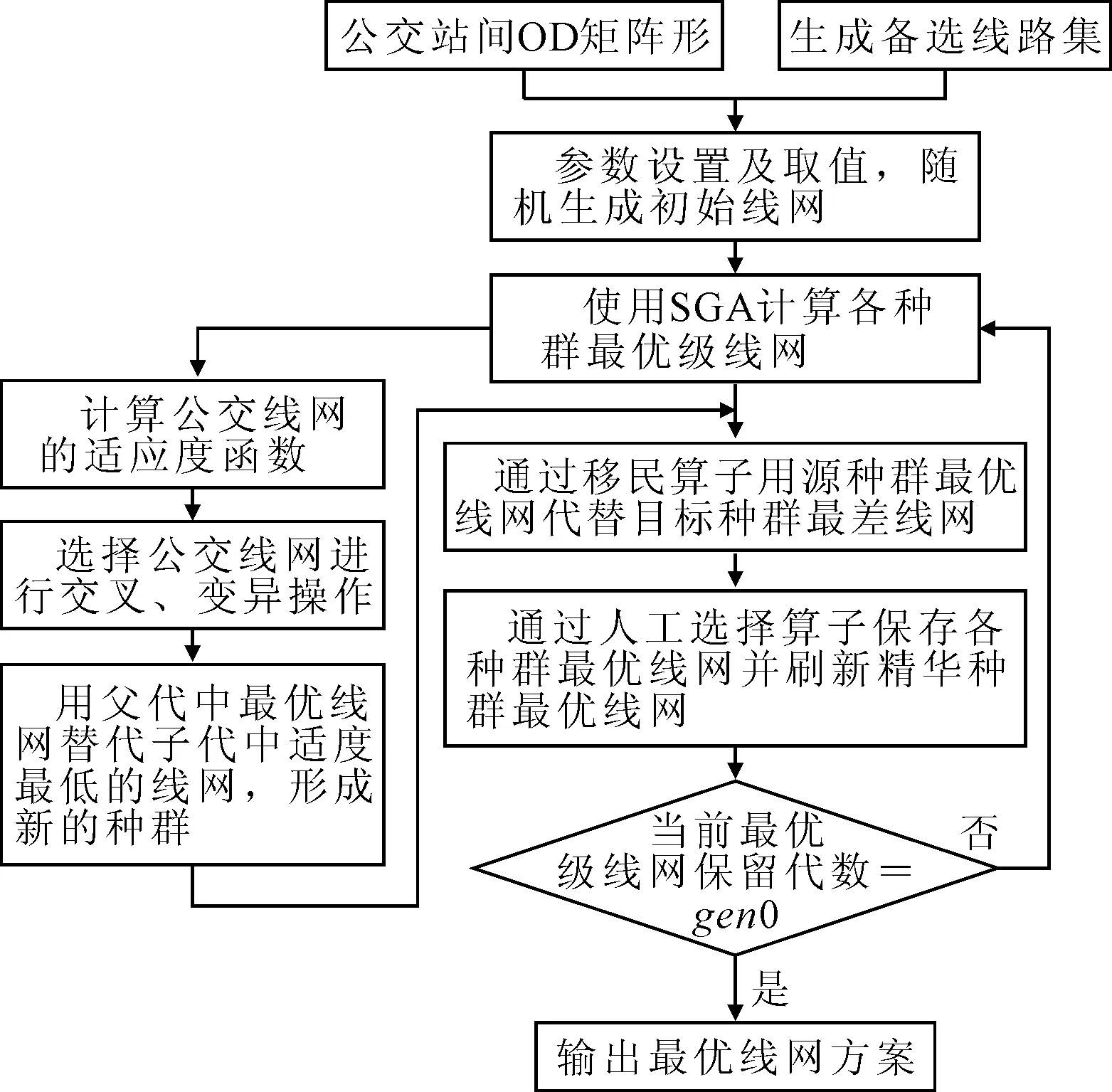
图2 算法流程图Fig.2 Algorithm Flow Chat

3 案例分析

3.1 案例说明

以山东省莱州市为例，划分27个交通小区，见图3。该网络由27个站点，96条路段组成，每个路段都是双向的，见图4。研究时段为早高峰：07：30—08:30，各小区间OD量已知，各路段长度已知。根据文献[18]，选用人均可支配收入计算乘客出行时间价值。根据国家统计局公布的2017年山东省居民收入情况，山东省2017年城镇居民人均可支配收入为36 789元，人均工作时间为每周44 h，则莱州市的乘客出行时间价值为16 元/(人·h)，因此乘客车内时间价值为16 元/(人·h)。文献[19]研究发现等车时间价值约为车内时间价值的2～3倍，因此，直达乘客等车时间价值取值为32 元/(人·h)，换乘乘客等车时间价值取值为48 元/(人·h)。综合考虑换乘不方便程度、乘客出行心里等因素，公交换乘惩罚因子Tp取10 min[14]。客车运营成本主要包括燃油消耗、人员工资等，加上车胎损耗费、人员费用、企业运转办公费用等，折合的公交运营成本为30 元/(车·km)[7]。出行惯性阈值θh=0.4[20]，平均停站时间τ为1 min，车辆载客容量为60人，根据调查，莱州市公交行驶车速为30 km/h。车队规模上限为200辆，由既有线路生成的备选线路配车数不变，见表1，新增线路的配车数均为12辆，线路发车频率根据配车数和周转时间计算；规划线路数量为10～20条，公交场站所在交通小区为{7,16,18,21,22,25,27} ，线路非直线系数NLr≤1.4。经筛选共生成既有备选线路45条，新增备选线路346条。种群遗传算法染色体种群数量为10，种群规模为20，最优个体最少保持代数为100，交叉概率pc取值范围为0.6～0.9，变异概率pm取值范围0.01～0.05。

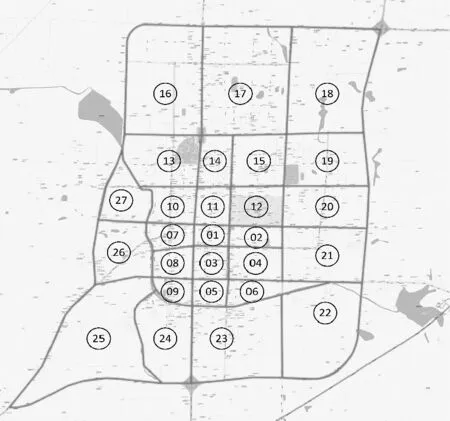
图3 实例小区划分Fig.3 Traffic zone division

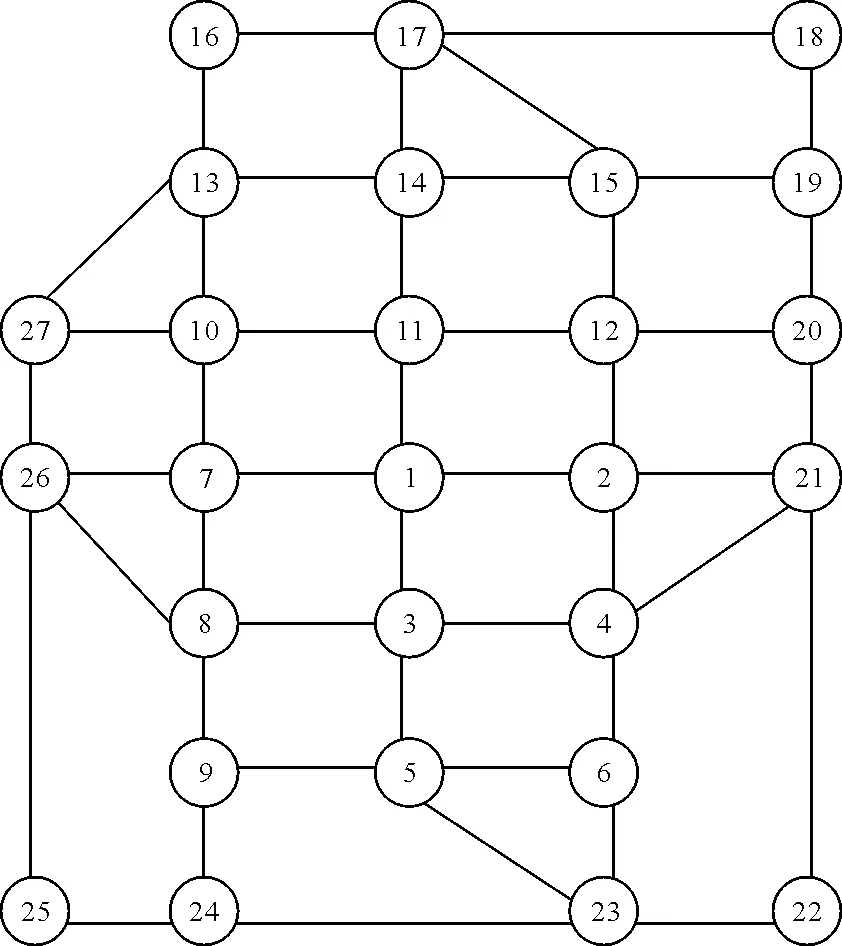
图4 实例网络示意图Fig.4 An Example of Network

3.2 优化结果及分析

根据以上参数，利用Matlab编程设计算法对模型进行求解，求解结果如表2所示。经过有限次计算取总成本最小的1次为优化方案，优化方案总成本为148 754 元，其中公交运营成本为47 265元，乘客出行成本为101 589元，图5为适应度函数变化趋势，运行到184代收敛。优化方案包括16条线路。

表1 优化前既有线路

表2 实例优化结果

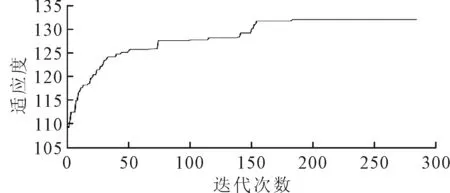
图5 进化过程Fig.5 Evolutionary process

将优化方案与现状方案进行对比，对比结果见表 3。优化方案总成本减少了1.8%，公交运营成本增加50.1%，线网规模增加52.4%，公交运营成本与线网规模呈正相关关系。优化前平均每公里线路的运营成本为240 元，优化后为236.3 元，虽然公交运营的总成本上升，但是线路的平均运营成本略有下降。乘客出行成本减少15.4%，其中等车时间成本减少19.6%，车内时间成本减少6.4%，换乘成本减少61.5%，乘车费用减少13.2%，线网优化后产生的出行习惯成本为1 330 元。

表3 实例优化前后对比

在公交网络设计中，常用乘客换乘次数比例来衡量公交网络的表现，表4给出了优化后线网方案与优化前直达乘客比例和1次换乘比例和不可达比例，优化后直达乘客比例提高了19.6%，可达比例为100%。表明提出的优化模型能减少乘客换乘次数，提高直达率。

表4 乘客换乘次数比例

将不考虑出行习惯的传统模型与改进模型进行对比，传统模型的最优方案见表5，二者最优方案对比结果见表6。对比分析可知：2种方案的总成本非常接近，改进模型最优方案与传统模型相比，公交运营成本增加6.0%，乘客出行成本减少2.6%。其中等车时间成本减少2%，车内时间成本减少0.8%，换乘成本减少6.5%，乘车费用减少1.9%，出行习惯成本减小43.4%，说明改进模型在不显著增加系统总成本的前提下能够减少线路调整对出行习惯的影响，更符合乘客的出行习惯。

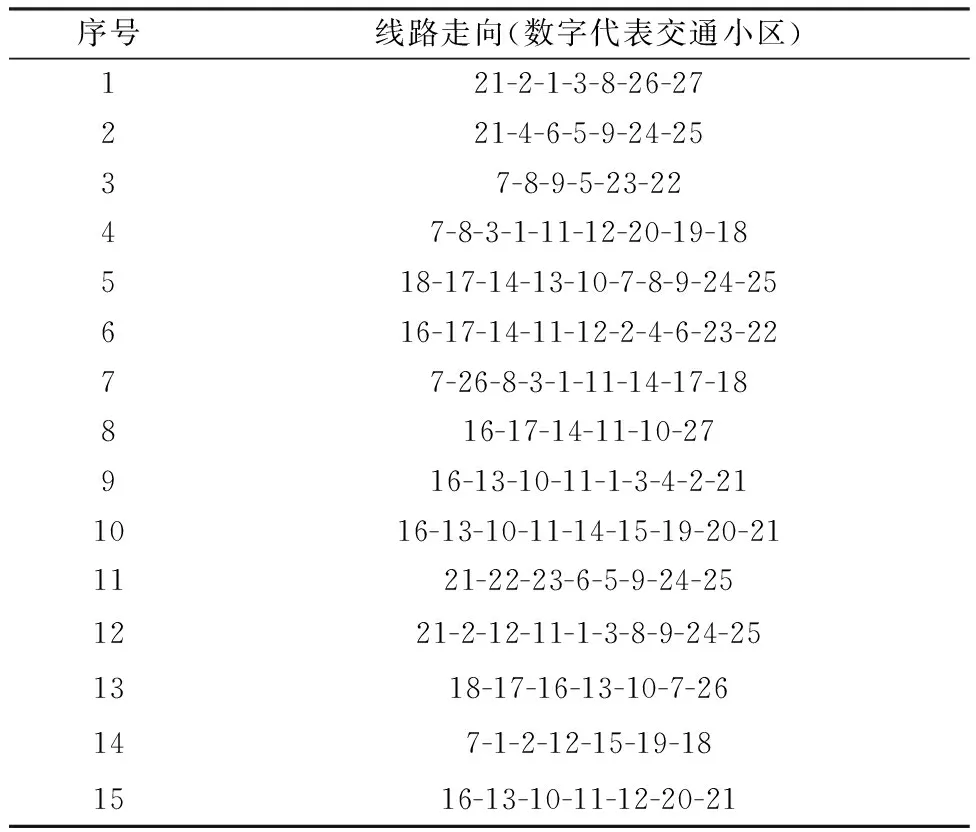
表5 传统模型的最优方案

表6 最优方案对比

3.3 灵敏度分析

分别选取不同的出行惯性阈值θh和习惯成本增大系数μ进行灵敏度分析。θh分别取0.1，0.2和0.4，μ分别取1.0，1.5和2。乘客出行习惯成本的变化见图6。

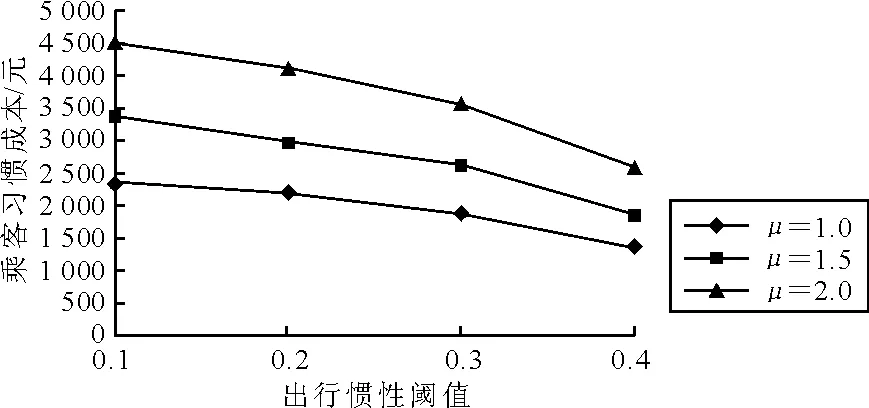
图6 θh和μ变化灵敏度分析Fig.6 Sensitivity analysis of θhandμ

由图6可见，当出行惯性阈值θh不变时，乘客出行习惯成本随μ的增大而增大；当习惯成本增大系数μ不变时，乘客出行习惯成本随θh的增大而减小。这是由于案例为中小城市，平均乘距较小，当θh增大时，车内时间超出阈值的乘客数量迅速减少。另外，当θh、μ变化时总成本变化幅度不大，这是由于在总成本最优的情况下，出行习惯受影响的乘客数量较少，乘客出行习惯成本在总成本中的比重较低，例如当θh=0.2，μ=1.5时，比重仅为2.04% 。