慢脉动B型星KIC 8324482的星震学研究∗

2018-10-12邓真敏1焱1涛1陈兴浩1

天文学报 2018年5期

关键词：颗星对流恒星

邓真敏1,2,3† 李焱1,2,3,4‡ 吴涛1,2 陈兴浩1,2

(1中国科学院云南天文台昆明650011)

(2中国科学院天体结构与演化重点实验室昆明650011)

(3中国科学院大学北京100049)

(4中国科学院天文大科学研究中心北京100012)

1 引言

在赫罗图的主序带的高光度段存在一类脉动周期较长(0.5–3 d)而光变幅度较低(大概小于0.04 mag)的多周期变星.在1991年,Waelkens[1]首次将这类变星命名为慢脉动B型(Slowly Pulsating B-type,SPB)星.SPB星属于非径向g模式振动[2],其激发机制是由不透明度引起的κ机制[3−4].现有观测、研究表明,SPB星的质量范围大概在2.5–8 M⊙之间,光谱型在B3–B9范围内,有效温度为11000–22000 K[1−5].

由于SPB星的脉动周期较长且振幅较小,因此地面观测设备很难获取其精确的脉动信息.直到近些年来MOST(Microvariablity and Oscillations of Stars)[6]、CoRoT(Convection Rotation and planetary Transits)[7]和Kepler[8]等高精度空间卫星的投放使用,使得星震学的研究领域取得突破性的进展,也让越来越多SPB星高精度的连续光谱数据被观测到.

SPB星是属于中等质量的上主序(Upper-Main-Sequence,UMS)星,这类恒星的内部结构是由一个辐射平衡壳层和一个正在逐渐收缩的中心对流核组成,在其对流核边界附近有着极为复杂的物理过程.目前,我们对于SPB星的研究还处于早期阶段,对这些物理过程还没有足够深入的了解.

星震学方法是一个可以探测恒星内部结构和状态的非常有效的工具,过去由于没有足够高精度的光谱数据,我们很难用这种方法来对SPB星进行诊断.但是现在如Kepler这样高精度长周期的观测任务却给我们提供了这个机会,目前对SPB星的星震学研究也取得了一定的进展.鲁汶大学的P´apics等[9]和Moravveji等[10]用星震学方法对一颗旋转非常慢的SPB星KIC 10526294进行了细致的诊断,判定这颗SPB星是一颗处于主序早期的恒星,并确定了这颗星的一些基本参数.此外,他们还得出结论:在这颗星的辐射壳层应该加入一个不大但是必要的全局扩散.同时他们还证明了采用指数衰减的函数来处理超射区扩散系数比用阶跃式的函数能更好地描述观测数据.

之后,P´apics等[11]和Moravveji等[12]又以一颗与KIC 10526294比较相似的SPB星KIC 7760680作为研究对象,对其进行星震学诊断分析,两颗恒星的不同之处在于后者的旋转速度比前者快得多.他们确定了这颗星的质量大概为3.25 M⊙,旋转频率为0.4805 d−1.同时他们还推断出这颗星的中心对流核边界应加入一个参数为fov=0.024±0.001的指数衰减对流超射,这证明了超射和旋转是可以共存的.

在本次研究工作中,我们选取KIC 8324482这颗SPB星作为研究对象,用星震学的方法来对这颗星进行诊断.一方面,我们可以确定这颗星的一些基本参数,了解其内部混合过程.另一方面,不同于KIC 10526294和KIC 7760680这两颗处于主序早期(零龄主序附近)的恒星,在我们前一个工作中,通过周期间隔的变化行为我们发现KIC 8324482处于主序演化的中期.随着中心核的收缩,这个时期的恒星中心氢燃料逐渐减少,在对流核和辐射平衡壳层之间形成一个相对主序早期较大的化学丰度梯度面.所以对这颗星的研究给我们提供了一个很好的机会,去探索这个化学梯度与恒星振动性质之间的关系.

2 g模的性质

SPB星的振动模式是非径向的g模式振动,由于g模是由恒星内部的浮力所引发的振动模式,因此其震荡性质完全由浮力频率N(也被叫作频率)来决定[2]:

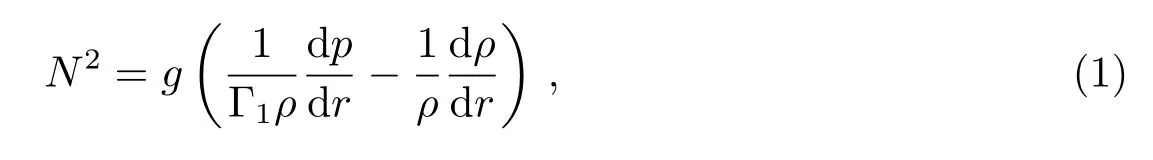
其中,g表示当地重力,r表示径向坐标,ρ为密度,p为压强,而Γ1则代表一阶绝热指数.对于完全电离的理想气体,N2可以近似表示为[2,13]:

上式中的∇ad、∇和∇µ分别为绝热温度梯度、温度梯度以及分子量梯度.

对于g模式震荡,在不考虑自转的情况下,球谐度l相同的模式的周期序列应该是等周期间隔的.渐近分析理论表明周期间隔可表示为[9,14]:

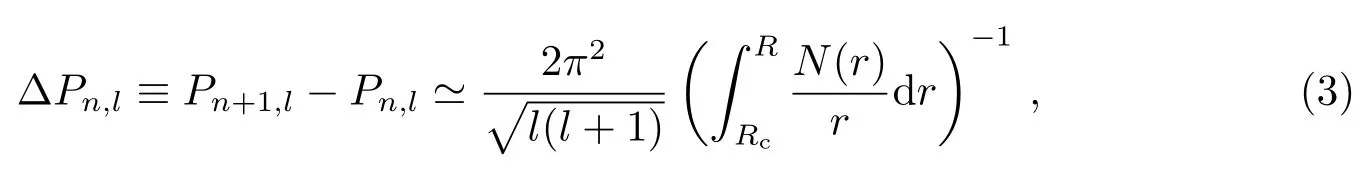
式中R和Rc分别为恒星半径和中心到对流核边界的距离,Pn和Pn+1则分别为两个连续的径向节点的模的周期.

SPB星结构上是由一个中心对流核和一个辐射平衡壳层组成的,且处在中心氢燃烧阶段.随着氢的燃烧,中心对流核在逐渐地收缩,中心氢也在逐渐地减少.那么此时在对流核边界和辐射壳层之间就必然会造成一个氢丰度梯度.图1左图中的实线显示了恒星内部氢丰度的变化,从图中能明显地看到一个陡峭的梯度.随着演化的进行,这个梯度也会变得越来越陡峭.这个逐渐陡峭的梯度也就是(2)式中的分子量梯度∇µ,这会使得N2的轮廓也同样发生变化,使其形成一个峰(见图1右图).而图中的虚线则表明了加入对流超射后对流核边界附近的氢丰度梯度的轮廓发生了变化,同时也改变了N2的峰的位置并使其轮廓变得更加平滑(见图1).

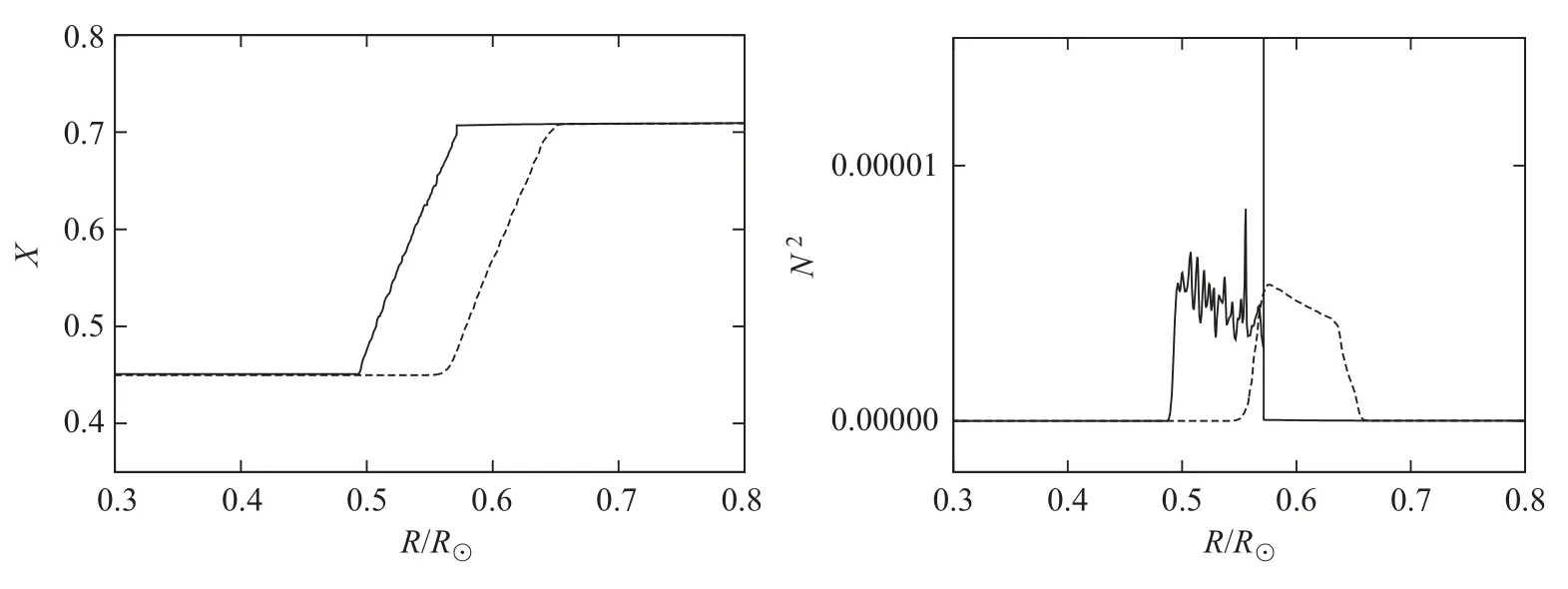
图1 恒星内部氢丰度X(左)与浮力频率(右)的比较图.实线和虚线分别为没有考虑超射和考虑指数衰减的中心对流超射的情况Fig.1 The comparison of hydrogen abundance X(left)and buoyancy frequency(right)in the interior of stars.The solid and dashed lines present the models without and with convective overshooting in the core,respectively

根据(3)式,g模的周期是近似等间距的,然而Miglio等[13]的文章中指出,收缩的对流核留下的分子量梯度会使得其振动模的周期间隔偏离常数∆P.分子量梯度引起的浮力频率的尖锐特征可能会导致共振条件,使得化学元素梯度所在的区域发生模式囚禁.

3 观测数据

根据KIC 8324482的KIC参数和其具有较长覆盖时间的光变曲线,Balona[15]将这颗星归类为γ Dor型脉动变星.但后来通过与LA参数对比以及由Kepler 4年的观测所得数据所做的频率分析,Zhang等[16]认为其KIC参数里的有效温度被低估了,并确认KIC 8324482是一颗SPB星,而不是γ Dor型变星. 根据其LAMOST光谱,Zhang等[16]给出了KIC 8324482的一些基本参数:有效温度Teff=16469±71 K,表面重力lg g=3.72±0.05,金属丰度[Fe/H]=−0.06±0.03 dex以及这颗星的径向速度vr=−18.5±2.4 km·s−1.

此外,他们还提取了这颗星的446个频率,并从中挑选出14个近似等周期间隔的模式组成了一组连续的周期序列,并认为其可能是l=1,m=0的模.表1给出了这14个模的频率fi、周期Pi以及周期间隔∆Pi.图2则给出了这组周期序列中的14个模的周期与周期间隔的分布图.在前一个工作中,通过周期间隔随周期的变化特征,我们初步确定该SPB星中心氢(Xc)大概在0.5附近.

4 计算模型

4.1 物理输入

我们在计算恒星结构与演化模型时采用的计算程序是Modules for Experiments in Stellar Astrophysics(MESA),MESA是Paxton等[17−18]在2011年公布的一个恒星演化程序模块,在本次工作中我们使用6596版本中的pluse模块来计算恒星演化模型以及它们相对应的振荡频率[17–19].

在程序计算中处理恒星内部物质混合问题时,我们采用的是Asplund等[20]给出的A09混合模型和OPAL Type 1[21]不透明度表.SPB星内部的中心对流区的对流运动是一个极其复杂的物理过程,对于怎样处理这一物理过程,我们采用了现在被广泛使用于恒星模型计算中的混合长理论(MLT)[22],且将混合长参数设置为αMLT=2.目前星震学分析表明上主序星中心对流超射不可忽略[23].对于超射区的扩散有多种近似法,在本次工作中我们采用指数衰减法来处理超射区的扩散近似.这种方法是由Freytag等[24]和Herwig[25]提出的:

其中,Dov是指超射区的扩散指数,Dconv是中心对流核内的对流混合区域的扩散指数,z=r−rc是超射区边界到中心对流核边界的距离,Hp是指局地压强标高,fov是一个可调的超射参数.

4.2 模型网格

在本次工作中,我们分别设置了3个网格来进行模型计算,它们的命名和组成如下(见表2):

网格A:我们设置其恒星初始质量Mini的范围为4–6 M⊙,步长为0.25 M⊙,初始氢丰度Xini被设置为常数0.71,初始金属丰度Zini范围从0.01到0.04,步长为0.0025.对于中心氢丰度Xc,我们的计算从0.55开始,到0.45结束,主要来源于前期准备工作中的估算.

网格B:在网格A的基础上,我们在中心对流核外边界加入了一个指数衰减超射fov,其中心对流参数fov∈[0.00,0.035],步长为0.005.

网格C:根据这颗星的周期间隔变化特征,我们认为在模型中应该加入一个不大的全局扩散,于是在网格B的基础上,我们除了缩小了对流超射系数范围以外,还考虑了全局扩散,其扩散系数被设置为lg(Dmix/(cm2·s−1))∈[1,4],步长为0.5.

表2 网格A、B和C的变化范围Table 2 The variation range of grids A,B,and C

4.3 筛选最佳拟合模型

在本次工作中,我们采用最小χ2值的方法来挑选最佳拟合模型.与Wu等[26–28]之前的工作类似,我们只采用震荡数据(即周期Pi和周期间隔∆Pi)来从每个演化轨迹中确定最佳拟合模型,即在这一过程中不考虑光谱观测数据(如有效温度Teff,表面重力lg g等).其χ2值的计算公式如下所示:

5 模型计算结果

表3分别列出了3个网格(见表2)的最佳拟合模型.表中前两列为其网格和模型编号,后6列给出了每个最佳模型的输入物理参数,最后一列为其χ2值((7)式).

表3 3个不同网格(表2)的最佳模型及其输入参数Table 3 Best models from three different grids(Table 2)and their input parameters

模型1和模型2分别是网格A和B中拟合最好的模型,对比这两个模型的χ2值,模型1明显要高于模型2,由此可见,在这颗星的对流核外边界肯定是存在对流超射的.而将模型2和模型3对比,又能看出模型3的χ2值要略低于模型2,这表明模型加入一个不大的全局扩散是有必要的.

图3将模型2的周期与周期间隔同观测进行了比对,由图中我们能看出模型2的周期与周期间隔和观测基本一致,这进一步证实了Zhang等人的猜测(这组周期序列的模式为l=1,m=0的模).图4给出了模型3的周期与周期间隔同观测的对比图.通过比较图3和图4,我们发现全局扩散使得单个模式的囚禁变强了,而对于整体的囚禁却变弱了.

图3 模型2(虚线)的周期和周期间隔分布与观测(实线)对比图Fig.3 The comparison of the period and period spacing distribution for model 2(dashed line)and observation(solid line)

另外,我们在第2节中提到模式囚禁与化学成分梯度有关.对于SPB星来说,其对流核收缩后留下的氢原子丰度的梯度,可以俘获模式并导致周期间隔的图像呈震荡分布.于是我们可以利用模型分析来了解二者之间的关系.

图5给出了一个模型(初始质量Mini=5.55 M⊙,初始化学元素丰度为(Xini,Yini,Zini)=(0.71,0.268,0.022))在4个不同主序演化时期的周期与周期间隔分布图,这4个时期分别是在其中心氢丰度为0.68、0.6、0.5和0.4时.图6中则给出了中心对流核边界附近区域这几个时期相对应的氢丰度的轮廓变化图.

图4 模型3(虚线)的周期和周期间隔分布与观测(实线)对比图Fig.4 The comparison of the period and period spacing distribution for model 3(dashed line)and observation(solid line)

图5 模型在主序阶段4个不同演化时期的周期间隔对比图Fig.5 Period spacings∆P as a function of periods P for the model during four different evolution stages

在图5和图6中,红线对应于没有加入对流超射的模型.可以看出,随着中心氢的减少,氢丰度在对流核边界附近的变化幅度增大,同时周期间隔的振荡图像的频率和振幅也在增加.图5和图6中的绿线对应于加入中心对流超射的模型,其超射参数值为fov=0.018,从图6中能看到,绿线明显相较于红线而言要更平滑些.这是由于加入对流超射后,扩大了中心对流混合区域,这使得化学丰度的变化在这个超射区域得到缓冲,从而使得氢丰度的变化曲线变得平滑.与此同时,从图5中不难看出,在加入对流超射后,周期间隔的振荡幅度明显减小了.这表明周期间隔的振荡频率与对流核边界附近的氢丰度变化幅度成正比,而周期间隔的振荡幅度则和这个地方的氢丰度变化率成正比.

图6 模型在主序阶段4个不同时期中心对流核边界附近氢丰度的轮廓.与图5相对应Fig.6 Corresponding to Fig.5,the abundances of hydrogen during four different evolution stages

图7给出了网格C的自由参数Zini、Mini、fov、lg Dmix、Xc以及半径R对应的lg χ2值的分布.由此,我们可以对KIC 8324482这颗星的一些基本参数进行精确估算.结果表明,lg χ2值在Zini没有收敛于某一特定值,但可以初步确定Mini、fov、lg Dmix、Xc和R的范围.

6 结论

在这篇论文中,我们对慢脉动B型(SPB)星KIC 8324482进行了初步的星震学分析,从分析结果中确定了这颗恒星的一些物理参数,也更加清楚了这类星内部的一些物理过程.

通过模型拟合,我们判定SPB星KIC 8324482是一颗处于主序中期(Xc=0.475–0.495)的恒星,同时还确定了这颗星的一些基本参数:M=4.8–5 M⊙、Z=0.015–0.035、R=3.4–3.8 R⊙,进一步证实了这类星的对流核外有对流超射现象.对于这颗星来说,应该在其对流核外边界加入一个超射参数为fov=0.030±0.001的指数衰减对流超射,同时,模型中还应加入一个不大但是必要的全局扩散:lg(Dmix/(cm2·s−1))≃2.

我们还对这类恒星对流核收缩所造成的分子量梯度与其振动周期间隔的关系进行了分析,得到结论:SPB星对流核收缩所留下的分子量梯度会导致其振动模式发生模式囚禁,由此引起的周期间隔的震荡与这个分子量梯度的轮廓存在关系:分子量梯度的落差与周期间隔震荡的频率成正比;而分子量变化率则和周期间隔震荡的幅度成正比.