基于低压小流量滴灌的压力流量传感器标定

2018-10-12张胜江杨鹏年

节水灌溉 2018年9期

郭涛，张胜江，杨鹏年，陈冰，段腾

(1.新疆农业大学水利与土木工程学院，乌鲁木齐 830052；2.新疆农业节水工程技术中心，乌鲁木齐 830049； 3.新疆农业大学草业与环境科学学院，乌鲁木齐 830052)

近年来随着精确灌溉概念的提出，我国农业灌溉方式正由传统的人工经验灌溉向自动化、智能化方向迈进[1-3]，其中农用型传感器是农业实现自动化灌溉的关键技术设备之一，因此对传感器的标定是农业生产过程中的一个重要环节。目前国内学者对农业灌溉系统中不同类型的传感器进行了许多研究和标定，李春林[4]通过使用土介质进行传感器的标定，建立了土压力传感器的输入与输出之间的关系。魏恒文[5]对田间作物进行高、中、低灌溉水平试验，研究作物根区各层土壤的含水率，得到了土壤水分传感器埋设深度的两个方案。唐玉邦[6]等人通过研究提出了用田间原状土对土壤水分传感器进行水分特征曲线的标定方法，降低了精确灌溉系统土壤水分测定的误差。综上所述，灌溉控制系统中传感器的标定研究主要集中在土壤水分和土体压力[10]等方面，对传感器在管道中测量压力、流量的标定研究相对较少。因此，本文主要通过试验对不同流量下传感器测得的压力、流量数据进行分析研究，并分别标定出该传感器压力、流量的输入与输出之间的关系，为低压小流量滴灌系统管道中压力、流量的测量提供一定的理论依据。

1 试验内容与方法

1.1 试验装置与设备

本试验在新疆水利水电科学研究院实验室内完成，主要设备为：流量控制平台、SIIC-F/P-P/5-5.0型压力流量传感器、压力表。试验所用的传感器是由乌鲁木齐福斯特自控系统设备有限公司提供的，相较于其他传感器，该传感器有2个信号通道，可以实时输出管道中的压力、流量信号，能够采集到压力为0～0.4 MPa，流量为0～70 m3/h的数据，适用于低压小流量滴灌(见图1)。

如图2所示，该系统的工作过程为：试验开始前先在流量控制平台1设定管道中的过水流量并启动，此时水泵通过管道(管径为90 mm)向外不断抽水，压力表显示当前流量下的压力值，RTU通过传感器会自动采集并向DTU发送一组压力、流量数据，DTU通过RS485接口与PC端相连，并将数据传输至PC端，完成数据的一次采集。其中在PC端主要是利用ModScan完成对RTU传输数据的读取，本次试验在Modscan中设置连接的端口号为COM4，波特率为38 400，RTU的ID为2，数组长度设为5位，其他为默认初始状态。

1-流量控制平台；2-电缆；3-蓄水池；4-水泵；5-压力表；6-RTU；7-压力流量传感器； 8-管道；9-天线；10-DTU；11-PC端图2 试验装置图Fig. 2 Test device diagram

1.2 试验方案

为检验该传感器运行状态的稳定性和测量数据的可靠性，故选用7个相同的传感器分别进行试验，并采集不同流量下传感器的输出压力、流量数据。其中流量共设为7个水平，分别是20、25、30、35、40、45、50 m3/h，传感器在某流量水平下的试验过程为：通过流量控制平台设定管道中的过水流量并启动，约40 min后，观察压力表和流量控制平台，当压力表的指针不摆动且流量控制平台显示的流量为设定流量，即管道中的流量稳定时，记录压力表读数和设定流量，并在30 s内记录在此流量下传感器采集到的16组压力、流量数据。

2 试验数据处理与分析

2.1 异常值的判定

采用狄克逊(Dixon)检验法[7]判定传感器测得的压力、流量数据是否存在异常值。具体检验步骤如下。

(1)分别将不同流量下各传感器采集到的16组压力、流量数据从小到大依次排列。

(2)令H=16,查阅统计计算方式表，选取对应的公式计算Q统计量，其中最小值Z(1)检验公式如式(1)所示，最大值Z(H)检验公式如式(2)所示。

(1)

(2)

(3)根据狄克逊法界外值检验的临界值表查出检验显著概率为5%和1%时，Q统计量的临界值Q0.05(H)和Q0.01(H)，两个值分别为0.546、0.627。

(4)判定：若检验最小值的计算统计量Q22≤Q0.01(H)或检验最大值的计算统计量Q22≤Q0.05(H)，则受检验的测定值正常，否则为异常值，此时剔除该数据，令H=15，重新查表并计算。经计算发现试验的各组数据均不存在异常值，即在不同流量下传感器测得的数据的离散性较低，该传感器测量的稳定性较高。

2.2 数据间差异性的分析

为了检验在不同流量下各传感器采集的压力、流量数据是否存在显著性差异，本小节主要利用SPSS软件进行单因素方差分析。通过单个样本K-S检验，各组压力、流量数据的P值均大于0.05，说明数据呈近似正态分布，则在单因素方差分析中选用Duncan法进行多组样本间差异显著性分析，结果如表1和表2所示。其中表2的压力值与表1的流量值相对应，即试验中通过安装压力表读取在此流量下管道中的压力值。表1和表2最后一行的a、b子集均为同类子集，ab为这两子集的交集，即对7个传感器测得的数据进行差异显著性分析时，当传感器之间无显著差异时，划分到同一子集，否则划分到不同的子集。

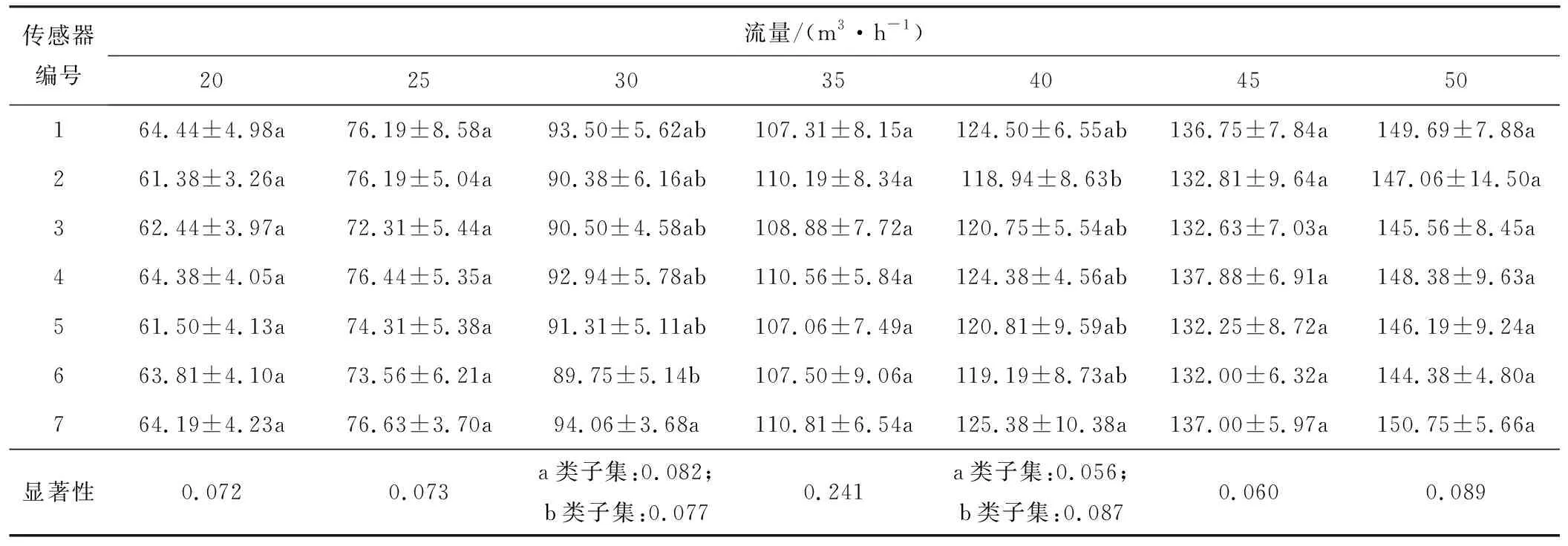
表1 不同流量下不同传感器流量数据的差异显著性Tab.1 Significant differences in flow data of different sensors under different flow rates

表2 不同压力下不同传感器压力数据的差异显著性Tab.2 Significant differences in pressure data of different sensors under different pressures

由表1可知，当流量为30 m3/h时，6号和7号传感器间呈显著差异。1、2、3、4、5号传感器之间无显著差异，6号、7号分别与这5个传感器间无显著差异；当流量为40 m3/h时，2号和7号传感器间呈显著差异，1、3、4、5、6号传感器之间无显著差异，2号、7号分别与这5个传感器间无显著差异；其他流量下7个传感器的流量数据之间均不存在显著差异。同理，在表2中，当压力为0.008 MPa时，1号和2号传感器之间存在显著差异；当压力为0.042 MPa时，6号和7号传感器之间存在显著性差异；其他压力下7个传感器的压力数据间不存在显著差异。

利用贝塞尔公式和别捷尔斯公式，对存在显著差异的传感器所在列中的所有数据进行计算，主要计算过程如下：

(3)

(4)

式中：n为数据的个数；Vi为残差。

2.3 试验数据的拟合

试验是在设定的7个流量水平下，对7个传感器测得的压力、流量数据进行了16次测量，属于大量重复试验，数据冗余，为减小试验过程中的偶然误差，故选用数据加权平均融合[11,12]的方法进行拟合，公式如下：

(5)

式中：Wi为分配给第i次检测的权数。

在表1中，当流量为30 m3/h时，b类子集的显著性低于a类，即b类子集中传感器之间的差异性小于a类子集，故选取b类子集中各传感器的原始测量数据加权平均融合，结果取整。同理，当流量为40 m3/h时，选取a类子集中传感器的原始数据加权平均融合，在表2中融合数据的选取类似于表1。对流量、压力数据加权平均融合的结果如表3所示,拟合关系特性曲线如图3所示。由图3可以看出，传感器的输出流量数据与输入流量、输出压力数据与输入压力均成正比，线性关系良好，拟合优度分别为0.996 5、0.987 2。