雷达回波外推方法在临近降雨预报中的应用
2018-10-12张卫国范仲丽江雨田孙飞飞
张卫国,范仲丽,钟 伟,江雨田,孙飞飞,陈 娟
(1.宁波市水利水电规划设计研究院,浙江 宁波 315192;2.河海大学水文水资源学院,南京 210098)
数值预报对强对流天气的临近预报技术还不够成熟,但强对流天气引发的气象灾害对民众的生命财产安全造成极大的危害。因此,对强对流天气的预警和临近预报意义重大。而雷达估测降雨在城市监测预警方面的应用将是未来水利防洪领域的前沿[1]。
天气雷达具有高时空分辨率的优势,可以快速、大范围捕捉强对流天气情况,也因此越来越多地被应用到强对流天气短时临近降雨预报中。雷达回波最优空间相关方法最早被用于Austin和Bellon[2]研究中,利用平均移动矢量对降雨进行了预报;在此基础上,Rinehart和Gravey[3]发展了TREC(Tracking Radar Echo By Correction)方法,将雷达回波分为多个区域,得到不同的移动矢量;Li[4]等在TREC基础上发展了COTREC方法,并进行了降水预报。而多数利用TREC方法的研究中,只作雷达回波位置和大概形状的外推,对回波内部的量变不作修正。
雨强的临近估计主要根据雷达回波反射率因子Z和雨强R的关系式进行。在多数研究中,该关系式中参数都采用固定参数或经验参数。但实际上,不同地区或者不同降雨过程中,参数值存在较大差别,使得雷达降雨估测与实际降雨偏差较大。因此,利用实测雨量数据对雨强关系式中参数的实时校准,以减少更多的估算误差是很有必要的。
本文以台风多发的宁波市为例,利用给定研究区的雷达回波最优空间相关方法,得到前一时次每6 min的雷达回波移动矢量,对该矢量的2个分量分别利用最小二乘回归得到其与时间的关系,由此可得下一时次的移动矢量;叠加上一时次雷达回波内部变化量后,得到雷达回波预报图像,实现对雷达回波位置、形状的外推及内部回波量的修正。对Z~R关系式进行变形,采用SCE-UA算法对雷达回波强度N与降雨强度R关系中参数进行估算与实时校准,尝试预测下一时次的降水分布情况。
1 理论方法
本文采用给定研究区的雷达回波最优空间相关方法对强对流天气下雷达回波的位置和形状进行外推,并把上一时次的雷达回波变化网格叠加到下一时次的雷达回波预报中,得到最终的雷达预报图像。根据雷达反射率因子与雨强的关系式的变形公式对雨强进行估算,利用SCE-UA算法对雨强关系式中参数进行实时校准,得到时效性较好的A,b参数,从而得到相对准确的下一时次预报降雨分布。
1.1 雷达回波最优空间相关方法
从雷达回波图像上可以看出,雷达探测回波存在明显的、较为明确的移动轨迹(见图1)。根据已发生的短时间内的雷达回波移动轨迹,推测下一时次雷达回波的位置及形状,即是雷达回波最优空间相关方法的核心思想。
雷达回波最优空间相关方法,是在假设大气中水汽的移动受环境风场的引导,而环境风场在短时间内不存在严重突变的前提下成立的。将已探测到的雷达回波的移动矢量作为当前环境风的移动矢量,来预测未来短时间内雷达回波的移动矢量。该方法简便,运算量小,运行时间短,在有大面积层状云时跟踪效果较好[5]。
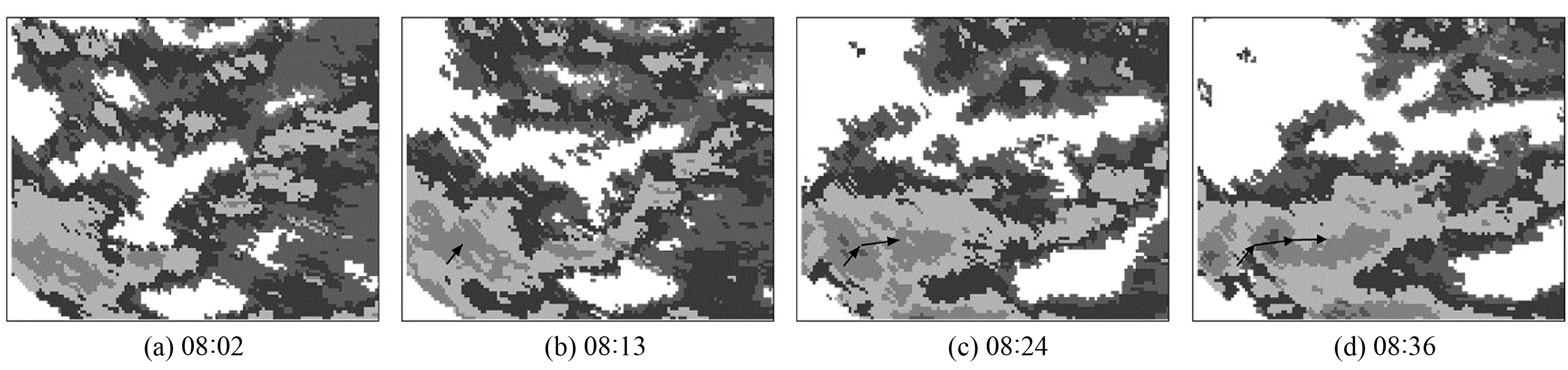
图1 雷达回波移动轨迹示意图(2018年4月4日)Fig.1 The schematic of radar echo movement track (April 4, 2018)
给定研究区的雷达回波最优空间相关方法具体步骤是,将整个回波区域按照研究区的网格大小划分成若干个相同大小的矩形网格,研究区雷达回波矩形网格与上一时刻的若干矩形网格之间计算相关系数,寻得的最大相关系数的网格到研究区网格对应的矢量即为该天气系统下相邻时刻雷达回波的位移矢量。
相关系数R的计算公式如下:
(1)
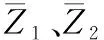
寻找与研究区网格最大相关系数的网格时,为缩减计算矩形网格的数量,可根据雨带移动的最大期望速度与分析时间间隔得到最大网格搜索半径。为减小网格距离计算量,可采用最大网格搜索半径为边长的正方形作为搜索区域。按网格大小为一个移动单位进行移动,求得在最大搜索半径范围内的所有网格(计算区)与下一相邻时次研究区网格的相关系数。其中相关系数最大的计算区网格中心到研究区网格中心的矢量即为t1到t2时刻的位移矢量(见图2),并保存该计算区网格与研究区网格的变化量网格E。重复寻找当前时刻之前一定时间段内相邻时次的雷达回波图像的位移矢量(Δx1,Δy1),(Δx2,Δy2),…,(Δxn,Δyn),记录一系列变化量网格(E1,E2,…,En)。假设环境风场方向及风速在一定时间段内稳定,可以分别建立X方向与Y方向上的位移分量Δx、Δy与绝对时间t之间的线性关系式:
Δx=a1t+b1
(2)
Δy=a2t+b2
(3)
根据至少2组数据[t1,(Δx1,Δy1)],[t2,(Δx2,Δy2)]即可确定a1、b1、a2、b24个参数,理论上可用来计算未来任意时间与其相邻前一时次间的雷达回波位移矢量。在实际运用时,需要考虑方法的时效性。

图2 给定研究区的雷达回波最优空间相关方法Fig.2 Radar echo optimal spatial correlation method for a given study area
在确定雷达回波外推位置与形状后,叠加上一时段的变化量网格,可以得到最终的外推雷达回波图像。
1.2 SCE-UA算法
复合形交叉进化算法(SCE-UA)是一种全局优化算法,集成了随机搜索算法、单纯形法、聚类分析法等方法的优点,是一种有效解决非线性约束最优化问题的混合算法[6,7]。该算法引入了种群的概念。复合形点在可行域内随机生成、竞争演化,在多个吸引域内获得全局收敛点,能有效地表达参数敏感性与参数之间的相关性。SCE-UA算法基本思路是首先在参数可行域内引入随机分布的点群,将其分为多个复合形,每个复合形中有2n+1个点(其中n是需要优化的参数个数);每个复合形根据下降单纯形算法进行进化;定时地将整个点群混合进而形成新的复合形,也就将之前的复合形所包含的信息引入新的复合形中;进化与混合不断进行直至满足收敛准则[8,9]。
SCE-UA算法中大部分参数取值可以采用默认值:

(4)
式中:n为参数个数;m为每个复合形的顶点个数;q为每个子复合形顶点个数;s为种群大小;α、β为父辈产生的子辈个数与代数;p为复合形个数,需根据具体情况确定。
该算法流程见图3。

图3 SCE-UA算法流程Fig.3 SCE-UA algorithm flowchart
2 应用实例
本文选取台风多发的宁波市为研究区,区内汛期期间(4-10月),受台风和热带风暴登陆侵袭,造成全流域或部分流域的强降雨,降水量较大。
2.1 数据准备
宁波天气雷达基站位于慈溪市达蓬山,站点高程454.4 m。基站为CINRAD/SA系列雷达,空间分辨率为1 500 m,时间分辨率为5~6 min。本文在进行去噪、地物回波等预处理后,插值成1 km栅格以供雷达回波图像外推使用。
本文中选用于实验的雷达回波图像为2015年21号台风“杜鹃”期间2015-09-30,11∶00-12∶00,1 h内12张雷达回波图像中大于25 dBZ的区域。雷达回波区域为宁波雷达站附近350 km×380 km范围区域,研究区选取宁波市附近250 km×230 km范围区域(见图4)。
从宁波市水文站收集所需的宁波全市63个国家雨量站点5 min降雨数据,以供对预测雨强的精度分析使用。

图4 雷达回波区域及研究区示意图Fig.4 The sketch map of Radar echo area and study area
2.2 考虑雷达回波形变与量变的外推预报
本文采用的外推方法是一种线性外推算法,不考虑雷达回波在移动过程中的非线性变化、垂直运动、强度演变等。因此,若外推时间太长,则此方法外推就没有太大意义。在强对流天气条件下,60 min内雷达回波位置和形状的外推预报具有一定的物理意义和可靠性,其结果具有较好的指示意义。本文考虑60 min的雷达外推时间。同时,雷达回波强度大于25 dBZ时,具有良好聚拢效果,有明显的外廓边界,更有利于雷达回波外推。因此,本文采用前1 h内12张雷达回波图像中大于25 dBZ的区域,分析并外推下1 h的雷达回波形状及位置,利用Python语言实现图像批处理及相关计算。
雷达外推的具体过程如下:首先裁剪出宁波雷达基站附近350 km×380 km的雷达回波区域作为雷达外推的搜索区域及宁波市附近250 km×230 km范围的研究区;以图像每一个栅格大小为移动单元依次平移,用250 km×230 km裁剪窗口依次裁剪搜索区域内雷达回波图像,每张雷达回波图像搜索区域内共有100×130张裁剪出的雷达回波图像以待计算(称为计算窗口图像);计算裁剪出的所有计算窗口雷达回波图像与下一张图像中研究区雷达回波图像的相关系数(见表1、表2);保存与下一张研究区雷达回波图像相关系数最大的计算窗口雷达回波图像(见图5、图6),记录该计算窗口网格中心到研究区网格中心的X方向与Y方向2个矢量(北为Y的正方向,东为X的正方向,反之则为负);计算并记录研究区雷达回波图像与相关系数最大的计算窗口雷达回波图像的回波强度变化量网格E;得到1 h内12张雷达回波图像中前11张图像的X方向与Y方向2个移动矢量序列[(Δx1,Δy1),(Δx2,Δy2),…,(Δx11,Δy11)](见表3);叠加1 h内前11张回波图像的回波强度变化量网格∑E,作为下1 h预报雷达回波图像形状的依据。

图5 与11∶06研究区雷达回波(彩色图像)相关系数 最大的11∶00雷达回波(黑色轮廓)Fig.5 The radar echo of 11∶00 having largest correlation coefficient with the echo of 11∶06 in study area
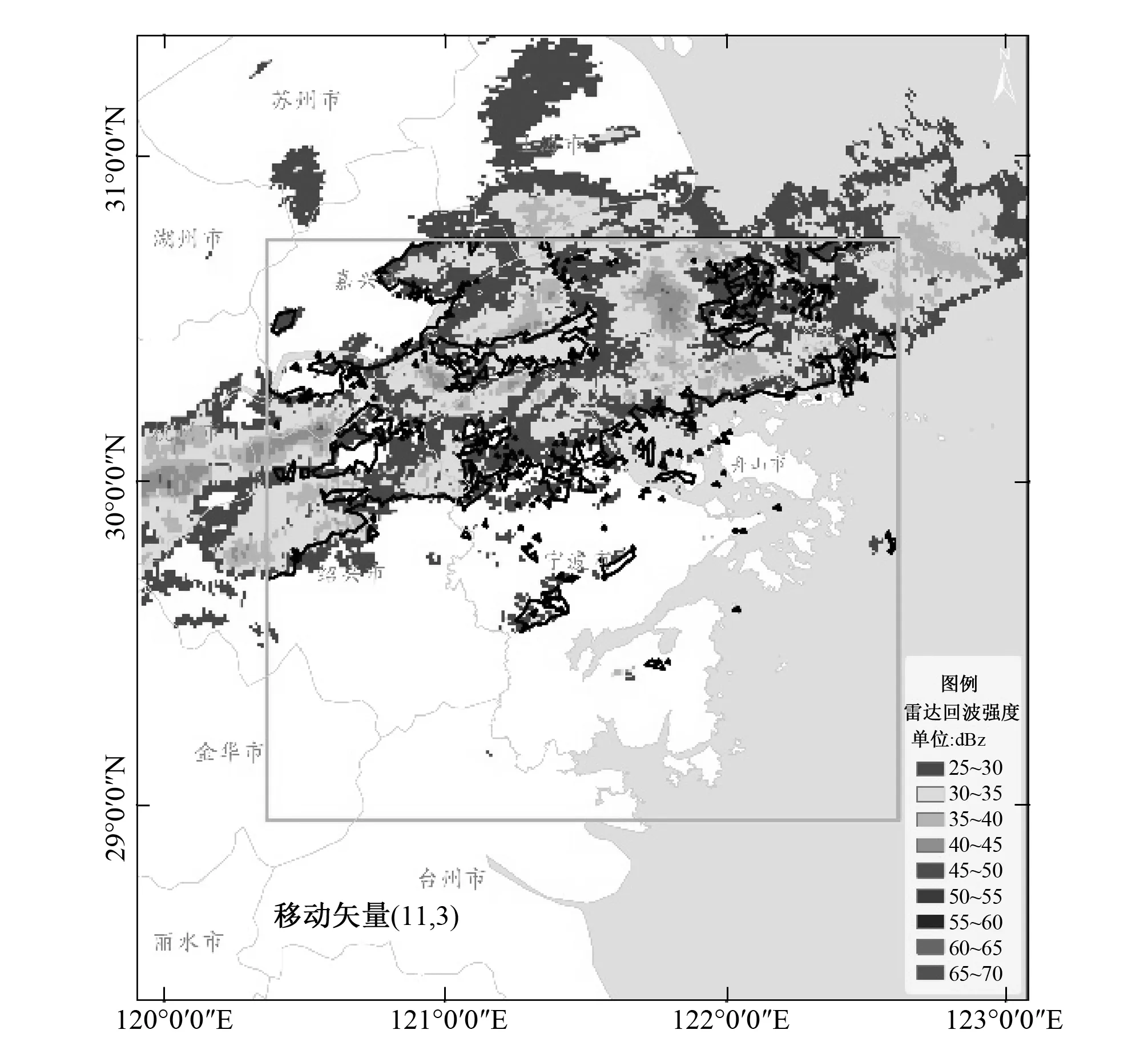
图6 与11∶12研究区雷达回波(彩色图像)相关系数 最大的11∶06雷达回波(黑色轮廓)Fig.6 The radar echo of 11∶06 having largest correlation coefficient with the echo of 11∶12 in study area
将时间换算成时间戳形式,利用最小二乘算法建立X、Y分量累积量与时间的关系式(即以11∶00雷达回波图像为准,各时间点的X、Y方向偏移量Δx、Δy):
Δx=273.5t-1 247.3R2=0.999 6
(5)
Δy=628.43t-286.21R2=0.993 5
(6)
将13∶00转换为时间戳形式,代入以上2个关系式中,得到13∶00雷达回波相对11∶00时的X、Y偏移量,该偏移量减去12∶00雷达回波相对于11∶00的X、Y偏移量,可得到13∶00雷达回波相对于12∶00的X、Y偏移量(114,26);在12∶00雷达回波区域寻找(114,26)偏移量的相反方向窗口,即为13∶00研究区窗口的雷达回波位置;在该雷达回波窗口基础上,叠加11∶00-12∶00的回波强度变化量网格E,即研究区内13∶00的雷达外推预报图像。
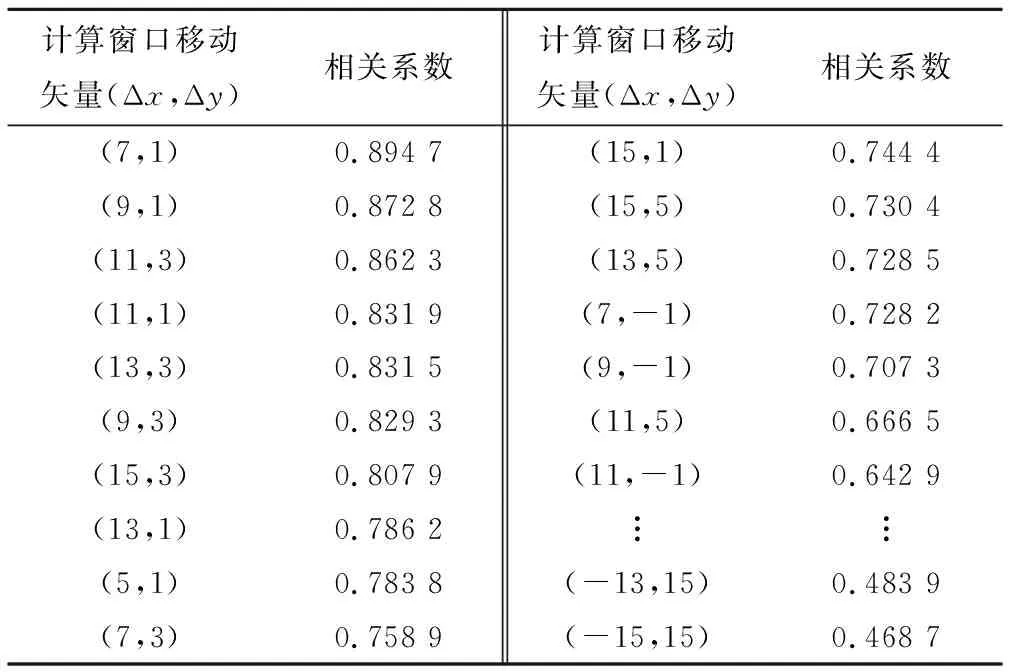
表1 11∶06研究区雷达回波与11∶00各计算窗口 的相关系数(由高到低)Tab.1 Correlation coefficient of the radar echo of 11∶00 in study area and each calculation window of 11∶06

表2 11∶12研究区雷达回波与11∶06各计算窗口 的相关系数(由高到低)Tab.2 Correlation coefficient of the radar echo of 11∶06 in study area and each calculation window of 11∶12
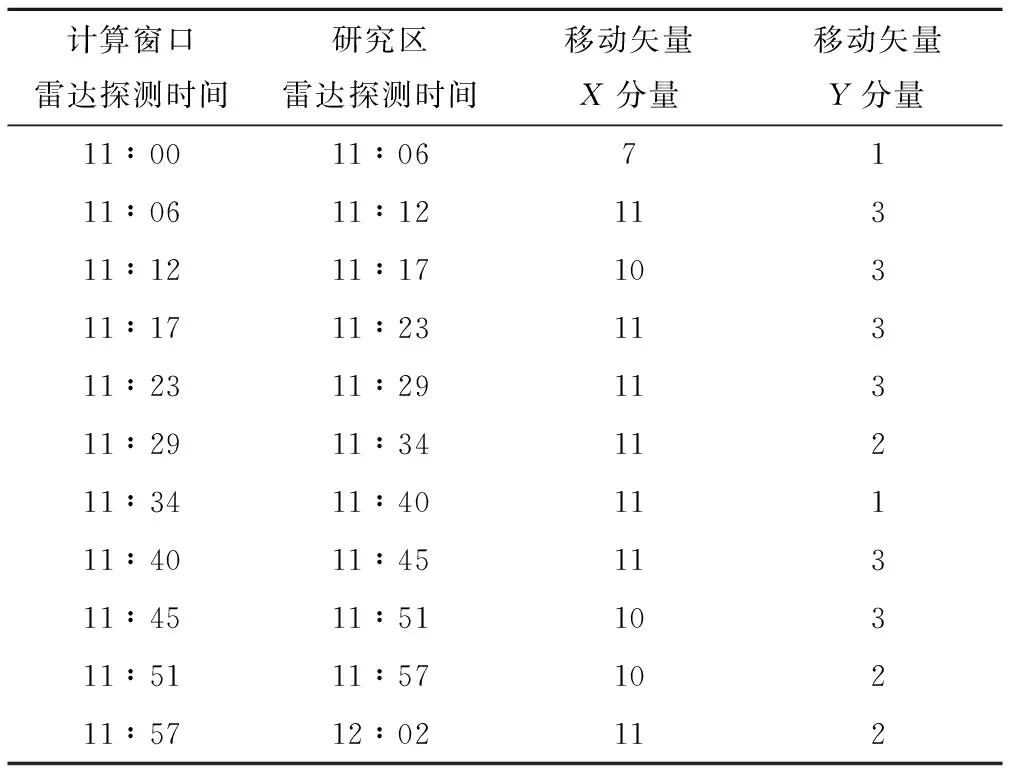
表3 2015-09-30 11∶00-12∶00 前11张雷达 回波图像移动矢量序列(Δx,Δy)Tab.3 The first 11 radar echo image motion vector sequences of 2015-09-30 11∶00 to 12∶00
由图7可以看出,考虑了雷达回波的移动过程及内部量变的雷达外推预报图像与回波实况接近,且该方法运算简便、迅速,具有较高的实用价值和可操作性。
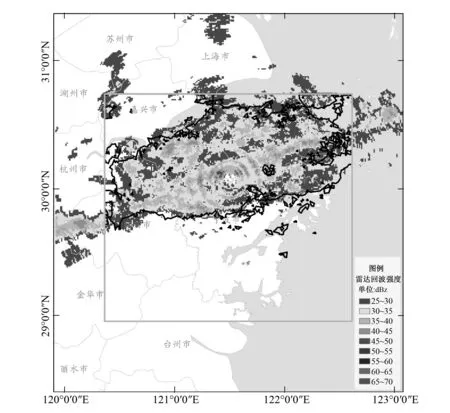
图7 2015-09-30 13∶00的60 min雷达外推 预报图像范围(黑色轮廓)及实况(彩色图像)Fig.7 60 min Radar extrapolation forecast image range (black outline) and actual image (color image) of 13∶00 on Sept 30,2015
2.3 临近降雨预测
雨量站每5 min一次实测降雨资料,按雷达探测时间整理成雨强数据。根据雷达反射率因子Z和降雨强度R的关系式Z=ARb及雷达反射因子Z与雷达回波强度N的关系式N=10 lgZ可知:
(7)
式中:A、b为待确定参数。
由这2个参数来确定雷达回波强度N和降雨强度R(单位:mm/h)的关系。本文对A,b2个参数用以下2种方法进行估算。
(1)Lemon[10]提出考虑2种对流类型给定参数:①大陆强对流型,A=300,b=1.4;②热带型,A=230,b=1.25。本文采用大陆强对流型参数,利用雷达回波预报图像,计算出预报降雨强度,用2015-09-30 13∶00降雨预报数据中有效雨量站点实测数据及预报数据求得相关系数为0.56,均方根误差δ为9.35。
(2)SCE-UA算法可以有效、快速地搜索到参数全局的最优解。为提高收敛速度,避免陷入局部最优解,需给优化参数设置上下限,建立其寻优区间。式(7)中2个参数取值范围为:A∈[200,350],b∈[0.7,1.8],作为参数寻优的上下边界。
参数优化时样本点需按目标函数值进行排序。本文构造目标函数,为降雨实测值与参数优化后的关系式计算所得估计值的残差平方和最小:
(8)
式中:Ri为降雨强度的实测值,mm/h;n为样本数量,i=1,2,…,n。
将样本数据代入式(7)中,在满足目标函数的情况下,采用SCE-UA算法优化参数A,b。算法中复合形个数p是唯一需要确定的参数,本文p取值2,则m取值5,q取值3,α为1、β为5。算法终止条件主要从3方面控制:①迭代次数10次,容许值为0.1%;②最大循环次数10 000 次;③参数收敛值为0.001。
利用SCE-UA算法对雨强与回波强度关系式进行参数估计,对60 min雷达外推预报成果进行临近降雨预报;利用雨量站实测数据进行误差分析计算,以均方根误差作为衡量指标。δ的计算公式如下:
(9)
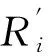
本文采用11∶00-12∶00实测降雨资料及雷达回波强度数据,得到参数A=318,b=1.12。用13∶00降雨预报数据中有效雨量站点实测数据及预报数据(见图8)求得相关系数达到0.85,均方根误差δ=2.48(见表4)。
事实上,A,b2参数对降雨预报精度的参数敏感性很高,尤其b参数的选取,对预报降雨精度影响很大。因此,对不同场降雨事件的A,b参数的率定是很有必要的。
3 结 语
给定研究区的雷达回波最优空间相关方法对雷达回波位置和形状进行30~60 min的外推预报,雷达外推预报图像与回波实况接近,具有一定的可行性和可靠性。在降雨预报方面,采用SCE-UA算法估算参数的预报精度明显比采用经验参数的预报精度高,均方根误差δ=2.48(见表4),不同场降雨事件应率定相应的参数。
□

图8 2015-09-30 13∶00 实测雨强与雷达外推预测雨强Fig.8 Measured and radar extrapolation forecast rain intensity at 13∶00 on Sept 30,2015
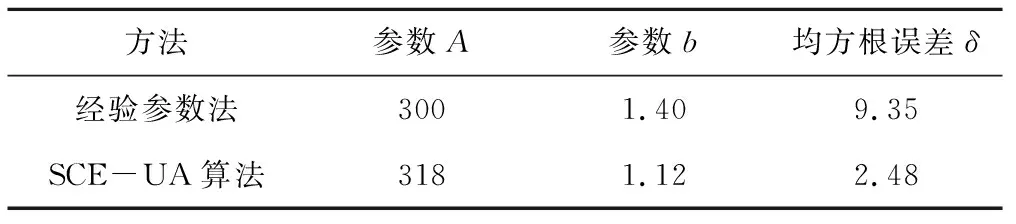
方法参数A参数b均方根误差δ经验参数法3001.409.35SCE-UA算法3181.122.48
