论线性系统的反共振问题
2018-10-11胡海岩
胡海岩
(北京理工大学宇航学院 飞行器动力学与控制教育部重点实验室, 北京 100081)
引言
早在19世纪末,人们就发现两自由度线性系统会呈现反共振现象,即系统某个自由度在特定频率激励下的稳态振动幅值为零.1902年,Frahm基于对反共振的认识发明了动力减振器,降低轮船在海浪作用下的晃动[1].此后,人们成功利用反共振现象来改善隔振系统和振动机械的动态特性[2,3],通过反共振现象来提高模型修正效果[4].近年来,则将反共振概念引入到声学超材料的设计中[5].
虽然不少学者致力于研究反共振,但主要关注反共振频率计算、反共振频率的灵敏度计算等问题[6-8],对反共振现象的机理阐述还不够透彻.例如,对简谐激励下的单自由度阻尼系统(简称主系统)附加单自由度无阻尼系统(简称次系统),当激励频率与次系统固有频率重合时,主系统完全静止,导致激励对组合系统做功为零.但有些学者认为,此时次系统吸收了主系统的振动[9],主系统的能量转移到次系统[10].即次系统的振动能量来自主系统,亦即激励输入的能量;这无疑与激励做功为零相矛盾.本文试图澄清这类矛盾,阐述原点反共振、跨点反共振的机理差异,以及反共振与固有振型节点之间的关系.为了简洁起见,本文着重研究两自由度线性系统的反共振问题.
1 两自由度系统的反共振问题
考察两自由度线性时不变系统的受迫振动问题:

(1)

通过单边Fourier变换,将方程(1)表示为频域形式:
Z(ω)X(ω)=F(ω),ω∈[0,+∞)
(2)
其中:


Z(ω) ≡K+iωC-ω2M

(3)

由式(2)和式(3)可得到系统的频域响应:
X(ω) =Z-1(ω)F(ω)

≡H(ω)F(ω)
(4)
其中H(ω)≡Z-1(ω)∈2×2是频响函数矩阵(又称动柔度矩阵).鉴于反共振是系统局部行为,对于不同的激励位置和响应测量位置,反共振频率一般不同,故将在s位置激励和在r位置测量响应获得的反共振频率标记为ωrs,r,s=1,2.
不失一般性,考察仅对系统第1个自由度施加简谐激励的情况,即F1(ω)≡F1且F2(ω)≡0.此时,若存在频率ω11使Z22(ω11)=0且Z12(ω11)≠0,则原点频响函数H11(ω11)=0,即原点响应出现反共振Y1(ω11)=0;而跨点响应为Y2(ω11)=H21(ω11)F1=-F1Z12(ω11)/detZ(ω11)≠0.若有频率ω21使Z12(ω21)=0且Z22(ω21)≠0,则跨点频响函数H21(ω21)=0,即跨点响应出现反共振Y2(ω21)=0;而原点响应为Y(ω21)=H11(ω21)F1=F1Z22(ω21)/detZ(ω21)≠0.若仅第2个自由度受到激励,也可获得与上述分析结果类似的结论.
2 反共振现象的力学机理
2.1 原点反共振问题
对于系统原点响应X1(ω11)=0这种反共振现象,许多文献用“动力吸振”概念来解释.例如,文献[9]认为:系统第2个自由度吸收了系统第1个自由度的振动.由此可推断,系统第2个自由度的振动源自系统第1个自由度的振动,其能量来自外激励F1(ω11)输入到系统第1个自由度的能量.这正是文献[10]所阐述的“能量转移”观点.以下分析将表明,上述观点并不正确.


(3)在系统原点响应达到反共振状态前,外激励向系统输入能量;当达到反共振时,外激励维持跨点响应振幅.事实上,在系统原点响应达到反共振状态之前的瞬态响应阶段,外激励在系统第1个自由度上做功,向系统输入能量.该能量激发起系统第2个自由度作不耗能的振动,产生弹性恢复力抵消外激励对第1个自由度的作用.随着第1个自由度振动衰减,外激励做功趋于零.但根据跨点响应的表达式X2(ω11)=-F1Z12(ω11)/detZ(ω11)可知,跨点响应所呈现的简谐振动幅值要靠外激励来维持.此时,若降低外激励力幅值,系统会再次经历瞬态阶段,第2个自由度的振动幅值会降低,直至重新达到动力平衡,形成稳态的反共振.特别的,若F1→0,必导致X2(ω11)→0.
以上分析表明,现有文献中的“动力吸振”、“能量转移”观点并不正确,而基于动力平衡分析所得到的“动力减振”观点更为恰当.
2.2 跨点反共振问题
对于系统跨点响应X2(ω21)=0这种反共振现象,尚未见有文献讨论其力学机理.事实上,跨点反共振现象与原点反共振现象的力学机理有所不同.此时,外激励通过第1个自由度向系统输入能量,导致第1个自由度发生受迫振动,但输入的能量无法传递到第2个自由度上.
更进一步看,跨点反共条件是存在频率ω21使Z12(ω21)=0,进而导致跨点频响函数H21(ω21)=0.这可理解为系统两个自由度之间的阻抗无限大,能量传输被阻止了.
(1)系统同时存在惯性耦合m12和弹性耦合k12,在外激励频率达到ω21时这种耦合被抵消了,外激励通过第1个自由度向系统输入能量,但该能量无法传递到第2个自由度.
(2)系统仅存在惯性耦合m12,当ω21=0时该耦合消失,即静态外激励引起第1个自由度运动,而第2个自由度保持静止.
(3)系统的两个自由度之间不存在任何耦合,外激励只引起第1个自由度振动.
3 案例分析

图1 两自由度系统及其固有振型Fig.1 A system of two degrees of freedom and its natural mode-shapes
考察图1所示的两自由度线性系统,其中均质刚性杆AB的质量为m=6,长度为ηL,其中η≥1是无量纲系数;两个弹簧的距离为L,刚度为k1=k2=1,质量可忽略不计.现取图1杆端部向上位移xA和xB为广义坐标.在这组广义坐标描述下,系统的动能和势能分别为:
(5)
由此可得到系统的质量矩阵和刚度矩阵:

(6)
3.1 固有振动
对于不同的η2取值,求解广义特征值问题:
(K-ω2M)φ=0
(7)
得到如下三种固有振动:

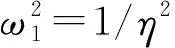

3.2 反共振频率
系统频响函数矩阵为:
H(ω) =(K-ω2M)-1
(8)
根据式(8),可得到原点和跨点频响函数的反共振频率分别满足:
(9)
参考3.1节对固有振动的讨论,可绘制图2所示的系统固有振动频率平方和反共振频率平方关系.

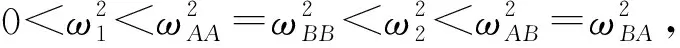


(10)
易见,此时没有反共振现象.
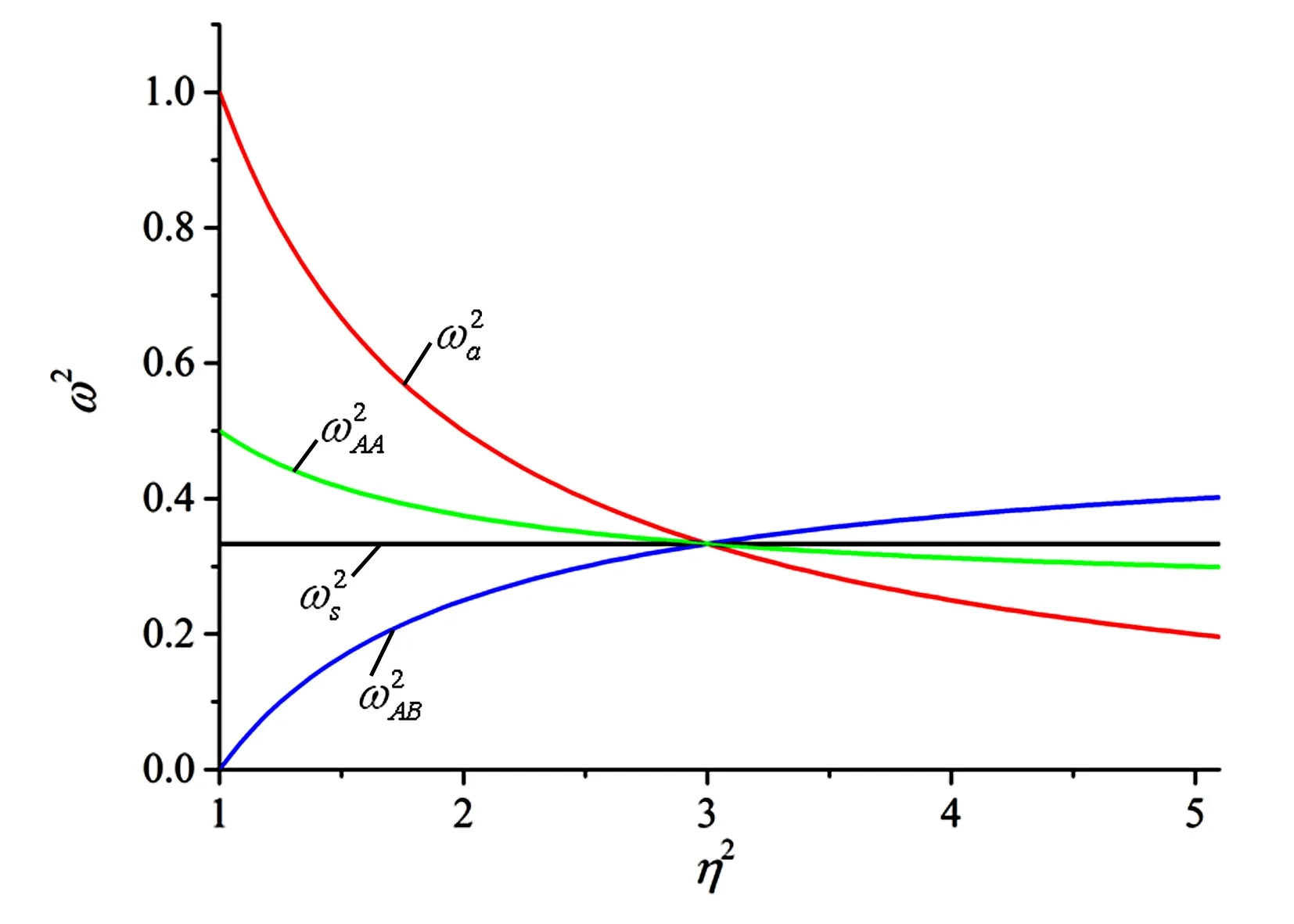
图2 对称振动固有频率平方反对称振动固有频率平方原点反共振频率平方和跨点反共振频率平方随η2的变化.Fig.2 Variations of the natural frequency of symmetric vibration, the natural frequency of anti-symmetric vibration,the anti-resonant frequencies and with an increase of η2
3.3 刚性杆上任意点的反共振
在刚性杆左端点施加沿xA正向的正弦激励fA(t)=FAsinωt,根据式(4)得到刚性杆两端的频率响应向量:

(11)
为考察刚性杆上任意点s处的频率响应,引入无量纲参数ξ=s/ηL∈[0,1],则点s处的频率响应为:
Xs(ω) =[(1-ξ)XA(ω)+ξXB(ω)]
(12)
在点s处产生位移反共振的条件是,存在频率ωsA≥0使得:
(1-ξ)(η2+1-4η2ω2)+ξ(2η2ω2+1-η2)=0
(13)
若指定无量纲位置坐标ξ,则反共振频率ωsA满足:
(14)
当η2<3时,图3(a)给出反共振频率ωsA与无量纲位置坐标ξ的关系;当η2>3时,该关系如图3(b)所示.


图3 刚性杆上任意位置ξ处的反共振频率ωsAFig.3 Anti-resonance frequency ωsA of the rigid beam at the location coordinate ξ

对于指定的无量纲位置坐标ξ,由式(14)得到该点产生反共振的频率
(15)
以下分别讨论原点反共振和跨点反共振问题.

b. 当ξ>0时,Xs(ω)成为跨点响应,其反共振频率由式(15)给出.特别当ξ=1/2时,反共振频率为ωsA=ω2=1,而ξ=1/2正是系统第2阶固有振型的节点.此时,刚性杆在左端简谐激励fA(t)=FAsint作用下发生第2阶共振,呈现绕刚性杆质心的转动.事实上,若跨点反共振频率与系统某阶固有频率重合,则反共振位置必然是该阶固有振型的节点.

4 结语
本文分析简谐激励下两自由系统的反共振问题,主要结论是:当系统出现原点反共振时,外激励对系统不做功,系统跨点响应是能量守恒的简谐振动,但其幅值要靠外激励来维持;当系统出现跨点反共振时,外激励对系统做功,但系统两个自由度之间的阻抗无限大,导致能量无法传输.对于原点反共振的力学机理解释,现有文献中的“动力吸振”、“能量转移”等观点均存在问题,建议采用基于动力平衡分析得到的“动力减振”观点.
文中通过由两个相同弹簧支撑的刚性杆的简谐受迫振动来说明上述概念,展示了丰富的跨点反共振现象.例如,在杆左端施加简谐激励、右端测量稳态振动时,跨点反共振频率可出现在低于第1阶固有频率的任意频率处,也可出现在高于第2阶固有频率的一个频段内.又如,在杆左端施加简谐激励时,跨点反共振可出现在从杆左端到杆长2/3间的任意位置上.再如,当跨点反共振频率与系统某阶固有频率相重合时,反共振位置就是该阶固有振型的节点.
