喷流噪声半经验预测模型程序设计

赵雯，毛东兴，姜在秀，邱昇，英基勇



喷流噪声半经验预测模型程序设计

赵雯1，毛东兴1，姜在秀1，邱昇2，英基勇2

(1. 同济大学声学所，上海 200092；2. 中国航发商用航空发动机有限责任公司，上海 200092)

基于喷流混合噪声半经验预测方法TA理论模型，设计了喷流混合噪声半经验预测模型程序。其中流场计算通过商用软件ANSYS，如ICEM和FLUENT实现，声场计算通过Fortran90代码编译完成，仿真计算得到的喷流噪声远场声压级与Tam等人的实验数据吻合较好。同时提出了一种简化计算方法，在保证计算结果准确性的前提下，明显提高了计算速度。

喷流噪声；半经验；TA模型

0 引言

Lighthill[1-2]是气动声学的开拓者，他在最初的声类比理论中将喷流噪声声源类比成四极子声源的形式。但是简单地用声类比方法表示声源导致其只能局限在特定的理想条件中应用。1972年，Lilley等[3]提出将表示声流相互作用从声源项转移到传播算子中，改进了Lighthill理论在折射效应等声流相互作用中的局限性。基于Lighthill方程和Lilley方程的方法，通常统称为声类比法，声类比法代表模型有(Mani-Gliebe-Balsa, MBG)模型[4]及Khavaran对其修正得到的MGBK模型[5]等。

本文基于TA模型，通过商用软件ANSYS对流场进行仿真计算，提取出相关的平均流和湍流参数信息后，进行声学网格划分和插值，再通过编写Fortran90代码，对远场喷流声场进行数值计算，并提出一种简化的计算方法，在保证准确性的前提下，明显提高了计算速度。

1 理论模型

TA理论模型以线性欧拉方程为控制方程，声源项以浮动轴向速度分量的时空相关函数的数学表示进行建模，声传播项以伴随格林函数的方法进行求解。相对于传统的格林函数，伴随格林函数极大地减少了计算复杂度，且无频率假设，相对于MGBK等声类比方法，能够得到与实验数据更为相符的计算结果。

1.1 声源模型

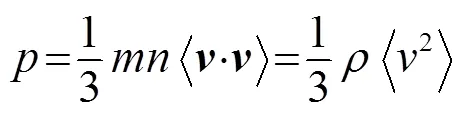
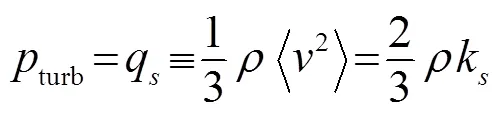
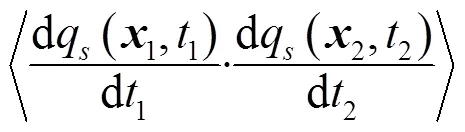
1.2 声传播模型

TA模型中对声传播项的求解是通过伴随格林函数的方法进行的[10]。传统格林函数的求解问题即为计算趋于无穷多个具有奇异点的方程问题；而伴随格林函数基于互易定理，将声源点和声接收点互换位置，此时所需考虑的奇异点只有一个，因此伴随方法可以明显降低计算过程的复杂度。同时伴随格林函数的求解无需做频率近似的假设，提高了计算结果的适用范围和可信度，使声场计算结果在较宽频带内与实验数据吻合较好。

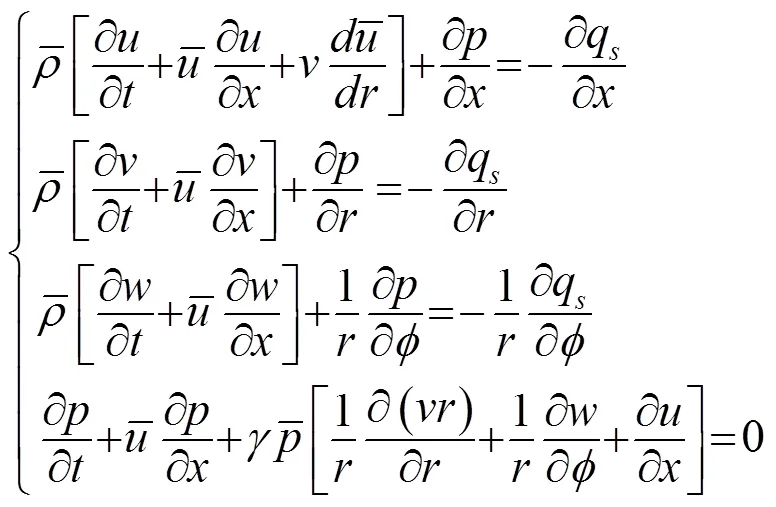
通过推导得到满足互易关系的伴随格林函数组表示为(下标表示伴随参数)

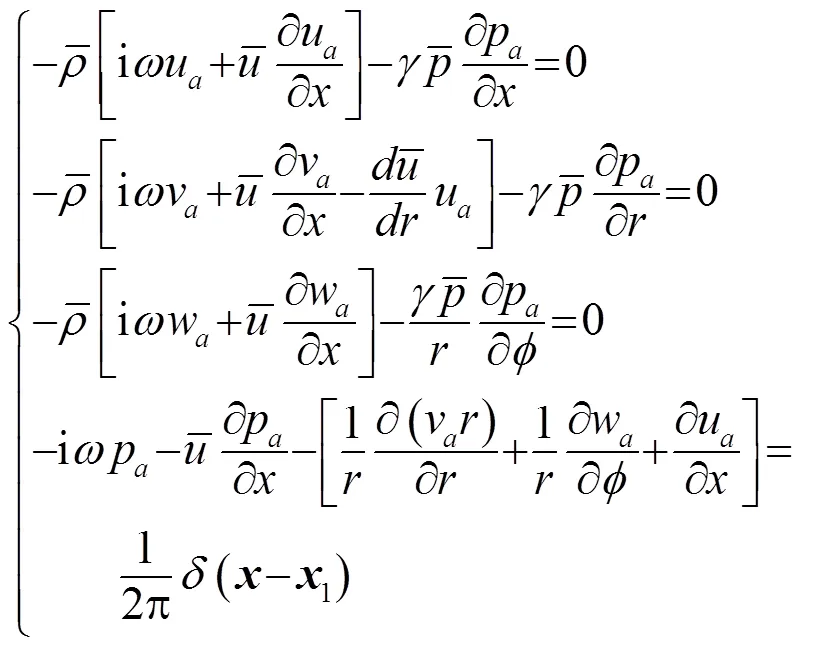
方程(6)的解可用入射平面波及散射波来表示，将平面波按柱面波展开后，其散射波解可依据分离变量法来确定。

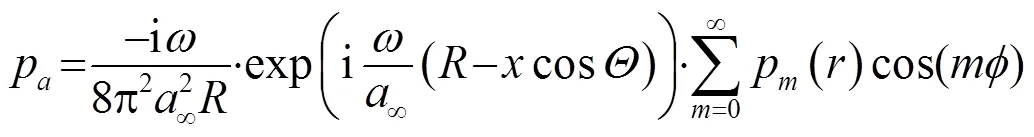
根据维纳辛钦定理，功率函数可表示为

2 仿真计算

首先通过流场计算软件计算得到相应的平均流和湍流参数，然后经过声学网格的划分和插值，最后即可通过Fortran90编写声场计算代码。

2.1 流场计算

流场计算中使用的几何模型为圆直口喷口，喷口几何信息如图1所示。

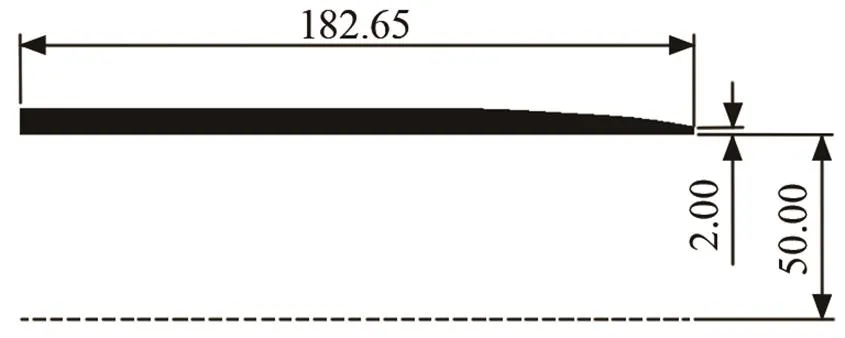
图1 轴对称喷流喷口几何模型(mm)

流场计算是通过商用软件ANSYS实现的，网格划分无特殊要求，建议进行网格无关性验证。本文采用ICEM进行结构网格划分，左右端采用无反射边界层处理方法。计算域共有90 575个网格，轴向距离范围为(-1.1，10)，径向距离范围为(0，1)，单位：m。其中，=0为对称轴。网格最小面积为10-4m2。

求解公式采用隐式算法和Roe-FDS通量格式，对流项离散采用二阶迎风格式，且计算收敛残差至少为10-4。另外，建议增加两个监视器窗口，迭代计算结束时需确保出入口处质量流量达到稳定。

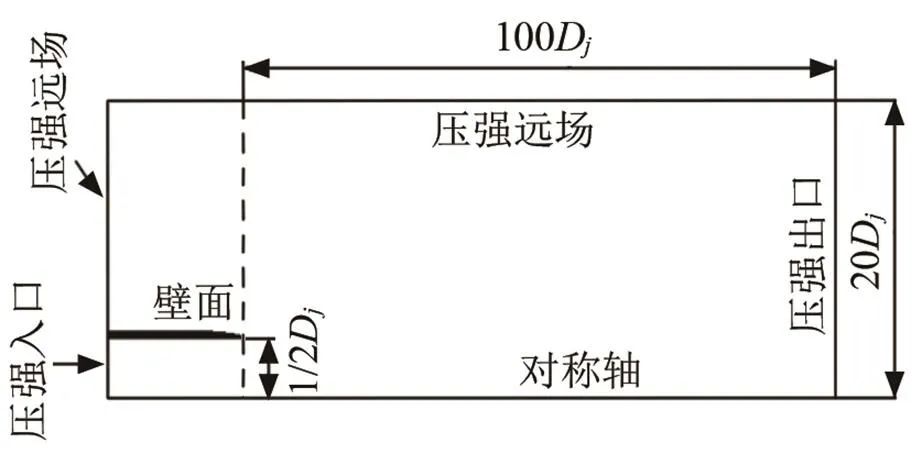
图2 流场计算域示意图

2.2 声场计算

从流场中导出相关的平均流参数和湍流参数，进行声学网格的划分及插值，由此得到均匀分布的网格节点及插值后对应的流场数据。代入编写的Fortran90程序中，进行声场计算，可得到声场计算结果。其中，式(8)伴随格林函数中分离变量得到的距离函数满足的二阶常微分方程用四阶龙格库塔格式求解，流场参数的梯度用中心差分的方法表示。在利用差分求流场参数径向导数时，二阶导数会出现振荡，通常先对流场进行过滤后再求导[11]。但是计算结果表明，是否进行过滤对最后的声场结果影响很小，同时为了提高计算效率，本文未进行过滤操作。声场计算中用球坐标表示声场观测点位置，该球坐标系如图3所示。

图3 观测点坐标系示意图

2.3 简化方法

伴随格林函数的思想是基于互易关系，在自伴随条件下，声源点位于远场，接收点位于喷流内，此时在接收点处接收到的直达声可近似表示为平面波，为推进后续计算，须将直达声表示为无穷多阶柱面波的叠加，显然，合理的柱面波阶数不仅有利于保证声场计算结果的准确性，而且有助于提高计算速度。图5表示为柱面波的叠加阶数对声场计算结果的影响。

图4 声场计算结果与实验数据对比

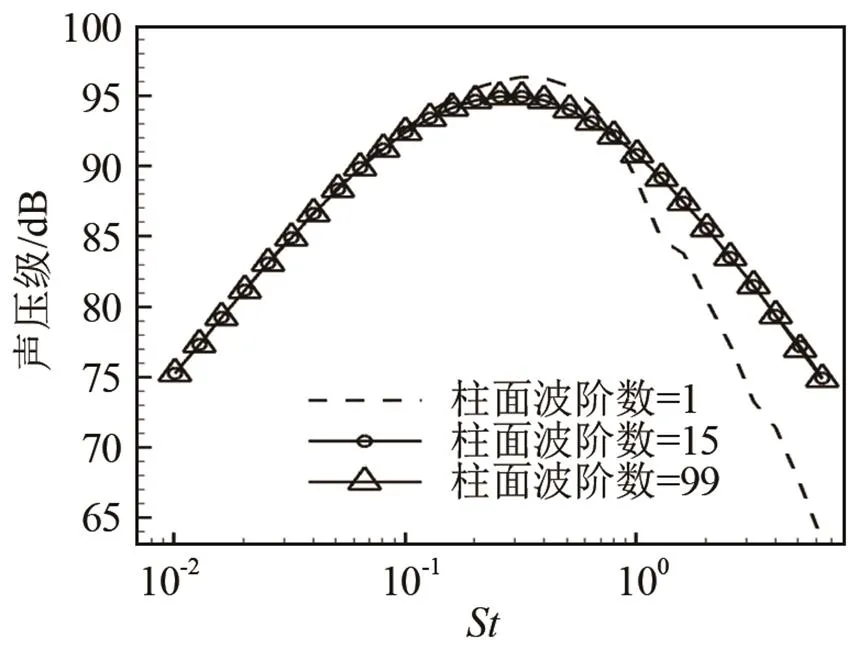
图5 不同柱面波阶数声场计算结果比较

由图5可知，在低频带内，较低的柱面波阶数，例如1阶柱面波，计算得到的声压级与99阶柱面波计算结果基本相等，而高频带内，低阶柱面波则出现了较大的偏差，该现象与模态理论相符合，即高频信息需要较高的模态进行描述。而当柱面波阶数取到15时，即和99阶柱面波的计算结果基本吻合，此时可认为既保证了足够的准确性，同时又能明显降低计算耗时，提高计算效率。

3 总结

本文介绍了基于TA模型的喷流噪声半经验预测方法的程序设计方法。

TA方法的理论模型不同于传统的声类比方法，在声源建模和声传播求解两方面都有较大的差异。本文首先对该理论模型进行分析讨论，然后通过商用软件ANSYS进行流场计算得到所需的平均流参数和湍流参数，进行声学网格划分和插值后，代入Fortran90代码中进行声场的计算，得到的声场计算结果与实验数据吻合较好。

本文同时提出一种简化的计算方法，在保证准确性的前提下，明显提高了声场计算的速度，这有利于在处理更复杂喷流场产生的声场时，提高计算效率，节省计算耗时。

[1] LIGHTHILL M J. On sound generated aerodynamically. i. general theory[J]. Proceedings of the Royal Society of London, 1952, 211(1107): 564-587.

[2] LIGHTHILL M J. On sound generated aerodynamically. ii. turbulence as a source of sound[J]. Proceedings of the Royal Society of London, 1954, 222(1148): 1-32.

[3] LILLEY G M, PLUMBLEE H E, STRAHLE W C, et al. The generation and radiation of supersonic jet noise. volume iv. theory of turbulence generated jet noise, noise radiation from upstream sources, and combustion noise[J]. Cell Regeneration, 1972, 3(1): 1-11.

[4] BALSA T F, GLIEBE P R, KANTOLA R A, et al. High velocity jet noise source location and reduction. task 2. theoretical developments and basic experiments[M]. Cincinnati: Aircraft Exhaust Gases, 1978.

[5] KHAVARAN A. Role of anisotropy in turbulent mixing noise[J]. Aiaa Journal, 1999, 37(7): 832-841.

[6] TAM C K W, AURIAULT L. Jet mixing noise from fine-scale turbulence[J]. Aiaa Journal, 1999, 37(2): 145-153.

[7] KHAVARAN A, BRIDGES J, GEORGIADIS N. Prediction of turbulence-generated noise in unheated jets. part 1[M]. Cleveland: ASRC Corporation, 2005.

[8] O’REILLY C J, RICE H J. Investigation of a jet-noise-shielding methodology[J]. Aiaa Journal, 2015, 53(11): 1-11.

[9] DAVIES P O A L, FISHER M J, BARRATT M J. The characteristics of the Turbulence in the Mixing Region of a Round Jet[J]. Journal of Fluid Mechanics, 1963, 15(7): 37-367.

[10] TAM C K W, GOLEBIOWSKI M, SEINER J. On the two components of turbulent mixing noise from supersonic jets[C]//2013.

[11] VASILYEV O, LUND T, MOIN P. A general class of cummutative filters for les in complex geometries[J]. Journal of Computatonal Physics, 1998, 146(7): 82-104.

[12] TAM C K W, AURIAULT L. Mean flow refraction effects on sound radiated from localized sources in a jet[J]. Journal of Fluid Mechanics, 2002, 370(3): 149-174.

The design of computational codes of jet noise semi-empirical prediction model

ZHAO Wen1, MAO Dong-xing1, JIANG Zai-xiu1, QIU Sheng2, YING Ji-yong2

(1. Institute of Acoustics, Tongji University, Shanghai 200092, China; 2. AECC Commercial Aircraft Engine CO., LTD., Shanghai 200092, China)

This paper discusses the design process of computational codes of jet noise semi-empirical prediction method based on TA model. In this work, the flow field is simulated by ANSYS Software, such as ICEM and FLUENT. The sound pressure level is calculated by Fortran90 codes. The results of the computation codes agree well with the experiment data of Tam. We also refer to a simplification method to cut down the CPU time and satisfy the accuracy as well.

jet noise; semi-empirical; TA model

TU112

A

1000-3630(2018)-04-0350-04

10.16300/j.cnki.1000-3630.2018.04.010

2017-10-04;

2017-12-18

国家自然科学基金(51506189)、上海市商用航空发动机领域联合创新计划资助。

赵雯(1992－), 女, 山东即墨人, 博士研究生, 研究方向为气动噪声。

赵雯, E-mail: zhaowen_15@tongji.edu.cn