桥梁初始偏心下桥梁平衡转体称重实验原理研究
2018-10-11翟鹏程
翟鹏程 刘 涛 邹 汛
(1.山西交通控股集团有限公司晋城高速分公司 晋城 048000;2.武汉理工大学土木工程与建筑学院 武汉 430070; 3.武汉马房山理工工程结构检测有限公司 武汉 430070)
桥梁转体施工[1]始于20世纪40年代,是由于场地限制或者为了跨越铁道线路,而在其两侧通过支架搭建或利用现场地形进行现场浇筑,再通过结构的转动将梁体合龙的施工方法。我国已建的转体施工桥梁约有100余座[2]。转体施工中为保证桥梁转体的安全平稳,则需要进行称重实验来确定桥梁的偏心情况,并加以配重保证转体桥球铰中心承重,同时确定球铰的摩擦系数及启动牵引力。
关于称重实验的原理现已有很多研究成果[3-5]。颜华惠等[6]对现行称重实验测量球铰静摩阻力进行了改进,但未考虑初始偏心的影响。郭宁等[7]在计算启动牵引力的时候,考虑了滑道对转动的影响,但未考虑初始偏心距对转体系统的影响。本文基于现有称重实验原理,考虑初始偏心距的影响,并用实际工程进行计算分析,验证考虑初始偏心距计算方法的优越性。
1 称重实验原理
桥梁转体要顺利、安全、平稳,必须保证梁体在转动过程中始终处于平稳状态,并且牵引系统能提供充足、稳定的牵引力。
通过转体重心计算偏心距,由于各参数无法全部精确控制获取,会存在实际偏心与理论计算不一致的情况,因此,需要在转体前进行称重试验,以了解结构的实际偏心状态,通过称重试验测试转动体的不平衡力矩及静摩阻系数,从而制定相应的配重实验方案,并根据实际支承情况计算启动牵引力,确保牵引系统的动力安全系数满足要求。
1.1 摩阻力矩大于转动不平衡力矩
1) 考虑初始偏心距对结果的影响。在转动梁体左侧用千斤顶进行顶升,当顶升力矩等于摩阻力矩及不平衡力矩之和,再加大顶升力时,梁体由原先的静摩阻力变为动摩阻力,此时,梁体球铰产生微小转动,如图1所示,图中假设偏心在左侧。

图1 左侧顶升
此时平衡方程为
P1(L1-e)-Ge=MZ
(1)
式中:P1为沿纵轴线左侧千斤顶顶推过程中使球铰产生微小转动瞬间的顶力;L1为顶推力至球铰中心处力臂长度;e为桥梁重心偏心距;G为桥梁重量;MZ为摩阻力矩。
在转动梁体右侧用千斤顶进行顶升,当顶升力矩及不平衡力矩之和等于摩阻力矩,再加大顶升力时,梁体由原先的静摩阻力变为动摩阻力,此时,梁体球铰产生微小转动,受力示意见图2。

图2 右侧顶升
此时平衡方程为
P2(L2+e)+Ge=MZ
(2)
式中:P2为沿纵轴线右侧千斤顶顶推过程中使球铰产生微小转动瞬间的顶力;L2为顶推力至球铰中心处力臂长度。
结合式(1)与式(2),即可得到
(3)
(4)
Mg=Ge
(5)
(6)
式中:Mg为转动不平衡力矩;μ为静摩擦系数;R为球铰球面半径。
根据现行规范,可得到转体启动牵引力
(7)
式中:D为启动牵引力偶臂。
2) 不考虑初始偏心距的影响。若不考虑初始偏心距,得e与MZ为
(8)
(9)
1.2 摩阻力矩小于转动不平衡力矩
1) 考虑初始偏心距对结果的影响。当MZ 当撑脚与滑道接触时,此时只能在撑脚落地一侧施加顶推力,当顶升力矩等于摩阻力矩及不平衡力矩之和,再加大顶升力时,梁体由原先的静摩阻力变为动摩阻力,此时,梁体球铰产生微小转动,如图3所示,图中仍假设偏心在左。 图3 左侧顶升 此时平衡方程为 P1(L1-e)-Ge=MZ (10) 继续试验,此时左侧千斤顶开始卸载回落,当顶升力矩与摩阻力矩之和等于不平衡力矩,再减小顶升力时,梁体由原先的静摩阻力变为动摩阻力,此时,梁体球铰产生微小转动,如图4所示。 图4 右侧顶升 此时平衡方程为 Ge-P(L1-e)=MZ (11) 式中:P为千斤顶回落过程中球铰产生瞬时转动的顶力。 结合(10)与(11),即可得到 (12) (13) 其他参数计算,均同于式(5)~(7)。 2) 不考虑初始偏心距的影响。若不考虑初始偏心距,则得出结果e与MZ为 (14) (15) 本桥为汉十高铁65 m+100 m+65 m悬臂施工预应力连续梁桥,其跨越下方铁路交通系统,转体系统桥梁布置见图5,转体部分主要参数见表1。 图5 主桥布置图(单位:cm) 表1 转体系统主要参数 称重试验测试仪器布置见图6、图7。 图6 称重试验仪器布置立面图(单位:cm) 图7 称重试验球铰处仪器布置平面图(单位:cm) 在桥梁转动体两侧对称于桥梁中心线布置4台4 000 kN千斤顶,用以在称重试验时对转动体进行顶放,测试试验过程中临时支点的反力值。 如图8、图9所示,在两侧撑脚处位置布置4个竖向百分表,记录每级加载时相应的竖向位移。在相邻位置布置4个水平向百分表记录每级加载时相应的水平位移,用以综合判断球铰转动的临界状态,合理确定临界力值。 图8 百分表横向布置大样图(单位:cm) 图9 百分表竖向布置大样图(单位:cm) 取319号墩测试结果,如表2 、表3所示。 表2 中跨侧加载位移数据 注:表中竖向位移值正号为上升,负号为下降;横向位移以十堰方向为正,以武汉方向为负。 表3 边跨侧加载位移数据 注:表中竖向位移值正号为上升,负号为下降;横向位移以十堰方向为正,以武汉方向为负。 根据表2绘制中跨力-位移曲线,见图10。 图10 中跨侧顶升力-位移变化图 由图10可知,中跨侧突变值P1=1 241.3 kN。 根据表3绘制边跨力-位移曲线见图11。 图11 边跨侧顶升力-位移变化图 由图11可知,边跨侧突变值P2=2 342.6 kN。 由于顶升之前,转体系统没有滑落,则可知摩阻力矩大于不平衡力矩,则通过考虑初始偏心距可计算出结果,并汇总于表4。 表4 考虑初始偏心距结果 若运用不考虑初始偏心距的公式计算,则结果汇总于表5。 表5 不考虑初始偏心距结果 由于实际启动牵引力为400 kN,考虑初始偏心其结果误差为13.1%,而规范算法为71.7%,因此,考虑初始偏心距算法在精度上有明显提升。 1) 静摩擦系数计算精度提升,从而提升了启动牵引力的精确度,确保了桥梁转体启动的安全性。 2) 现场由于启动操作等误差存在,有可能导致实验数据精确度不足,因而在算法上需要更加精确。考虑初始偏心距更加符合工程情况。

2 工程实例分析
2.1 工程概况


2.2 测点布置


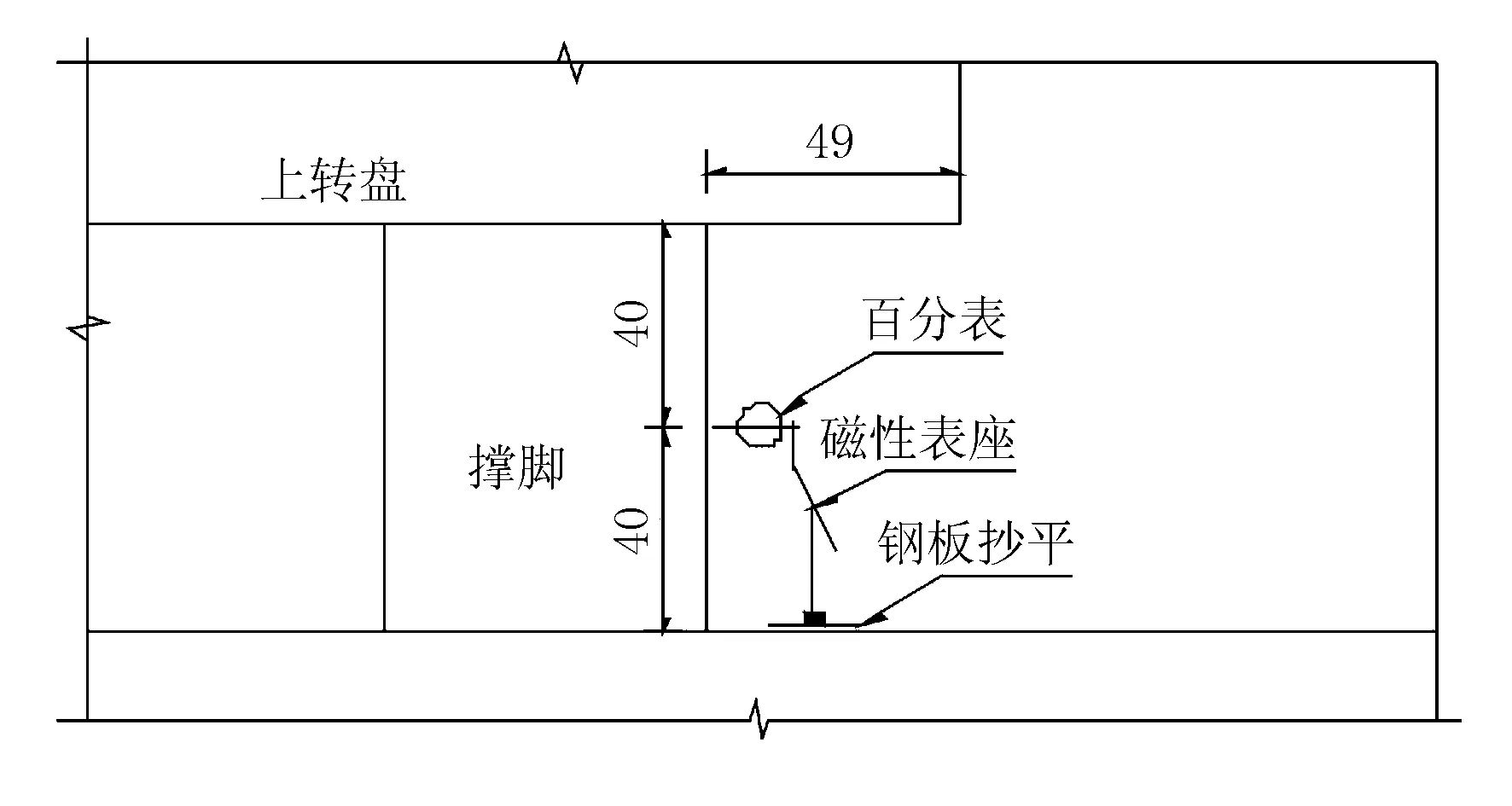
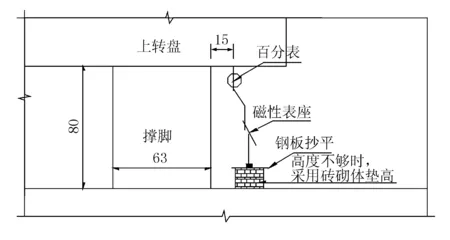
2.3 测试结果及分析






3 结论
