球鼻艏船舶鼻艏正撞弹性变形系数研究

贾恩实

(中铁大桥勘测设计院集团有限公司 武汉 430056)

1 铁路桥涵设计规范船撞力计算公式

船撞桥是一个复杂的动力过程，船撞桥的研究及相关结构设计宜采用动力学理论和方法。然而，因桥梁结构防船撞设计的动力设计方法尚不完备，目前世界各国桥梁设计规范对于桥梁结构防船撞设计仍采用“静力法”。桥梁结构防船撞设计“静力法”是利用功能原理将船撞动力效应等效成一个静力值来进行结构设计的方法。该等效静力值可通过多种方法获得，如经验公式法[1]、数值模拟法[2-3]及有限元动力仿真法[4]等。

我国现行铁路桥涵设计规范[5]对于桥梁结构的防船撞设计沿用“静力法”，并采用经验公式(1)对该等效静力进行估算。

(1)

式中:F为撞击力，kN；γ为动能折减系数，s/m1/2，当船只或排筏斜向撞击(船只或排筏驶近方向与撞击点处墩台面法线方向不一致)墩台时可采用0.2，正向撞击(船只或排筏驶近方向与撞击点墩台面处法线方向一致)时可用0.3，考虑设置吸能防护措施时，应适当折减，折减值应通过试验研究；v为船只或排筏撞击墩台时的速度，m/s，此项速度对于船只采用航运部门提供的数据，对于排筏可采用筏运期的水流速度；α为船只或排筏驶近方向与墩台撞击点处切线所成的夹角，根据具体情况确定，如有困难，可采用α=20°；W为船只重或排筏重，kN；C1，C2为船只或排筏的弹性变形系数和墩台圬工的弹件变形系数，m/kN，缺乏资料时可假定C1+C2=0.000 5 m/kN。

2 船艏变形弹性系数含义

我国铁路桥涵设计规范船撞力计算经验公式由机械能守恒原理推导而来，其假定在船撞过程中，除船体绕撞击点的旋转动能和沿碰撞面的滑移动能外，其余动能均转化为船舶和桥墩的变形能；假定船撞过程中船舶、桥墩的“碰撞力-变形”关系均为一次线性关系，如图1所示。根据上述假定，当船舶以α夹角撞击撞桥墩，依据功能原理可列出式(2)

(2)

式中：ρ为考虑船体旋转的动能系数；m为船舶撞击质量；v为初撞速度；α为船速方向与墩台切向所成的夹角；F为最大碰撞力；l1为船舶变形；l2为桥墩变形。等号左侧多项式为船舶参与的碰撞动能，等号右侧多项式为按碰撞力与碰撞变形成线性关系推导的静力功。

图1 计算图示

定义船舶弹性变形系数C1=l1/F、桥墩弹性变形系数C2=l2/F。

将C1，C2变形后代入式(2)可得

(3)

将式(3)中m用W/g表示，得

(4)

正撞桥墩时，船舶不产生旋转亦不产生滑移，故ρ=1，α=90°，式(1)简化为

(5)

由以上分析可知，船艏弹性变形系数C1本质是船舶抗撞柔度系数，是船艏的结构固有属性，与船艏结构的构造及材料相关。不同的船舶有不同的C1值，同一艘船舶在不同的碰撞工况下C1值也不相同。

我国学者梁文娟等[6-7]曾采用“非线性弹簧”假设对多艘船舶的船艏弹性系数进行过计算，结果见表1。表1中各船的船艏弹性变形系数各不相同，且与规范建议的取值C1+C2=0.000 5 m/kN相差甚远。可见，C1值的取用是规范公式的关键，为使经验公式计算合理，需取用合理的C1值。

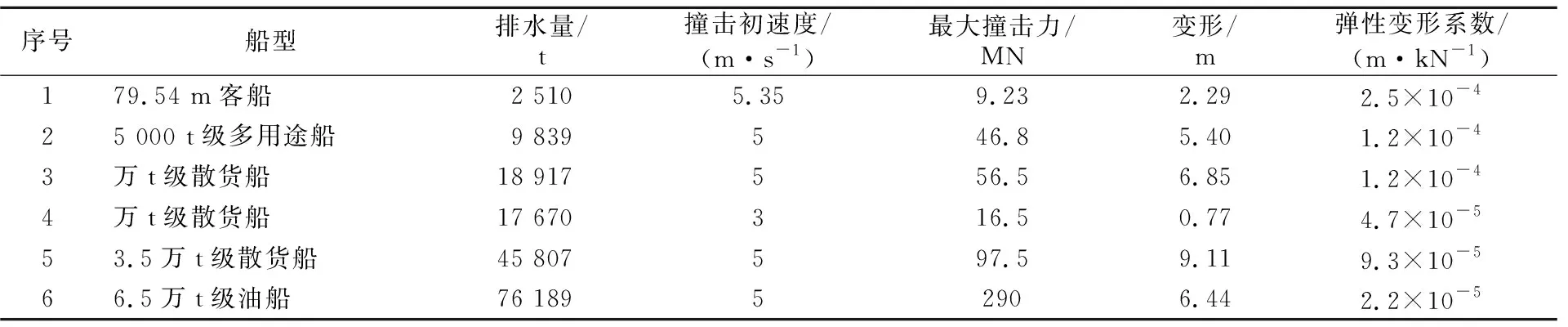
表1 部分船型船艏弹性变形系数表

3 船球鼻艏正撞弹性变形系数研究

采用有限元软件建立3 000 t级散货船球鼻艏正撞刚性墙的三维仿真模型，通过计算获得碰撞过程中船艏“碰撞力-撞深”“弹性变形系数-撞深”曲线，并对结果进行分析研究，期望获得关于鼻艏正撞弹性变形系数的一些有益结论(文献[8]将正撞过程中船艏的变形称为 “撞深”，将“碰撞力-船艏变形”曲线称为“碰撞力-撞深” 曲线，本文沿用该说法)。

仿真模型所用船舶总长96.6 m、型宽15 m、型深6.7 m，设计吃水5.2 m、满载排水量5 300 t。材料模型考虑了应变率及应力强化效应，船艏模型见图2。计算结果见表2、图3～图8。结果给出了该船在同重不同速、同速不同重、同能不同速重等3类情况下的船鼻艏“碰撞力-撞深”(F-L1)曲线、“弹性变形系数-撞深”(C1-L1)曲线及相关数据结果。计算结果中W为撞击重量；v为初撞速度；E0为初撞动能；Fmax为撞击力峰值；L1为Fmax对应的船鼻艏撞深；E为Fmax对应的船舶动能值；C1为船鼻艏弹性变形系数；E余为在撞击力峰值后仍参与转化的船舶动能余量百分比；a为功能等效调整系数，a=E/(0.5FmaxL1)。需说明的是，模型中桥墩被简化为刚性墙具有无穷刚度，即C2=0。

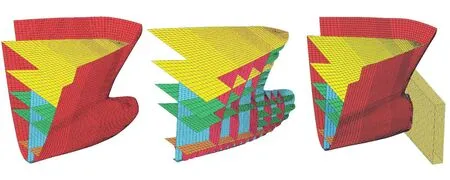
图2 载重量3 000 t散货船船艏内外侧模型图

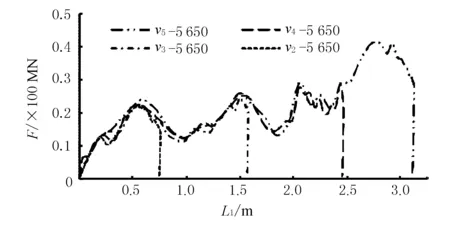
图3 同重F-L1曲线

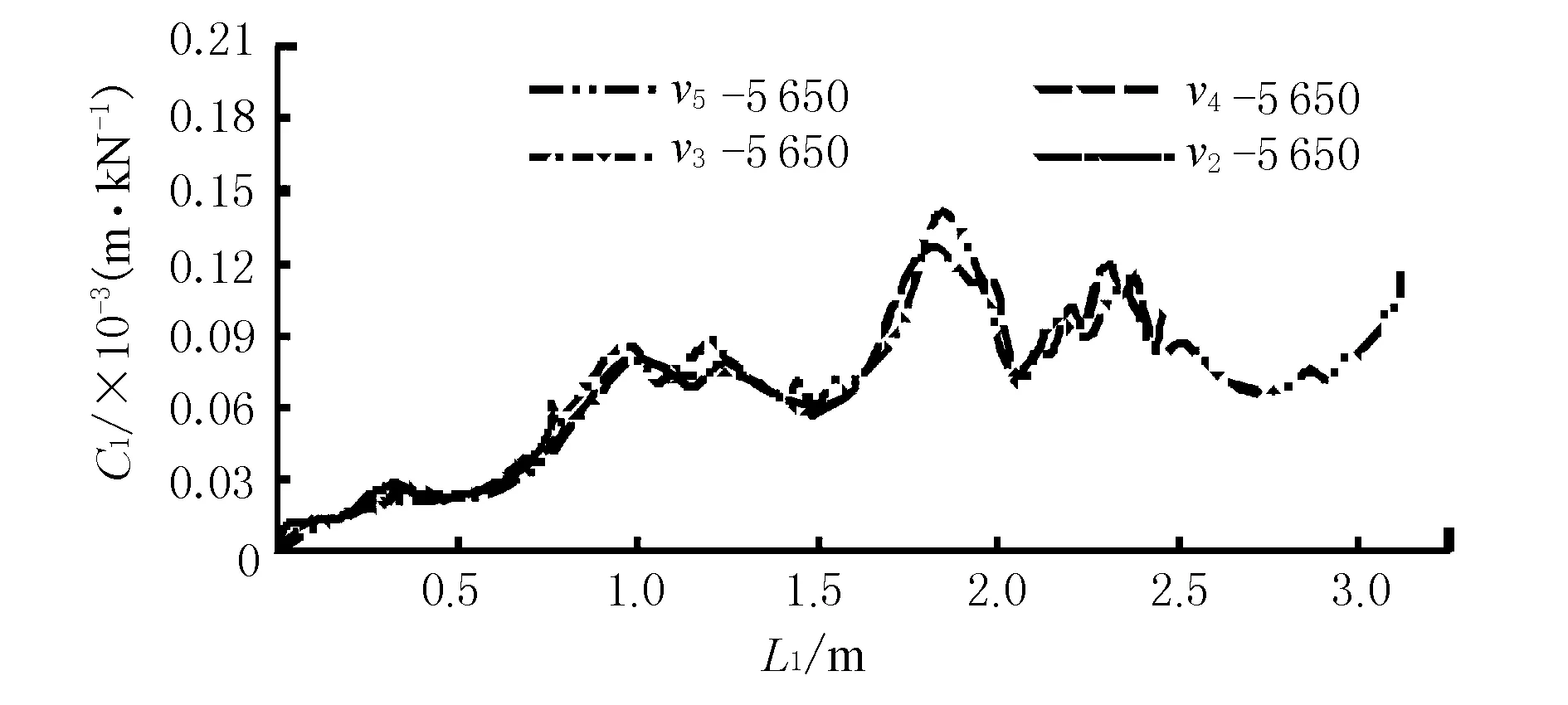
图4 同重C1-L1曲线

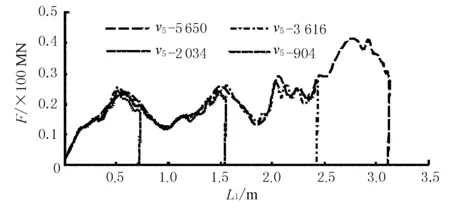
图5 同速F-L1曲线

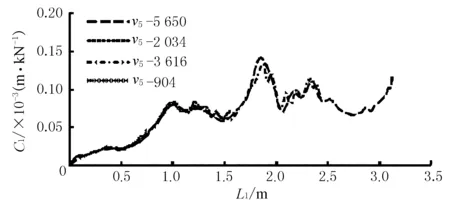
图6 同速C1-L1曲线

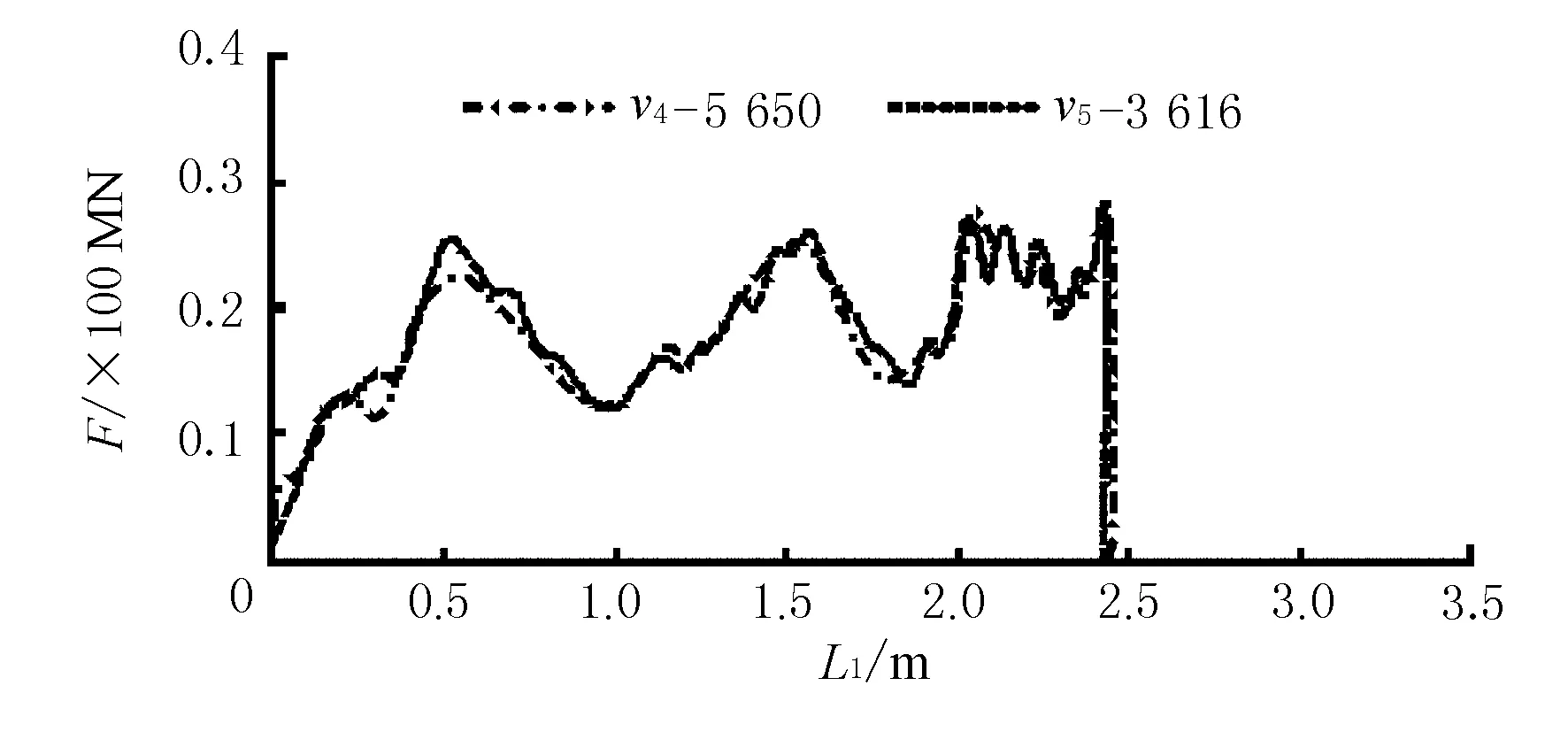
图7 同能F-L1曲线

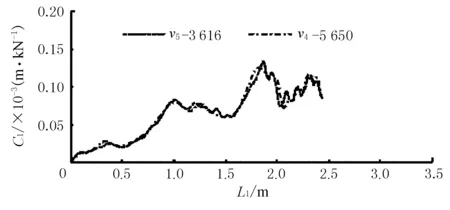
图8 同能C1-L1曲线

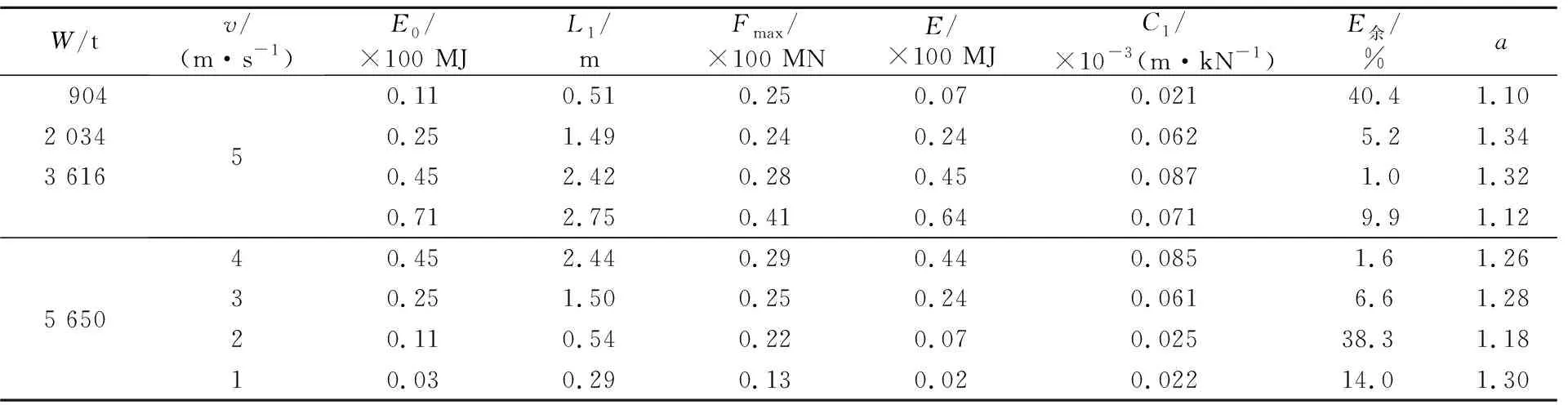
W/tv/(m·s-1)E0/×100 MJL1/mFmax/×100 MNE/×100 MJC1/×10-3(m·kN-1)E余/%a 9042 0343 61650.110.510.250.070.02140.41.100.251.490.240.240.0625.21.340.452.420.280.450.0871.01.320.712.750.410.640.0719.91.12 5 65040.452.440.290.440.0851.61.2630.251.500.250.240.0616.61.2820.110.540.220.070.02538.31.1810.030.290.130.020.02214.01.30

结果表明，对于同一艘船舶，撞深是由船舶所吸收的动能决定的。正撞时绝大部分初撞动能均由船艏吸收(不考虑防撞设施)，故初撞动能决定撞深，同一初撞动能(可由不同质量、速度组成)具有基本一致的撞深。

船鼻艏弹性变形系数并非定值，随船艏撞深变化而变化并一一对应；整体而言船鼻艏弹性变形系数有随撞深增大而增大的趋势。弹性变形系数亦由船艏所吸收动能决定；正撞时初撞动能决定船鼻艏弹性变形系数，同初撞动能作用下船艏表现出基本一致的弹性变形系数。

简言之，正撞船鼻艏弹性变形系数是一个随船舶初撞动能变化而变化的动态值。

另外还注意到在表2中E余基本都大于0，即最大碰撞力与最大碰撞动能不相对应；撞击力与撞深不成一次线性关系，等效静力功不宜简单按线性关系计算，需在此基础上考虑静力功调整系数a，a介于1.1～1.3之间。

4 结论

本文通过对典型载重量3 000 t球鼻艏散货船鼻艏正撞弹性变形系数的研究可知：①鼻艏正撞弹性变形系数是一个随船舶初撞动能变化而变化的动态值；②最大碰撞力与最大碰撞动能不相对应；③撞击力与撞深非一次线性关系，等效静力功不宜简单按线性关系计算。

故根据以上结论，当采用我国铁路桥涵船撞力计算公式进行该船船艏正撞力估算时，为获得比较正确的结果，可按下述方法进行。①将正撞船艏弹性变形系数按初撞动能分级取用；②静力功计入调整系数；③如调整系数取1.2，则正撞力可按式(6)计算。

(6)

式中:C1为按E0分级取用的弹性变形系数，E0为初撞动能。

(7)

表3为载重量3 000 t球鼻艏船鼻艏正撞弹性变形分级表，分级过程见图9：碰撞仿真获得“碰撞力-能量”曲线(f-E)；标出F曲线中碰撞力峰值(f)对应的能量级并定为分级点；利用“碰撞力-撞深”曲线求得分级点弹性变形系数。

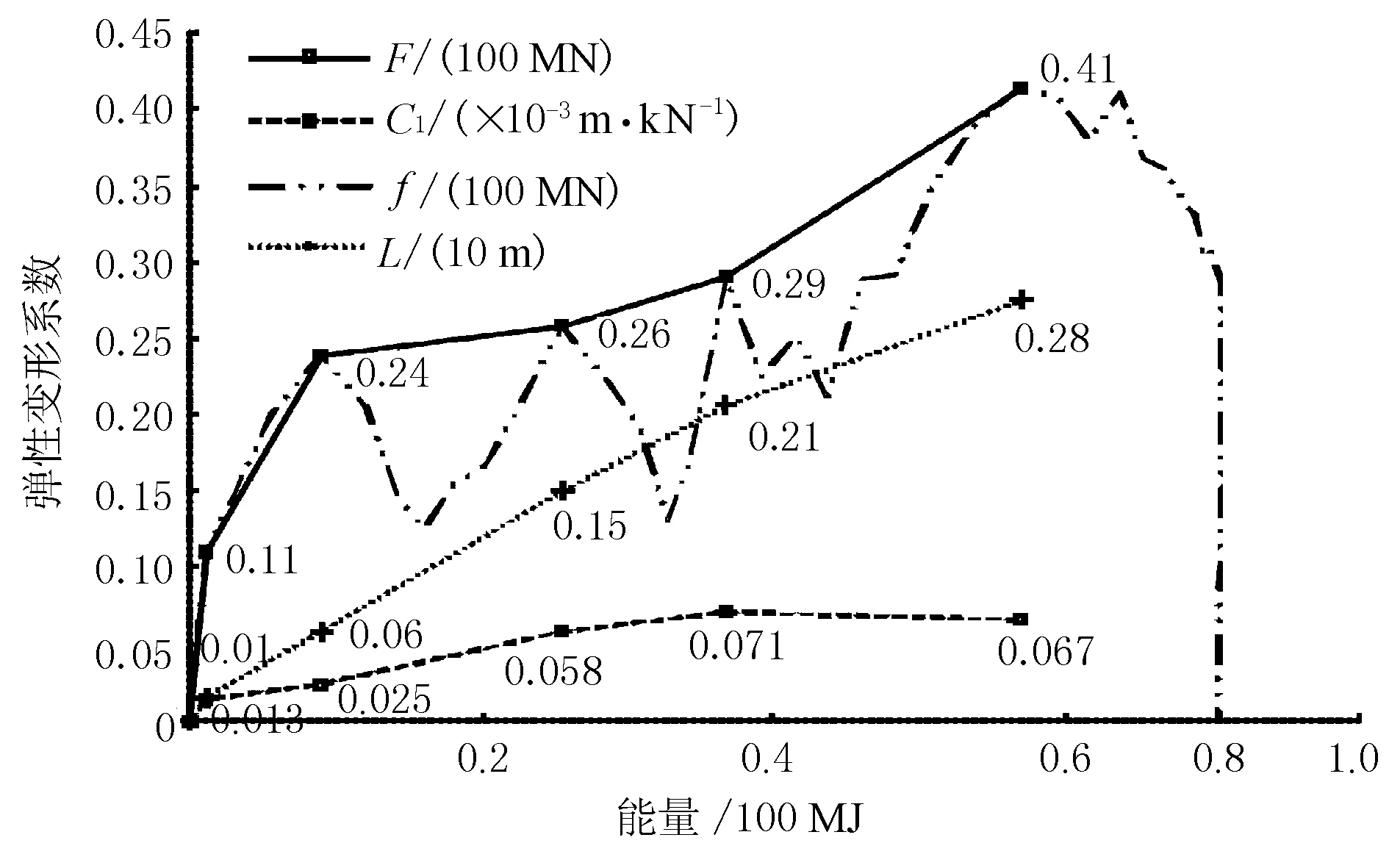
图9 载重量3 000 t球鼻艏散货船船鼻艏弹性变形系数分级图

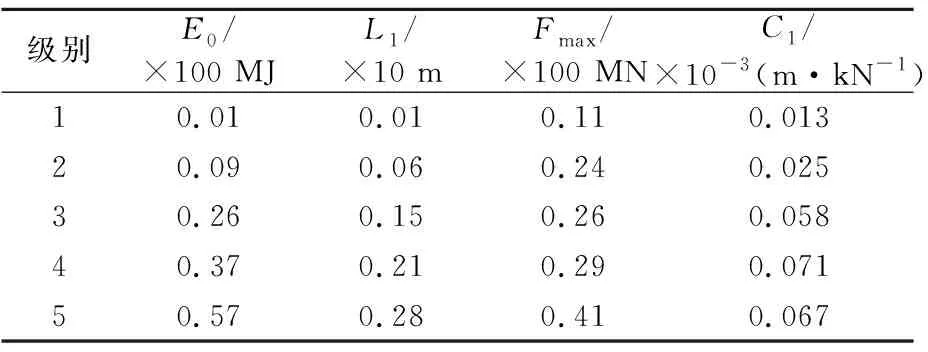
级别E0/×100 MJL1/×10 mFmax/×100 MNC1/×10-3(m·kN-1)10.010.010.110.01320.090.060.240.02530.260.150.260.05840.370.210.290.07150.570.280.410.067

注：其他能量级正撞弹性变形系数线性插值使用。

5 建议

虽本文研究的是船鼻艏正撞时弹性变形系数的分布规律，但若推广到整艏正撞，前述3条结论都基本成立。同理，若将该研究推广至其他各类型各吨级船舶的船艏正撞，前述结论亦可成立。本文的研究思路与方法，可为其他各类型各吨级船舶的船只弹性变形系数研究提供参考。最后，建议当采用铁路桥涵设计规范船撞力计算公式计算船撞力时，为获得正确的计算结果，船只弹性变形系数应按船撞初动能分级取用，同时在公式中计入静力功调整系数。