新建隧道下穿既有地铁爆破施工数值模拟

2018-10-11张前进崔帅帅于雅琳张乐文

交通科学与工程 2018年3期

张前进, 武科, 崔帅帅, 于雅琳, 张乐文

(1.山东大学土建与水利学院，山东济南 250061; 2.山东大学海洋研究院，山东青岛 266237)

随着社会的不断发展，地下工程已成为城市建设的重要部分。隧道能够压缩城市空间，方便人们的出行，在交通运输中起着重要的作用，被大量运用于城市建设中。但是，地下空间有限，有时会遇到隧道下穿情况，下穿隧道的建设势必会给既有隧道带来影响，产生地面沉降、既有隧道变形及土层变形等危害。由于用矿山法开挖隧道的爆破会产生爆轰波，严重影响了既有结构的稳定性[1-7]，因此，在地铁爆破过程中，需要研究工程爆破对既有结构的影响，预测结构受力变形。

关于工程爆破振动的研究有很多。周俊汝[8]等人基于粘性岩体爆破振动频谱表达式,并结合LS-DYNA有限元软件,对球状药包爆破振动主频和平均频率的衰减机制及其规律进行了分析。张震[9]等人采用现场监测和动力有限元数值模拟相结合的研究方法,对超浅埋地铁站通道爆破开挖邻近埋地混凝土管道的动力响应进行了研究。邓锷[10]等人运用数值模拟方法,分别研究了不同顶板厚度下隧道爆破施工引起的围岩振速分布特征及其对围岩的损伤情况,并对围岩稳定性进行了分析。Jun[11]等人为了研究隧道爆破引起的冲击波传播衰减，建立了具有爆破效果的三维模型。

有关学者研究振动载荷的影响集中于地表的振动速度和冲击波的衰减规律,而研究下穿既有隧道时爆破施工对既有结构的影响及选择合理的施工方法较少[12-14]。作者拟在数值模拟软件Flac3D的基础上，结合具体工程实例，对爆破载荷作用下新建隧道与既有隧道的应力和变形情况进行分析，研究地层和拱顶沉降，以期对相关施工进行指导。

1 工程概况

既有地铁隧道采用土压平衡盾构建造。该盾构隧道外径为6.0 m，内径为5.4 m。隧道管片由六块拼装而成，管片宽度为1.5 m。新建地铁隧道部分区间采用矿山法建造，新、旧隧道夹角约为85°。新建地铁隧道下穿既有隧道，新建隧道埋深18.2 m，新建隧道与既有隧道右线与左线最小净距分别为7.5和1.8 m。为了确保下穿期间既有隧道的安全，穿越过程中对既有隧道变形进行了实时监测。沿既有隧道与新建隧道的交界处布置了断面检测，断面的间隔5～6 m。此外，对隧道附近同一埋深带点的地表沉降进行了检测，断面距隧道边缘2～3 m。隧道的地层和监测点布置分别如图1，2所示。

图1 地层Fig. 1 Stratigraphy

图2 监测点布置(单位：m)Fig. 2 The layout of the monitoring point(unit:m)

2 数值计算模型与分析方法

2.1 数值近似模型

采用 FLAC 3D有限差分软件，对下穿既有隧道的爆破过程进行数值模拟，研究新建隧道爆破对既有隧道的动力响应。该模型为马蹄形隧道，由既有隧道和土体组成。模型中新建隧道横向取54 m，竖向取50 m，轴向取70 m。模型土体采用Mohr-Coulomb模型，新建隧道衬砌与既有隧道按照弹性模型进行计算。隧道模型如图3所示。

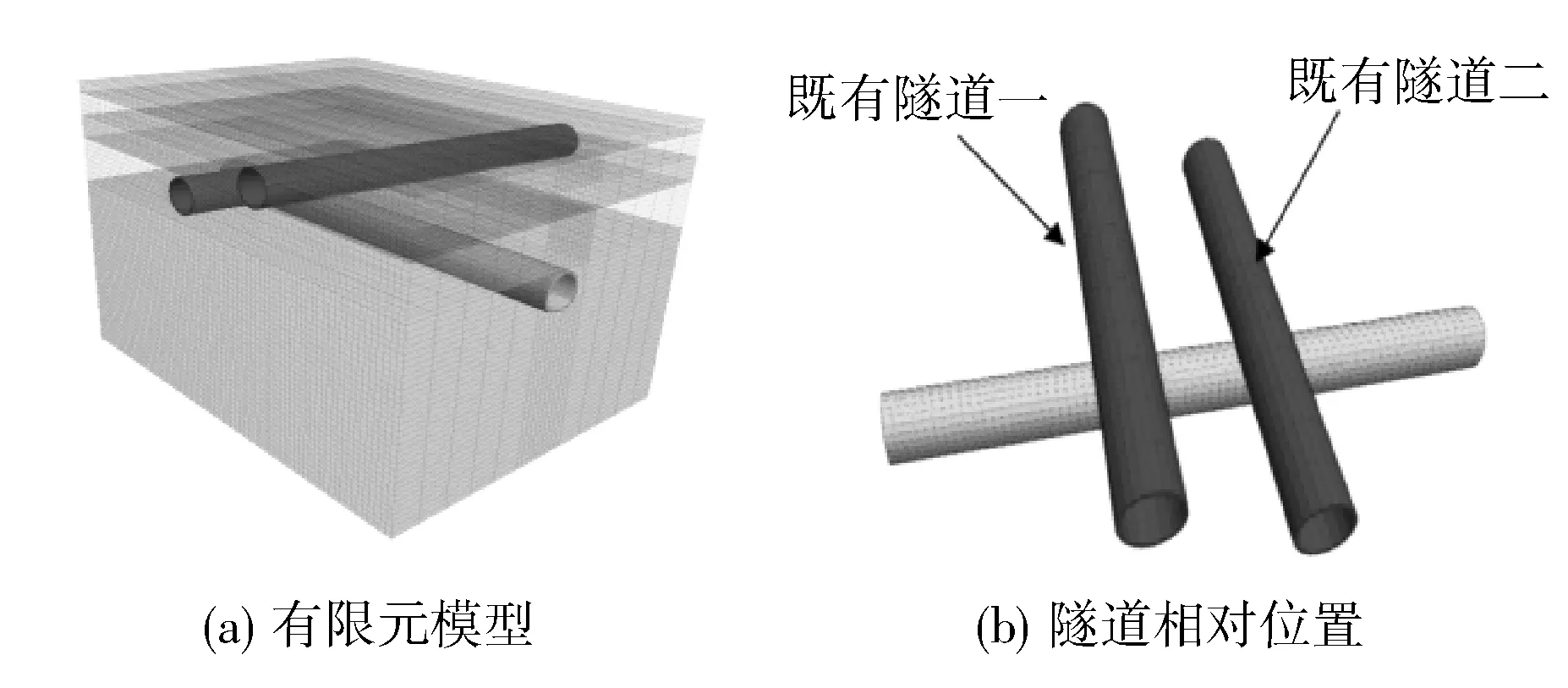
图3 隧道模型Fig. 3 Tunnel model

2.2 岩土介质力学参数

根据现场地质勘查情况，隧址区土体由素填土、细粉砂、砾质粘性土、全风化花岗岩及强风化花岗岩等组成。具体土层和支护参数见表1。

2.3 数值计算分析方法

2.3.1 数值计算步骤

工程爆破数值模拟计算分为静力计算和动力计算2部分。在静力模拟的基础上才能进行动力模拟。Flac3D数值模拟步骤为：① 建立模型，进行网格划分并确定动力参数；② 定义静力条件下的初始边界条件；③ 进行重力平衡计算，然后进行隧道静力开挖模拟，得到开挖后的结果；④ 选择动力模式，设置动力边界条件和阻尼条件；⑤ 施加动力载荷，进行动力计算，得到模拟结果。

2.3.2 动载荷施加

在动力计算中，边界条件包括粘性边界条件和自由边界条件。动力计算模拟开挖使用粘性边界。采用粘滞边界条件就是在模拟行的前、后、左、右边界以及下边界设置粘滞边界条件，上边界为自由边界。力学阻尼包括瑞利阻尼、局部阻尼和滞后阻尼。现采用瑞利阻尼，其临界阻尼比为5%，中心频率取100 Hz。

为了准确地模拟隧道施工过程中的冲击载荷，采用载荷作用时间和爆破冲击载荷经验公式来施加动力载荷[12]。

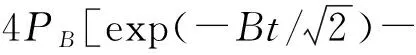
(1)

(2)

(3)

式中：PD(t)为爆破冲击载荷；B为载荷常量；t为作用时间；PB为实测爆轰速度D和密度ρ0时的炸药爆轰压力；Sge为炸药密度；ve为爆轰速度；μ为泊松比；m为装药质量[14]。

施加动载荷方式为：将动载荷施加在垂直隧道壁新建隧道的周围。在模拟静载荷下施工完成后，施加动载荷，位置为一次爆破循环作用的管壁，动载荷总体作用时间为0.2 s，动载荷施加的方向为垂直于管壁向外，如图4所示。通过实际测量，得到的参数有：实测爆轰速度为3.5 km/s；密度为1 g/cm3；泊松比为0.23；装药质量为28 kg。

图4 爆破时程载荷Fig. 4 Blasting time versus the load

3 结果分析

3.1 新建地铁隧道稳定性分析

3.1.1 应变分析

爆破载荷的作用下，新建隧道和土体的应变会发生改变。隧道的位移云图如图5所示。

从图5中可以看出，静载下竖向位移最大为2.57 cm，施加爆破载荷后最大竖向位移为2.83 cm，竖向位移增加了0.26 cm。竖向位移沉降最大处在拱顶部分，最大隆起出现在拱底。静载下水平位移为0.77 cm，施加爆破载荷后水平位移的最大值为1 cm，增加了2.3 mm。

经过施加动载荷，竖向沉降增加了约10%，水平位移增加了约30%。这是由于竖向位移受重力作用影响较大，动载荷影响沉降不是主要作用因素，因此竖向位移增加得不多。水平位移受重力作用的影响较小，但施加动载荷后其所受影响较大。在爆破开挖的隧道中，不仅要考虑竖向位移，更要加强水平方向的支护措施来减小爆破振动所产生的影响。

图5 位移云图Fig. 5 Displacement cloud

在模拟过程中，对断面MC-C爆破区间内5个点的竖向位移进行了检测，检测点位置和竖向位移的变化分别如图6，7所示。

图6 检测点位置Fig. 6 Test point location

图7 竖向位移与时间的关系Fig. 7 Relationship between vertical displacement and time

从图7中可以看出，隧道的拱顶与拱腰处的监测点位移趋势相同。经过施加爆破载荷后，位移先减小后增加，最后趋于稳定。检测点1的位移由-2.5 cm减小到-1.3 cm。随着爆破载荷逐渐减小，位移又逐渐增加，最后，稳定在-2.8 cm附近。拱底的位移在动载荷的作用下由隆起变成沉降，然后，随着载荷的不断减小，又变为隆起。检测点5的位移由-0.8 cm变为0 cm，然后，又逐渐增加，最后，稳定在-1.1 cm附近。

监测点的变化趋势与动载荷的变化趋势有关。在0.02 s处位移出现明显转折，0.06 s后动载荷消失，位移趋于稳定。经动载荷作用后，隧道上部分为沉降且位移增加，拱底位移略有减小。在爆破施工过程中，由于爆破作用，隧道的位移会超过最终的稳定值，并且中间波动量较大，因此，对隧道的防护要考虑到爆破过程中位移的变化，对于隧道稳定性的防护要留有一定的安全空间，防止因爆破波动过大而造成的破坏。

3.1.2 应力分析

为了分析衬砌的受力情况，对隧道衬砌的最大正应力与最小正应力进行了分析，应力云图如图8所示。从图8中可以看出，在施加动载后，最小正应力由3.2 MPa变为3.7 MPa，增加了16%。在爆破的作用下，最大正应力由1.7 MPa增加到2 MPa。动载荷对最小正应力和最大正应力应力的影响都比较大，施加动载荷后应力整体增加了约16%，因此，要加强材料和结构的强度来降低爆破振动的影响。

图8 应力云图Fig. 8 Stress cloud

新建隧道最小主应力受压，并分布在拱腰附近，拱顶受力较小。在动载荷的作用下，最小主应力在拱腰部分的压应力逐渐增加，而既有隧道的压应力有所减小。新建隧道的最大正应力产生在拱顶位置，拱腰受压，既有隧道在拱顶和拱底受压较大。在动载荷的作用下，新建隧道拱腰的压应力作用区域增加，而压应力的最大值减小，拉应力增加了18%。因此，动载荷使新建隧道和既有隧道的应力都增加，但是爆破作用对新建隧道的影响要大于既有隧道的。处于隧道爆破位置的主应力的变化最为明显，其原因是振动作用距离爆破位置越远，振动作用越小。要重点加强爆破位置的防护，防止局部结构因超过极限条件而遭受破坏。

3.2 既有地铁隧道稳定性分析

3.2.1 既有结构地层沉降

对MC-A和MC-B点的地层沉降进行了检测分析，地层沉降曲线如图9所示。

从图9中可以看出，MC-A断面最大沉降的实测值为9.5 mm，而最大沉降的模拟值为8.1 mm。MC-B断面最大沉降的实测值为7.8 mm，而最大沉降的模拟值为6.2 mm。模拟值比实测值小1 mm左右。实际测量值与模拟值曲线趋势相同，距离隧道中心处的位移最大。随着与新建隧道距离的增加，地层沉降不断减小。因此，要在新建隧道附近区域进行重点防护。另外，既有隧道二附近断面MC-A的沉降大于既有隧道一附近的断面MC-B的沉降。表明：距爆破点较远的既有隧道一受到爆破的影响比距爆破点较近的既有隧道二受到爆破的影响要小。用Flac 3D建立的数值计算模型偏差较小，其结果较为准确。

3.2.2 既有隧道拱顶沉降

根据图2监测点的布置，对隧道拱顶和地层的沉降进行监测。各点的沉降如图10所示。

从图10中可以看出，既有隧道一在静载下拱顶的最大沉降为3.5 mm。施加动载后，拱顶的最大沉降为3.9 mm，增加了0.4 mm，约为11.4%。既有隧道二在静载下拱顶的最大沉降为3.47 mm。发生爆破后，拱顶的最大沉降为5 mm，增加了1.53 mm，约为44%。动载荷对既有隧道二的影响大于对既有隧道一的，其原因是既有隧道二距新建隧道较近，受爆破振动的影响较大。因此，在爆破位置周围要加强支护，远离新建隧道部分的支护可在允许范围内适当减少。

随着到既有隧道拱顶距离的增加，地层沉降也会增加。在动载作用下，既有隧道一拱顶最大沉降由3.5 mm增加到4.4 mm，既有隧道二拱顶最大沉降由5 mm增加到6.8 mm。其原因是缺少隧道管片的支护，使得地层沉降增加。在既有隧道拱顶处，由于衬砌支撑作用，其沉降较隧道两侧的小。因此，要加强距爆破位置近部分的支护，防止因结构振动造成的破坏，还要加强既有隧道周围土体的强度，以减少地层沉降。

3.2.3 台阶法模拟爆破

将全断面开挖爆破改为台阶法开挖爆破，会使爆破对隧道的影响降低。对既有隧道一断面MC-6处的振动速度进行了检测，监测点的位置与MC-C的布置相同。分别采用全断面爆破和台阶法爆破的方式进行隧道开挖，监测点的振动速度如图11所示。

图11 监测点振动速度Fig. 11 The vibration speed at the monitoring point

从图11中可以看出，全断面爆破开挖的振动速度最大值为5.2 cm/s，台阶法爆破开挖的振动速度的最大值为3.7 cm/s，台阶法爆破比全断面爆破的最大振动速度减少了1.5 cm/s。随着时间的增加，振动呈现先增长后减小的状况，在7 ms左右出现峰值，然后不断波动，最后趋向于0 cm/s。台阶法爆破的曲线整体小于全断面爆破的，台阶法爆破产生的影响比全断面爆破产生的影响降低了28.8%，并且台阶法爆破产生的振动较早地消失，施工更安全。

从图11中还可以看出，较其他监测点的振幅，位于既有隧道拱底监测点6的振幅最大，监测点1的振幅最小。在台阶法爆破第一次速度峰值中，监测点6的速度为3.7 cm/s，位于拱顶的监测点1的振动速度为1.05 cm/s，位于隧道中部其他监测点的振动速度处于这2个速度之间。表明：振动的幅度与距爆破点的位置有关。距爆破点越近，受到爆破的影响越大。要加强爆破点附近的衬砌条件，同时选用的台阶法能够降低爆破振动所产生的影响。