改进的类电磁机制算法及其在FIR数字滤波器中的应用
2018-10-11胡晓朋田雨波许永秀李双双
胡晓朋, 田雨波, 许永秀, 李双双
(江苏科技大学 电子信息学院,镇江 212003)
现实生活中存在着各种各样的最优化问题,解决实际中复杂、多变的最优化问题成为研究者们研究的热点.长期以来,人们受到大自然和生活的启发,一直在不断探索并研究最优化方法.在该领域中,具有重要意义的算法主要包括了遗传算法[1]、粒子群优化算法[2]等.类电磁机制(electromagnetism-like mechanism,EM)算法是由S.I.Birbil和S.C.Fang于2003年提出的一种智能优化算法[3].与其它算法相比,EM算法表现出极其强大的全局搜索能力,其优化思想是模拟电磁场中带电粒子之间的吸引-排斥机制,寻优机制简单、收敛速度快.近年来国内外学者在资源分配[4]、医学诊断[5]、电磁学[6]等领域对其进行了广泛的应用研究.但是,标准EM算法的后期,种群中的带电粒子出现“聚集”现象,此时算法易陷入局部极小值.
为此,文中提出了一种改进的类电磁机制(improved electromagnetism-like mechanism,IEM)算法,即引入早熟的判断和处理机制,对陷入早熟状态的带电粒子,迭代时以一定的概率选中进行小波变异,进而克服EM算法在搜索后期易陷入局部最优的缺陷.
1 类电磁机制(EM)算法
利用EM算法求解无约束函数优化问题的步骤如下:
(2) 局部搜索.对当前xbest进行局部搜索.一旦找到优于xbest的粒子则停止搜索,否则需完成预先设定的迭代次数,并且保持种群不变.
(3) 计算电荷量和合力.EM算法中,电荷量的计算公式为:
i=1, 2,…,m
(1)
之后,计算每个粒子所受的合力.仿照库仑定律的定义方式,带电粒子xi所受合力的计算公式如下:
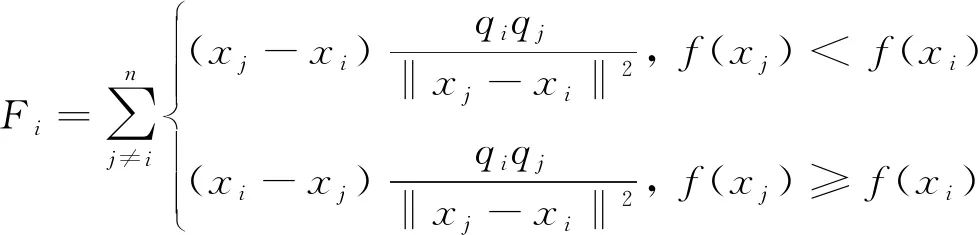
(2)
(4) 移动粒子.对于当前带电粒子xi(i=1, 2,…,m),将其沿着受力方向移动.
(3)
式中:λ∈(0,1)为随机数.移动过程中,其可行移动范围由向量RNG=(v1,v2,…,vD)给出.向量RNG的分量表示对应的朝上下边界移动的可行范围.且有
(4)
如果移动后的粒子目标函数值更优,则用新粒子替换当前粒子,否则保持不变.这样更新了种群中全部带电粒子的位置后,EM算法的迭代也完成了一次.
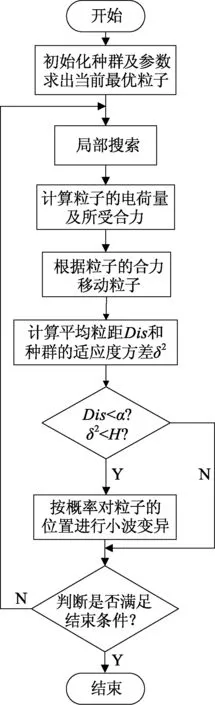
2 改进的类电磁机制(IEM)算法
2.1 早熟判断与处理机制
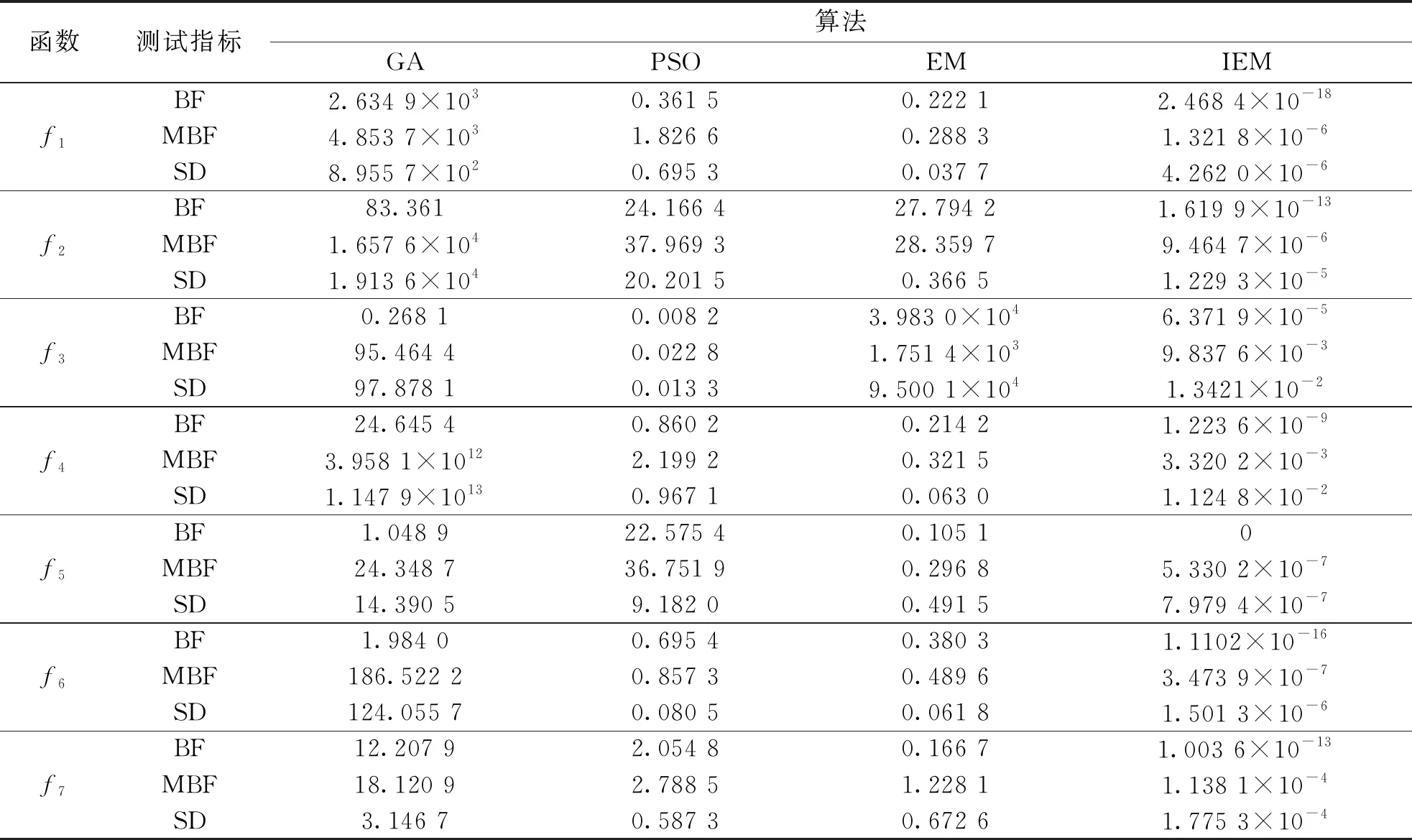
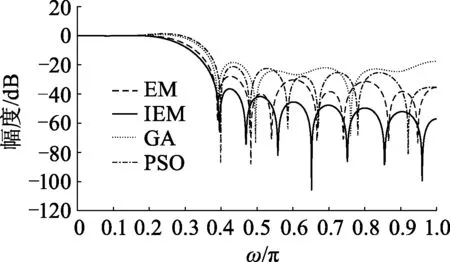
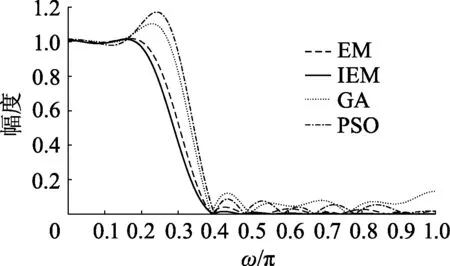
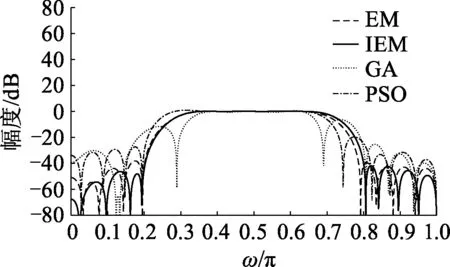
类电磁算法运行到后期,带电粒子容易出现“聚集”现象,导致收敛陷于停滞.文献[7]给出了算法发生早熟收敛的判断依据:当平均粒距Dis<α,且种群的适应度方差δ2 (5) 另外,粒子的位置决定粒子的适应度,可用所有粒子适应度的动态变化去判别种群的现状(是否过于聚集导致早熟收敛),对其进行实时监控.群体适应度方差为: (6) 式中:m为种群大小,fi为粒子i的适应度.favg为当前所有粒子的平均适应度,F为归一化因子,由式(7)确定: (7) 群体适应度方差表示的是粒子间的聚散程度.算法迭代次数增加,不同粒子的适应度越来越接近,δ2也会变小.当δ2 小波是目前数学和工程学科中一个快速发展的领域[8].其中,Morlet小波由于其更为精确、更高分辨率的谱估计,已经被广泛应用于各领域.相对于其他改进的EM算法中使用的高斯变异[9]和柯西变异[10],Morlet小波函数产生正负数的概率是相同的,因此更能有效地在可行域内进行搜索. 文献[11]给出基于小波变异的粒子群优化算法.通过小波变异,粒子偏离当前位置,大大丰富了已有的搜索信息,使粒子有机会向更优的搜索区域移动.引用以下变异公式对EM算法中的带电粒子进行变异: (8) (9) 式中:当a=1时,Morlet小波函数的99%的能量都包含在[-2.5,2.5]区间中,所以φ取值范围区间为φ∈[-2.5a,2.5a]中的伪随机数.a为尺度参数,其计算公式为: (10) 式中:ξwm为单调递增函数的形状参数,gwm为a的上限值,t为当前迭代次数,T为最大迭代次数. IEM实现步骤如下: 步骤1 设置相关参数,种群粒子初始化. 步骤2 局部搜索. 步骤3 根据式(1)和式(2)计算每个粒子的电荷量qi及所受合力Fi. 步骤4 根据式(3)更新粒子位置. 步骤5 根据粒子的适应度函数值,计算平均粒距Dis和种群的适应度方差δ2,并判断Dis<α且δ2 步骤6 按概率对粒子位置进行小波变异. 步骤7 判断算法是否达到最大迭代次数,若满足则输出全局最优位置和其适应度值,算法结束;否则返回步骤2. IEM算法流程如图1. 图1 IEM算法流程Fig.1 Flowchart of IEM algorithm 为了验证IEM算法的优越性,将其与遗传算法(genetic algorithm,GA)、粒子群(particle swam optimization,PSO)算法以及标准EM算法进行对比.选取7个经典高维测试函数作为测试对象[12],其初始化信息如表1,涉及单峰、多峰、无穷极小、非凸病态等多种特性,能有效地考察算法的执行能力. 表1 测试函数基本信息度Table 1 Information of benchmark functions 分别用GA算法、PSO算法、标准EM算法和IEM算法优化上述7个测试函数,算法独立运行30次,记录30次优化后的最优适应值(best fitness,BF)、平均最优适应值(mean best fitness,MBF)及标准差(standard deviation,SD).具体参数设置为:维度30,种群数量50,最大迭代次数1 000,搜索范围列于表1,GA算法遗传算子分别为比例选择、单点交叉和单点变异,设交叉概率为0.7,变异概率为0.1;PSO算法设权重为1,学习因子c1=c2=2;IEM算法设小波变异概率pm=0.2,形状参数ξwm=0.5,尺度参数的上限值gwm=1 000. 从表2最优适应值和平均最优适应值可以看出,对于Sphere函数、Schwefel函数、Griewank函数和Ackley函数,IEM算法求解的精度均提高了8个数量级以上.对于非凸病态函数Rosenbrock函数,其他算法都陷入早熟,只有IEM算法找到了理想的解,IEM算法在Quadratic函数的求解精度上有一个数量级的提高.对于Rastrigrin函数,IEM算法甚至多次找到它的全局最优值.另一方面,标准差值反映出算法稳定性的信息,因此,4种算法中IEM算法稳定性最好. 表2 测试函数仿真结果对比Table 2 Comparison of the optimization for benchmark functions 设N阶FIR数字滤波器的单位取样响应为h(0),h(1),…,h(N-1),其传递函数可表示为[13]: (11) 取z=ejω,则滤波器的频率响应为: (12) 若设FIR数字滤波器理想频率响应为|Hd(ejω)|,则在离散点{ωi|i=1, 2,…,M}上,所设计滤波器的幅度|H(ejω)|与理想滤波器的幅度|Hd(ejω)|的误差平方和为: (13) 将式(12)代入式(13),可得: (14) FIR滤波器要选取滤波器系数h(0),h(1),…,h(N-1)使目标函数E最小,可以用EM算法来求解.采用式(14)作为FIR滤波器设计的适应度函数.即: (15) 显然Fitness值越小,得到的滤波器性能就越好.算法运行结束后,适应度值最小的带电粒子所对应的参数值就是需要求解的滤波器系数. 数字滤波器采用文中所提出的算法进行仿真实验设计,由于高通滤波器设计过程类似于低通滤波器,带阻滤波器设计过程类似于带通滤波器,故此处仅设计低通滤波器和带通滤波器.GA算法、PSO算法、EM算法与IEM算法分别运行20次取平均值作为最后结果.具体参数设置如下:种群数量50,最大迭代次数1 000.GA算法遗传算子分别为比例选择、单点交叉和单点变异,交叉概率0.7,变异概率0.1;PSO算法中权重为1,学习因子c1=c2=2;IEM算法中小波变异概率pm=0.2,形状参数ξwm=0.5,尺度参数的上限值gwm=1 000.例1中4种算法的仿真结果如图2、3,例2中4种算法的仿真结果如图4、5. 例1:设计一个阶数N为21,阻带最小衰减为20 dB的低通数字滤波器,技术指标为: (16) 例2:设计一个阶数N为32,阻带最小衰减为30 dB的带通数字滤波器,技术指标为: (17) 图2 FIR低通数字滤波器对数幅频响应Fig.2 Logarithmic amplitude-frequency curves of low pass FIR digital filters 图3 FIR低通数字滤波器幅频响应Fig.3 Amplitude-frequency curves of low pass FIR digital filters 图4 FIR带通数字滤波器对数幅频响应Fig.4 Logarithmic amplitude-frequency curves of band pass FIR digital filters 图5 FIR带通数字滤波器幅频响应Fig.5 Amplitude-frequency curves of band pass FIR digital filters 由图2可以看出,除了GA算法,其他3种算法设计的FIR低通数字滤波器的阻带衰减都能满足设计要求,但利用IEM算法设计的FIR低通数字滤波器的阻带特性均匀变化,阻带最小衰减比EM算法提高了近10 dB.由图4可以看出,GA算法和PSO算法设计的FIR带通数字滤波器未能达到设计指标,EM算法和IEM算法设计的FIR带通数字滤波器表现良好,并且IEM算法对应的阻带最小衰减比EM算法略有提升.由图3、5可以看出,IEM算法设计的FIR数字滤波器通带波动更小、比较平缓,阻带的波纹几乎为零,更接近理想滤波器. (1) 针对标准EM算法存在早熟收敛的缺陷,提出一种改进的EM算法,引入早熟的判断和处理机制,迭代时以一定的概率选中陷入早熟状态的带电粒子进行小波变异,使其跳出局部最优值. (2) 将文中算法应用于高维测试函数的求解,结果表明该方法在应对高维复杂化问题时具备较强的开发能力. (3) 相较标准EM算法,应用文中算法设计的FIR数字滤波器得到了更为满意的仿真结果,说明其具有良好的参考价值.
2.2 小波变异策略
2.3 IEM算法步骤
2.4 数值验证实验

3 FIR数字滤波器的设计
3.1 FIR数字滤波器介绍
3.2 FIR数字滤波器仿真实例
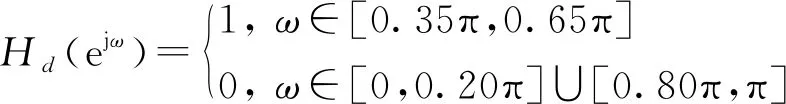

4 结论
