好题多解 益处多多

吴婧怡

(河北省乐亭第一中学 063600)

一道好题往往可以从多角度、多方位进行思考，虽然解题的思路、方法有所不同，但获得的答案是相一致的，多解问题可以激发我们的学习灵感，有利于我们的思维开阔.另外，对同一问题采用多种方法进行分析研究，也有利于我们充分认识问题本质，加深对所学知识的理解.

一、考题呈现，引出下文

在△ABC中，AB=AC，AC边上的中线长度为9，当△ABC的面积最大时，AB的长度为( ).

本题主要考查三角形基础知识，需要我们充分利用三角形的相关定理、公式来解决，同时几何问题对我们的识图能力也要求较高，需要我们从中提炼基本图形，运用基础知识来解决.本题属于中等难度的试题，可以通过多种方法解决，我们要充分利用该类多解题，尤其是在备考阶段，合理利用可以起到事半功倍的学习效果.

二、不同角度，解决问题

1.巧用中线，计算面积

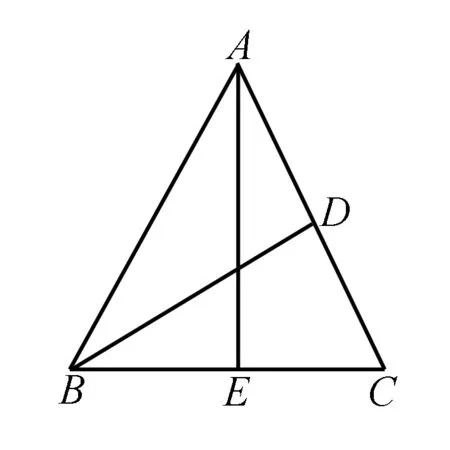
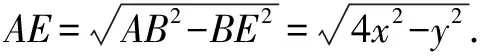
评注上述解题过程主要利用的是三角形的中线长公式，得到了x与y的关系，再利用等腰三角形的中线，即垂线的性质，进一步得到三角形的面积表达式，最后结合基本不等式，得到了另一个x与y的等量关系.

2.突出重心，利用性质

评注上述解题过程，联想到了BD与AE的交点G恰好为△ABC的重心，所以可以利用三角形的重心性质，因此我们可以在直角三角形GEB中设出关于边长的未知数x和y，再利用基本不等式求出三角形面积取得最大值时的AB长.

3.直角坐标，事半功倍

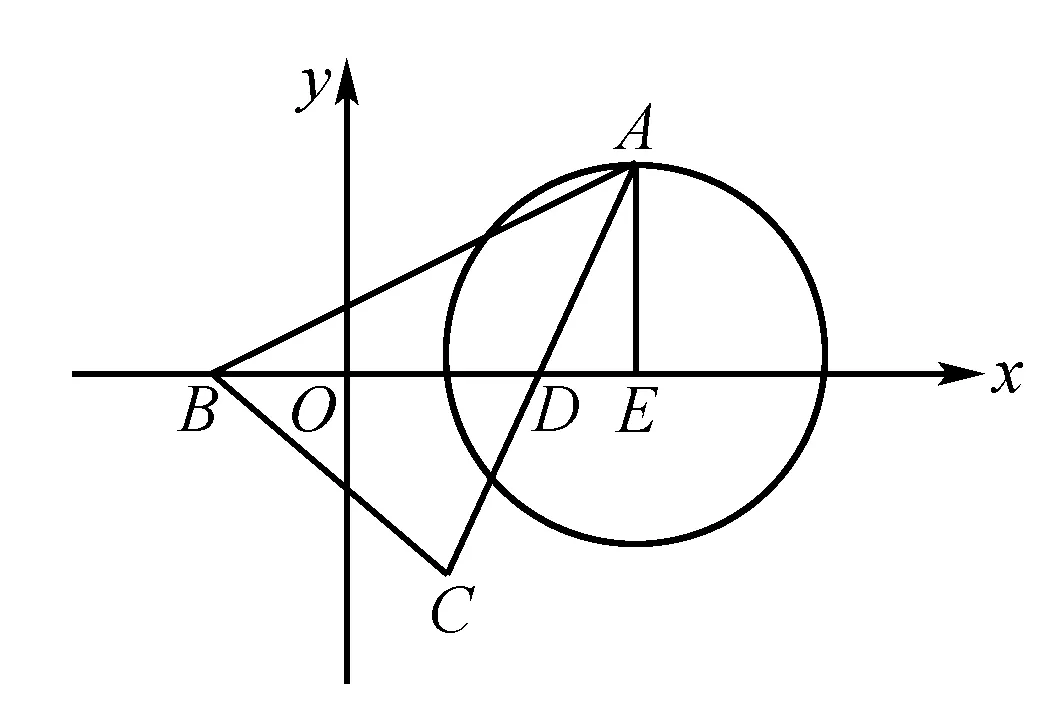
评注我们在求解平面几何问题时，采用构建平面直角坐标系的方法可以将几何条件坐标化、参数化，并通过各点的坐标值建立起相应的等量关系，有利于后续的数形结合分析，因此该种方法可以极大的简化解题步骤.

三、总结提高

好题多解，即从不同的角度来分析同一问题，并利用我们所学的知识，充分挖掘已知条件与结论之间的关系，然后利用不同的方法求解问题答案，多解的学习过程，可以有效锻炼我们的解题思维.另外对不同的解法进行分析比较，可以使我们深刻认识问题的本质所在，而探寻问题的最优解法，潜移默化中就可以提高我们的解题能力.