一类时滞Lipschitz非线性离散广义系统观测器的设计
2018-10-10孙延修黎虹潘斌
孙延修,黎虹,潘斌
(1.沈阳工学院基础课部,辽宁 抚顺 113122;2.辽宁石油化工大学理学院,辽宁 抚顺 113001)
1 引言
广义系统广泛存在于社会生产的各个领域,如:机器人系统、电力系统、电子网络等.事实上,实际存在的广义系统往往带有时滞,如:神经网络、化学反应系统等.随着计算机的快速发展及时滞系统的广泛应用,针对广义时滞系统的研究具有了一定的积极意义.状态反馈是系统控制的一个重要手段,观测器在控制系统中具有一定的应用性.针对系统观测器的研究,文献[1-4]中对非线性广义系统的观测器进行了设计,文献[5]通过利用反馈增益矩阵对Lipschiz非线性广义系统的观测器进行了设计,文献[6]在状态变量不完全可获得时,利用线性矩阵不等式方法针对离散时滞非线性广义系统的观测器进行了设计,并且将结果推广到系统方程含有不确定性的情形,文献[7-9]中针对具有实际应用的时滞系统如神经网络、人口动力学模型以及化学反应系统等进行了描述,文献[10]通过将带有非线性项的矩阵不等式转化为两步线性矩阵不等式的方法,针对时滞Lipschitz离散非线性系统的全维和降维观测器进行了设计,解出了观测器的两个增益矩阵并给出观测器存在的充分条件,从而丰富了时滞系统观测器设计与研究的方法.
目前,针对正常系统观测器的研究已经取得了很大发展,时滞系统具有重要的实际应用意义,对时滞系统观测器的研究也有了一些成果,而针对离散广义时滞系统观测器的研究相对较少,可以作为进一步研究的方向.本文基于离散时滞系统观测器的设计与研究,针对一类时滞Lipschitz非线性离散广义系统的观测器进行设计并给出了观测器存在的充分条件,最后利用数值算例验证了观测器设计的可行性.
2 问题描述
考虑如下时滞广义系统:
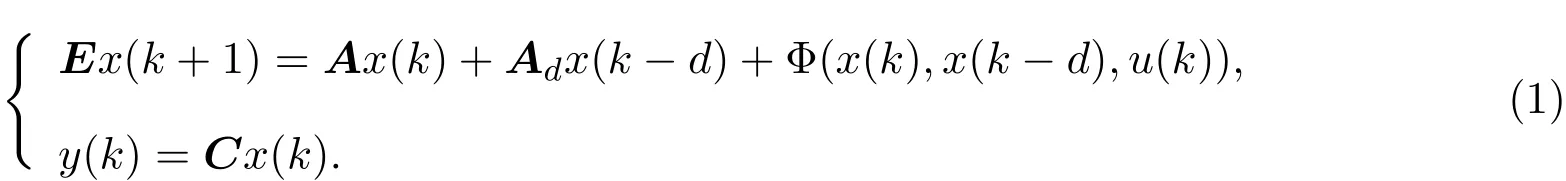
其中,E∈Rn×n为奇异矩阵且满足rank(E)=q 为常数矩阵;u∈Rm,y(k)∈Rp分别是系统的状态,输入和输出. 假设 2.1 系统的非线性项Φ(x(k),x(k−d),u(k)),满足Lipschitz条件,即有 其中,LΦ为大于0的Lipschitz常数. 定义 2.1 根据n个采样周期内采样到的输入u(k)和输出y(k),能唯一地确定系统的状态x(k),则称系统可观测. 本文的目标: (I)当系统的非线性项等于零时,根据假设2.2系统(1)转化为: 设计如下状态观测器: 令e(k)=x(k)−ˆx(k),则由观测器(3)与系统(2)得到的误差系统(4)是渐进稳定的: (II)当系统存在满足Lipschitz条件的非线性项时,根据假设2.2,系统(1)转化为: 设计如下状态观测器: 令e(k)=x(k)−ˆx(k),则由观测器(6)与系统(5)得到的误差系统(7)是渐进稳定的: 其中 根据线性矩阵不等式的方法,考虑时滞广义系统的观测器设计及误差系统的稳定性问题. 定理 3.1 若存在对称正定矩阵P,Q和增益矩阵L,Ld满足下列不等式,则(3)式为系统(2)的观测器: 其中,P,Q为对称正定矩阵,¯A=TA−LC,¯Ad=TAd−LdC,∗表示对称矩阵中的对称部分. 证明设e(k)=x(k)−ˆx(k),则由系统(2)和观测器(3)可得误差系统为: 选取李雅普诺夫函数: 故有 其中 根据schur补引理,矩阵M1<0等价于定理中的矩阵不等式(8),故∆V<0误差系统渐进稳定,定理得证,即(3)式为系统(2)的观测器. 定理 3.2 若存在对称正定矩阵P,Q和增益矩阵L,Ld满足下列不等式,则(6)式为系统(5)的观测器: 其中,P,Q为对称正定矩阵,α,β=∥T∥LΦ为大于零的实数,¯ P=P+αβ2I,∗表示对称矩阵中的对称部分. 证明设e(k)=x(k)−ˆx(k),则由系统(5)和观测器(6)可得误差系统为: 记 选取李雅普诺夫函数: 由于Φ(x(k),x(k−d),u(k))满足Lipschitz条件,知 故有 其中 根据schur补引理,矩阵M2<0等价于定理中的矩阵不等式(9),故∆V<0误差系统渐进稳定定理得证,即(6)式为系统(5)的观测器. 注 3.1 上述两个定理中李雅普诺夫函数的构造具有一定的相似性,基于定理3.1中李雅普诺夫函数的构造方法,定理3.2考虑到了系统所具有的Lipschitz非线性项选取了类似的李雅普诺夫函数,给出了时滞Lipschitz非线性离散广义系统观测器存在的条件. 例 4.1 考虑时滞离散广义系统(1)的参数如下: 系统(1)可以转化为(5)式的形式,根据文献[10]中针对增益矩阵利用线性矩阵不等式的求解方法可以计算得出观测器的增益矩阵: 本文主要研究了一类时滞Lipschitz非线性离散广义系统观测器的设计问题.基于时滞离散广义系统的特殊结构,利用线性矩阵不等式的方法分别设计出了系统在无Lipschitz非线性项条件下的状态观测器以及系统存在Lipschitz非线性项条件下的状态观测器,根据schur补引理给出了Lipschitz非线性系统观测器存在的条件,实现了系统与观测器的误差系统渐进稳定并有利于观测器增益矩阵的求解.最后,数值算例验证了非线性时滞广义系统观测器设计方法的可行性.针对带有外部干扰及不确定性的广义时滞系统观测器的设计则可以作为今后进一步研究的方向.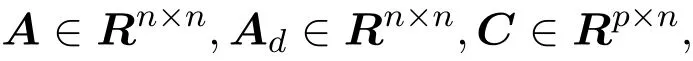
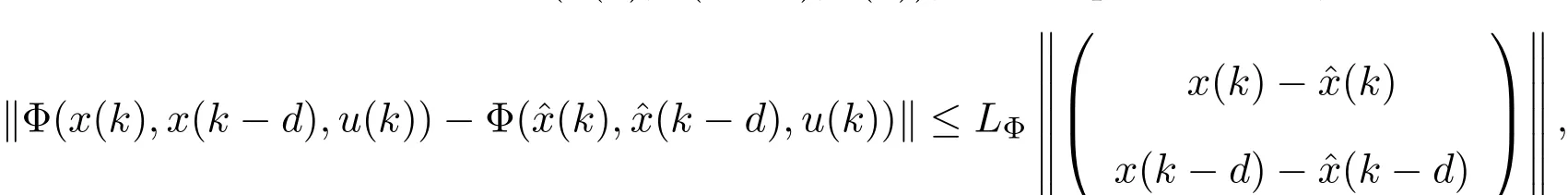
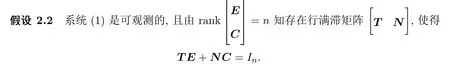
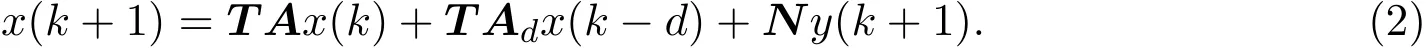
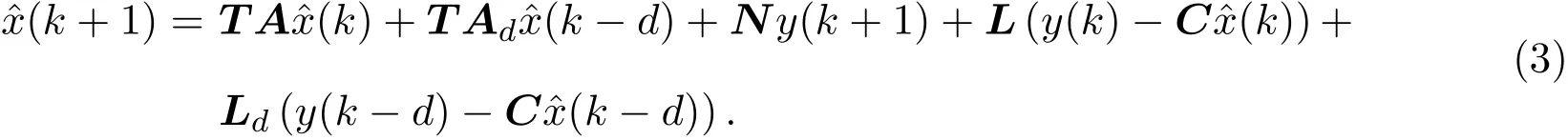
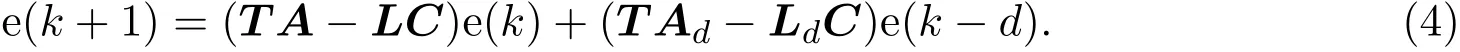
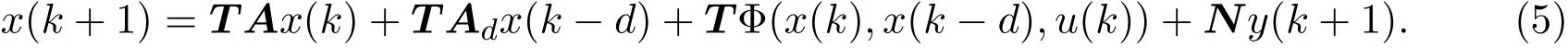

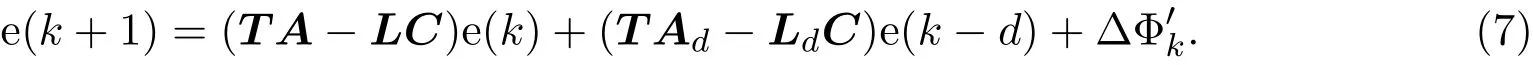
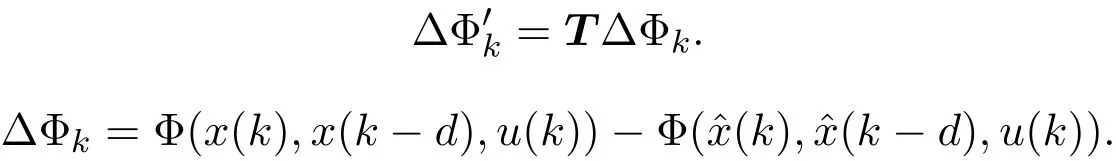
3 主要结果

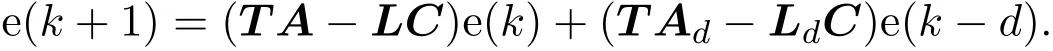
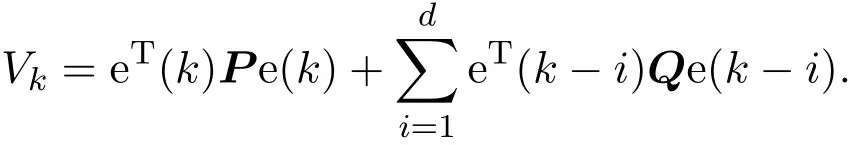
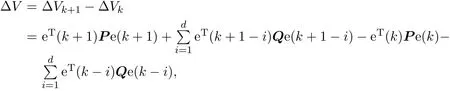
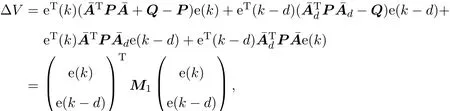
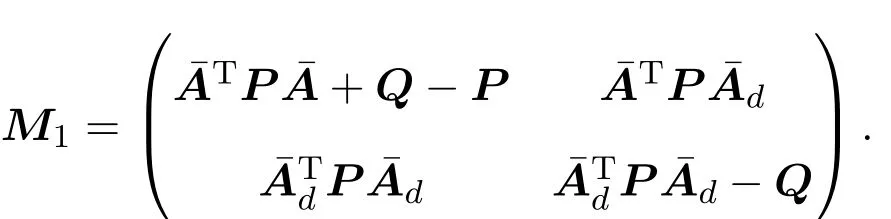
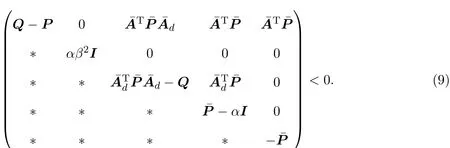
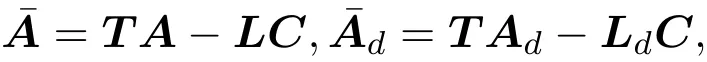


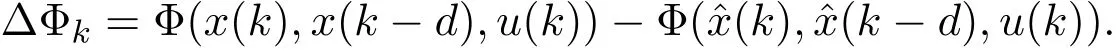
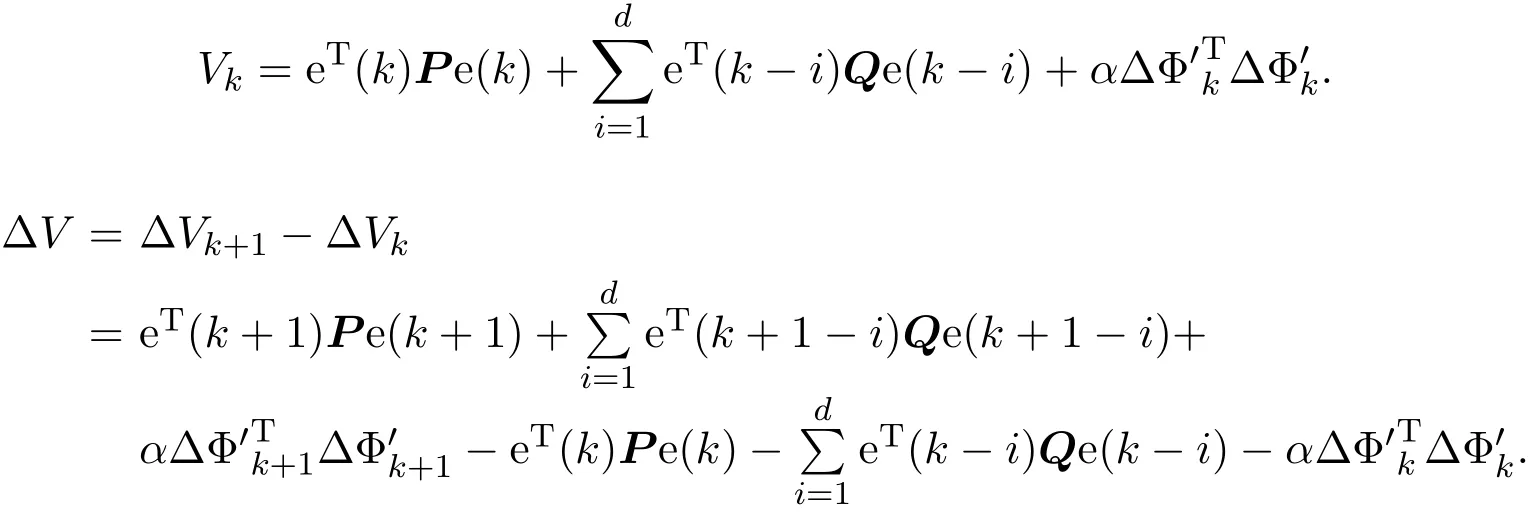


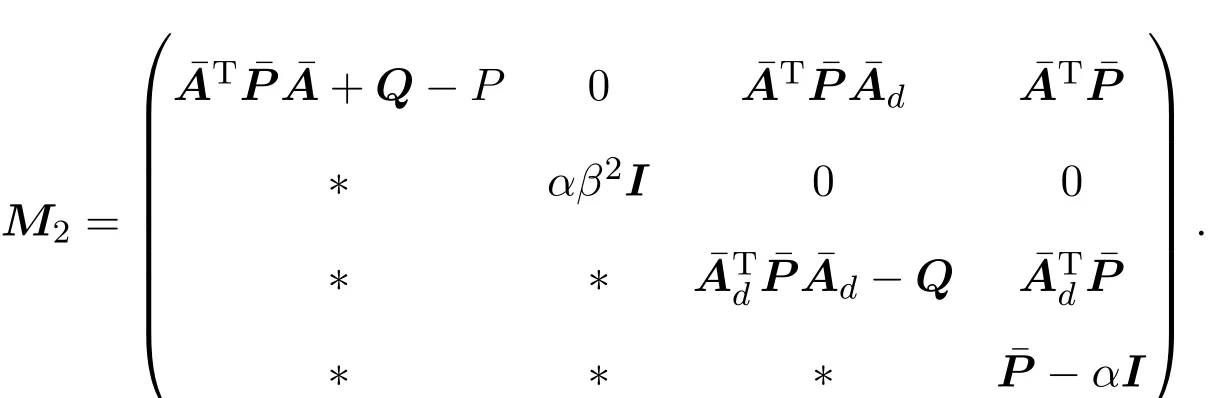
4 数值算例

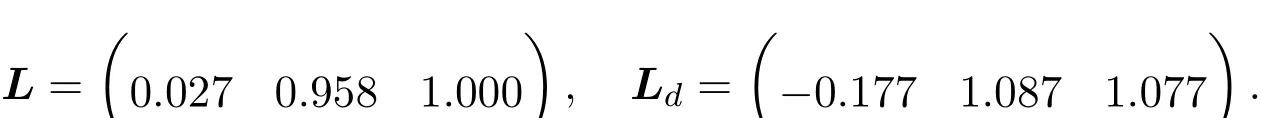
5 结论
