基于AMD的信号趋势项提取和应用

徐洪俊　吴杰　张其林

摘要： 研究基于解析模态分解（analytical mode decomposition， AMD）法的信号趋势项提取方法，将趋势项定义为满足一定频率限值的信号分量，并探讨AMD的端部效应。对比AMD和经验模态分解（empirical mode decomposition， EMD）法的数值模拟与实测数据结果，验证该方法的可行性。分析结果表明：AMD法和EMD法对于趋势项的提取都具有很好的适用性，无须事先假定趋势项类型；与EMD法相比，AMD法处理长时间数据的效率更高。

关键词：振动信号； AMD； EMD； 信号趋势项

中图分类号： TU317； TP391.77

文献标志码： B

Abstract：Signal trend extraction technique based on Analytical Mode Decomposition（AMD） is studied. The trend item is defined as a signal component which meets the limit of the specified frequency， and the end effects of AMD are discussed. The feasibility of the AMD method is verified by comparing the results of numerical simulation and measured data based on AMD method and Empirical Mode Decomposition（EMD） method. The results show that the AMD method as same as the EMD method has good applicability for the trend extraction， and they all need not to assume the original types of trend items.The AMD method is more efficient than the EMD method on the aspect of processing long time data.

Key words：vibration signal； AMD； EMD； signal trend item

0 引 言

在数据采集中，温度变化会导致零点漂移、传感器频率表范围外低频性能不稳定等，进一步可能导致实测数据偏离真实值基线，甚至偏离大小会随时间变化。这种在随机信号中存在的常数项或者缓慢变化的、周期大于记录周期长度的成分被称为信号的趋势项。[1]数据的平稳性假设是很多数据分析方法的前提条件，但在数据分析中，观测数据含有潜在的趋势项会造成数据不平稳，给时域分析和频域分析带来较大的误差，严重影响频谱分析中低频段的真实性，对二次积分的数据影响更大。[2]然而，有些信号中的趋势项具有明确的物理含义，例如风压数据中的趋势项被认为是风压的平均分量，风速、风向数据中的趋势项被认为是风速、风向的平均分量，因此，趋势项的提取对于数据分析具有十分重要的意义，尤其是具有明确物理意义的趋势项更加重要。

很多趋势项提取方法需要预先假定趋势项的类型，不具备良好的适用性。经验模态分解（empirical mode decomposition， EMD）法[3]在趋势项提取中得到广泛的应用，但EMD法在工程应用中存在以下问题：不能分解紧密间隔频率成分的信号；很难区分窄带信号中的各种成分；不能从大的波动中分离出小的间歇性波动；长时间的实测数据分解产生大量的固有模态函数（intrinsic mode function， IMF）、消耗大量时间。[4]针对此问题，本文采用解析模态分解（analytical mode decomposition， AMD）法提取信号中的趋势项，并研究其对不同类型趋势项[4-6]的适用性。

2 基于AMD的趋势项定义和AMD端点效应处理

信号中的趋势项一般是指信号中周期大于记录长度的成分。[1]在实际应用中，信号中的趋势项往往很复杂，例如在桥梁或者高层建筑的风振响应分析中，风速中远大于结构基本周期的所有分量均可视为风速平均分量。考虑实际的工程应用和AMD法的使用，借鑒XU等[7]对趋势项的定义，将小于指定频率fc并由式（2）获得的信号分量x1（t）定义为AMD法的趋势项。fc根据数据要求设置，如风场非平稳分析中，要求fc小于结构第一自振频率。

AMD法提取的某线性趋势项见图1。AMD法仍然存在类似EMD法的端部效应。与EMD法中端部极值点不精确和希尔伯特变换导致的端点效应[8]相比，AMD法的端点效应是由于三角正交基和希尔伯特变换造成的。三角正交基是AMD法提取的线性趋势包含波动的主要因素。由式（2）可以看出，虽然AMD法在信号分解时仅仅调用2次希尔伯特变换，但仍然存在由于傅里叶变换造成端点处频率泄漏的不利影响，尤其是在提取线性趋势项时会在端部产生很大的误差。AMD法的端点效应可以采用与EMD法相同的办法处理，本文中采用镜像延拓[9]处理方法。数据的镜像延拓可抑制希尔伯特变换的不利影响。

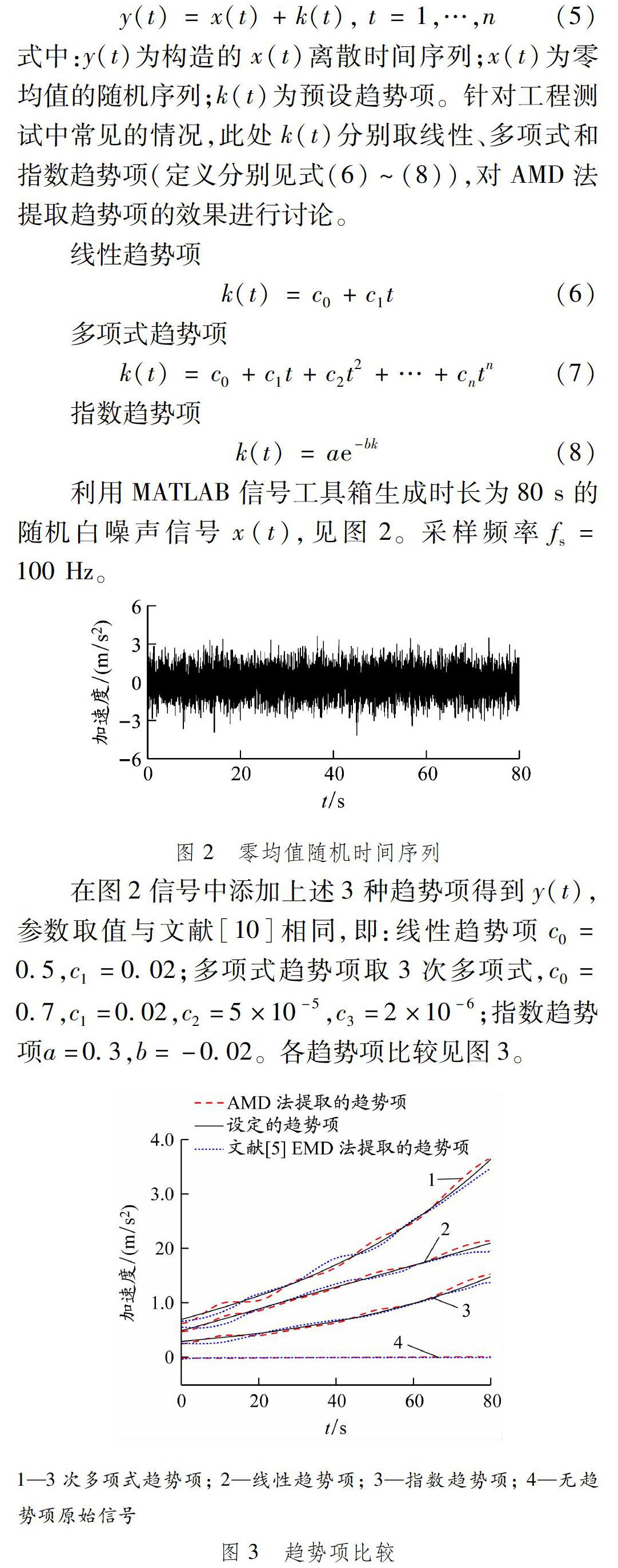
图3中的虚线4是图2中的时程曲线，即x（t）不包含任何趋势项时的情况。由此可以看出：当信号中没有趋势项时，用AMD法提取出的趋势项近似为0，与实际情况相符。对于趋势项为线性、多项式和指数型时，利用AMD法提取出的趋势项与设定的趋势项吻合，并且与文献[5]中运用EMD法得到的趋势项相接近。去趋势项的数据全都可通过逆序检测[1]，表明AMD法可以有效地提取数据潜在的趋势项。因此，AMD法与EMD法一样，无须预设趋势项类型也能够有效提取数据的趋势项，具有良好的适用性。

3.2 实测应变和风压监测数据分析

2016年9月13日某高铁站实测应变监测数据见图4a），总时长24 h，采集时间间隔60 s。分别采用AMD法和EMD法对应变时程数据提取趋势项，结果见图4b）。从图中可以看出，由AMD法和EMD法提取的趋势项都能够很好地反映数据的潜在趋势，并且两者提取的趋势项十分接近。另外，经AMD法和EMD法去趋势项的数据都可通过逆序检测，表明2种方法均能够有效提取数据的趋势项。从数据分解的时间来看，AMD法用时0.014 s，EMD法用时0.059 s，可见AMD法的效率较高。

2017年6月5日上海中心实测风压数据见图5a），总时长300 s，采样频率为100 Hz，风压存在明显的阶跃突变。分别采用AMD法和EMD法对应变时程数据提取趋势项，结果见图5b），去趋势项的实测风压时程数据见图6。

由此可以看出：AMD法和EMD法提取的趋势项都能够很好地反映数据的潜在趋势，并且两者提取的趋势项十分接近。经AMD法和EMD法去趋势项的数据都可以通过逆序检测，表明2种方法均能够有效提取具有阶跃突变的趋势项。AMD法数据分解用时0.226 s，EMD法用时50.201 s，再次证明AMD法的效率较高。

3.3 AMD法与EMD法计算效率对比

为进一步比较AMD法和EMD法的计算效率，分别利用2种方法对不同时长的数据进行处理。计算数据采用2017年6月5日在上海中心顶部（距离地面约600 m）实测的风速数据，数据样本时长从100 s到3 600 s，样本时间间隔为100 s，共计36份，采样频率均为100 Hz。时长3 600 s的实测风速数据和2种方法提取的趋势项见图7。由此可以看出：2种方法提取的趋势项均可以很好地反映样本的变化趋势。

分别采用AMD法（fc=1/120 Hz）和EMD法（以固有模态函数的前5项之和为信号的趋势项）对不同时长的数据样本提取趋势项，所耗时间对比见图8。随着数据样本的增加，AMD法耗时稳定且小于0.8 s，EMD法耗时随样本数量的增加而快速增加，尤其是1 h的数据计算耗时达到 851.1 s。对于处理900 s（15 min）以上数据，EMD法的耗时是AMD法的400倍以上。这是由于数据量的增长加剧EMD法的筛选过程[3]，而AMD法相当于在频域范围内对数据进行1次二分法的分割，所以计算时间大大减少。由此可见，AMD法比EMD法在效率上有明显优势，在实际应用中可以避免处理长时段数据时因截断而引起的频谱波动。

4 结 论

AMD法在本质上是利用希尔伯特变换分解具有特定频率成分的信号，相当于一个自适应的低通滤波器。与传统的低通滤波器相比，AMD法可以精确提取信号的超低频项[11]，比如提取频率0.1 Hz左右的信号，或者更低加速度的信号。目前，EMD法是趋势项提取的主流方法，但在实际应用中EMD法存在计算效率低下的缺陷，因此，本文采用AMD法提取模拟和实测信号中的趋势项，并与EMD法进行对比分析，结果表明：

（1）AMD法与EMD法一样，无须预设趋势项类型和分解函数基，具有良好的适用性。

（2）AMD法与EMD法均能够有效提取信号中的趋势项，均存在指定频率fc的选取问题。

（3）AMD法的计算效率比EMD法的计算效率具有明显的优势。对于不小于15 min时长数据的趋势项提取，EMD法的耗时达到AMD法耗时的400倍以上。在实际工程中，针对长时间段的采样数据（如台风记录时长一般在17～35 h），利用EMD法会产生大量的硬件和时间消耗，对数据的截断分批处理还会引起频谱波动，而AMD法能够快速有效地处理长时段数据，避免长时段数据在处理时由于截断而引起频谱波动。

参考文献：

[1] BENDAT J S， PIERSOL A G. Random data： Analysis and measurement procedures[M]. New York： John Wiley & Sons， 1986： 396-398.

[2] 高品贤. 趋势项对时域参数识别的影响及消除[J]. 振动、测试与诊断， 1996， 14（2）： 20-26.

[3] HUANG N E， SHEN Z， LONG S R， et al. Empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of Royal Society of London： Series A， 1998， 454： 903-995.

[4] CHEN G， WANG Z. A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components[J]. Mechanical Systems and Signal Processing， 2012， 28（2）： 258-279. DOI： 10.1016/j.ymssp.2011.02.002.

[5] 时培明， 苏翠娇， 韩东颖. 基于AMD-HHT的非平稳信号紧密间隔频率检测[J]. 仪器仪表学报， 2014， 35（12）： 2817-2825.

[6] 郑近德， 潘海洋， 程军圣. 非平稳信号分析的广义解析模态分解方法[J]. 电子学报， 2016， 44（6）： 1458-1464.

[7] XU Y L， CHEN J. Characterizing nonstationary wind speed using empirical mode decomposition[J]. Journal of Structural Engineering， 2004， 130（6）： 912-920.

[8] 贺智， 王强， 沈毅， 等. 希尔伯特-黄变换端点效应抑制算法综述[J]. 软件， 2011， 32（10）： 1-7.

[9] HUANG D， ZHAO J， SUN J. Practical implementation of Hilbert transform algorithm[J]. Acta Oceanologica Sinica， 2003， 22（1）： 1-14.

[10] 陳隽， 徐幼麟. 经验模分解在信号趋势项提取中的应用[J]. 振动、测试与诊断， 2005， 25（2）： 101-104.

[11] 李晶， 曹登庆， 刘绍奎， 等. 基于解析模态分解和希尔伯特变换的模态参数辨识新方法[J]. 振动与冲击， 2016， 35（1）： 34-3.

（编辑 武晓英）