机器人加工的映射一致性建模及加工实验研究

冯亮友，梁志鹏，席文明

(厦门大学航空航天学院，福建厦门361005)

与计算机数控(CNC)加工装备封闭式体系结构不同，机器人体系结构具有开放性，能够与不同对象集成而形成加工系统，实现对大尺寸雕塑、复杂曲面零件、飞机组装中的铆钉孔等的加工[1-5]，弥补CNC加工装备体系结构的不足，降低加工成本.为了提高产品加工精度以及编程效率，降低装备的操控和使用难度，机器人加工装备需要采用计算机辅助设计/计算机辅助制造(CAD/CAM)数字化系统产生加工轨迹[6-9].

采用CAD/CAM数字化系统产生机器人加工轨迹时，形成2个不同的空间，即机器人轨迹生成的CAM空间和机器人进行加工的作业空间.当机器人和加工对象集成后，在CAM空间中，加工对象模型与机器人模型之间的转换矩阵不同于作业空间中二者的转换矩阵.当加工对象模型上的轨迹点由CAM空间映射到作业空间时，由于2个空间中对应的转换矩阵不同而导致轨迹偏差，即CAM空间产生的轨迹不会正确地映射到加工对象上，该轨迹偏差最终形成机器人的加工误差.提高轨迹精度的方法是建立CAM空间与作业空间的映射一致性，即保持2个空间的转换矩阵一致.

现有研究更多地集中在机器人内参数的标定中[10-13]，即几何参数标定.对机器人加工装备的外参数，即CAM空间与作业空间的映射一致性建立，关注并不多.现有建立映射一致性的方法一般首先建立作业空间中各对象之间的转换矩阵模型；其次利用测量仪器测量各自对象上的特征点，并利用优化算法提高特征点的测量精度[14-17]；再次利用测量的特征点计算各个对象之间转换矩阵中的元素；最后，利用计算的转换矩阵调整CAM空间中对应对象的CAD模型位姿，实现2个空间对应转换矩阵的一致性.上述建立映射一致性方法中，测量仪器测量的特征点无法与各个对象的物理坐标系直接关联，特别是无法与机器人基坐标系直接关联，导致建立映射一致性的过程复杂，求取的转换矩阵精度不足.Wei等[14]为了实现测量的特征点与机器人基坐标系之间的关联，通过测量旋转机器人的第一轴上的特征点，利用旋转后特征点拟合的圆，确定第一轴的轴线，从而确定机器人的基坐标系.

本研究直接利用加工装备中的机器人测量加工对象上的特征点，求其位姿，获得加工对象与加工对象模型间的位姿误差，并利用该误差调整加工对象模型的位姿.通过CAM空间机器人运行轨迹点并检测轨迹精度，确定调整位姿误差后的加工对象模型位姿是否与加工对象位姿保持一致.重复测量特征点并检测轨迹精度，实现加工对象模型位姿的递归调整，提高CAM空间与作业空间映射一致性建立的精度.

1 映射一致性

图1中，CAM空间的机器人模型、工作台模型和刀具模型的坐标系分别为∑xbybzb、∑xnynzn和∑xtytzt. 作业空间的机器人、工作台和刀具的坐标系分别为∑XBYBZB、∑XNYNZN和∑XTYTZT.JT1是机器人模型与工作台模型的转换矩阵，JT2为机器人模型与刀具模型之间的转换矩阵，JT3是机器人模型末端第六轴坐标系到刀具模型坐标系的转换矩阵.作业空间中，J1是机器人与工作台之间的转换矩阵，J2是机器人与刀具之间的转换矩阵，J3是机器人末端第六轴坐标系到刀具坐标系的转换矩阵.

图1 CAM空间与作业空间的坐标系系统Fig.1 Coordinate system of CAM space and work space

要建立CAM空间与作业空间的映射一致性，就是要保持两个空间中对应转换矩阵一致，即需要建立以下的关系

(1)

其中，J1、J2、J3、JT1、JT2、JT3为4×4的转换矩阵.假设开始标定前，CAM空间中工作台模型坐标系与机器人模型坐标系重合，作业空间中工作台坐标系与机器人坐标系重合，则

(2)

其中JT0和J0分别为开始标定时CAM空间与作业空间中机器人与工作台之间的转换矩阵.然而，在工作台实际安装时，并不与机器人坐标系重合，即J0和J1不相等，假设作业空间中机器人坐标系依次绕Z、Y和X轴旋转γ、β和α角，再依次沿X、Y、Z轴平移pX、pY、pZ距离得到工作台坐标系，则

J1=J0·R(Z,γ)·R(Y,β)·R(X,α)·T(X,px)·T(Y,py)·T(Z,pz)，

(3)

其中，R(Z,γ)·R(Y,β)·R(X,α)是绕Z、Y、X轴旋转α、β、γ角度的4×4阶位姿坐标转换矩阵，T(X,px)、T(Y,py)、T(Z,pz)是沿X、Y、Z轴平移px、py、pz距离的4×4阶位姿坐标转换矩阵.

欲使CAM空间中工作台模型的位姿与作业空间中的工作台位姿一致，需要对工作台模型的初始坐标系进行旋转和平移.将式(1)和(2)代入式(3)得

JT1=JT0·R(Z,γ)·R(Y,β)·

R(X,α)·T(X,px)·T(Y,py)·T(Z,pz).

(4)

式(4)表明，只要在CAM空间中实现与作业空间中的相同变换，就可以建立2个空间的映射一致性.本质上，CAM空间和作业空间中的同一对象具有位姿调整的可互换性.当工作台安装到作业空间中时，只要测得工作台相对机器人的转换矩阵，就可以利用该矩阵调整工作台模型相对机器人模型的位姿.相反，也可以通过测量工作台模型与机器人模型之间的转换矩阵，然后利用该矩阵调整作业空间中的工作台位姿.与调整模型相比，调整实际对象要困难得多，也无法保证映射一致性建立的精度.由于2个空间中的对象位姿调整具有互换性，下文中，将利用对象模型与对象的位姿误差表示对象模型的位姿误差.

对于机器人末端的刀具，由于存在电主轴连接块的制造和安装误差以及刀具的安装误差，使得J3不等于JT3，导致刀具末端的工具中心点(tool center point，TCP)坐标系产生偏移.在变姿态加工时，不精确的TCP将产生轨迹误差.由于刀具安装在机器人末端，无法直接利用机器人测量J3转换矩阵.在测量J1时，首先在机器人末端安装标定探针，以机器人为基准，标定工作台的位姿.然后，再在机器人末端安装刀具，以标定后的工作台为第二基准，测量机器人第六轴坐标系与刀具坐标系间的转换矩阵J3，即

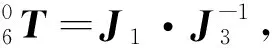
(5)

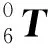
T(X,px1)·T(Y,py1)·T(Z,pz1)，

(6)

其中，R(X,α1)、R(Y,β1)、R(Z,γ1)是绕X、Y、Z轴旋转α1、β1、γ1角度的4×4阶位姿坐标转换矩阵，T(X,px1)、T(Y,py1)、T(Z,pz1)为沿X、Y、Z轴平移px1、py1、pz1距离的4×4阶位姿坐标转换矩阵.

需要注意的是，为了便于刀具模型的调整，需要对刀具(即工作台)相对机器人的第六轴坐标系∑X6Y6Z6进行变换，依据式(5)，可以得到刀具相对第六轴的转换矩阵

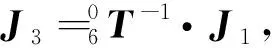
(7)

求出J3后，就可以对刀具模型进行旋转与平移变换，使得JT3=J3.

当机器人末端刀具标定完成后，就可以利用末端刀具测量作业空间中的点，求取对象的位姿，测量的空间点坐标为

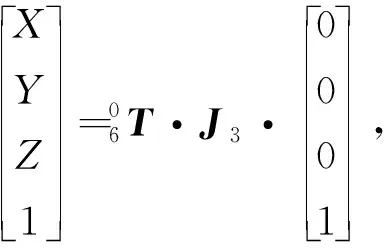
(8)

其中，(X，Y，Z)是空间点的坐标.

为了便于建立2个空间的映射一致性，将标定对象的姿态和位置分开进行求解.假设已知标定对象上的3个点K、L、M的坐标向量为pK、pL、pM，并且这3个点组成一个直角三角形，见图2所示，则可以依据这3个点求得3点所在特征面的姿态，即

图2 映射一致性建立原理Fig.2 The principle to establish mapping consistency

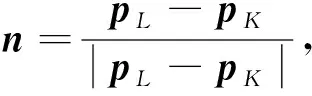
(9)

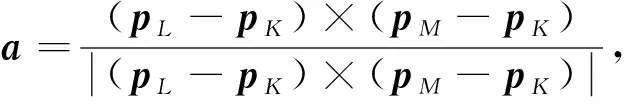
(10)

o=n×a，

(11)

这样，可以得到

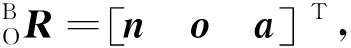
(12)

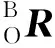
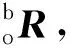
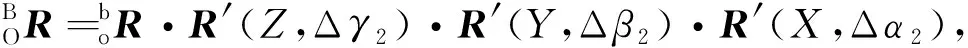
(13)

其中，R′(X,Δα2),R′(Y,Δβ2),R′(Z,Δγ2)是绕X、Y、Z轴旋转Δα2、Δβ2、Δγ2角的姿态坐标转换矩阵.

对于位置标定，建立以下的方程

(14)

式中：I是3×3单位阵；pb是CAM空间中标定对象上的点坐标，pB是作业空间中同一位置点的坐标，为3×1的列向量；Δxb、Δyb、Δzb是沿CAM空间中的特征面坐标系形成的相对坐标系坐标轴的平移距离.在旋转和平移对象模型时，机器人轨迹随模型一起旋转和平移.让机器人再次运行调整位姿后的轨迹点，再次判断机器人末端刀具的顶点与作业空间中的3个点位置误差是否大于设定值，如果轨迹误差大于设定值，则重复上述标定过程，如果轨迹误差小于设定值，则标定结束.

图3 映射一致性实现过程Fig.3 Mapping consistency implementation process

映射一致性本质是求取仿真空间中机器人模型相对作业对象模型的转换矩阵以及作业空间中机器人相对作业对象的转换矩阵，并使这2个对应矩阵相等.例如，在工作台模型上沿两个直角边分别设置x、y坐标轴，并在这2个坐标轴上分别取1个点，从而和∑xyz坐标系的原点构成直角三角形的3个顶点.如果将这3个点映射到作业空间形成轨迹点，机器人运行轨迹点后，其运行轨迹平行于工作台直角边，则工作台模型和工作台之间的姿态一致，而如果运行轨迹不平行于工作台直角边，则需要调整工作台模型的姿态，重新映射轨迹点，直至运行的轨迹平行于工作台直角边.为了便于问题的说明，图3中，在作业空间的工作台上设置参考坐标系∑x′y′z′，其与工作台模型上设置的坐标系∑xyz位姿一致.在仿真空间的模型上取3个点k、l、m，向量pk l与工作台模型坐标系x轴重合，向量pk m与工作台模型坐标系y轴重合.将该3点映射到作业空间形成轨迹点K、L、M，向量PKL与作业空间中X轴重合，向量PKM与作业空间中Y轴重合，如果∑XYZ与参考坐标系∑x′y′z′重合，则完成映射一致性建立，否则调整工作台模型姿态.运行轨迹点后，经测量计算，调整仿真空间工作台，使其绕自身z轴旋转3°.再次将调整后的k、l、m点映射到作业空间，并运行映射的轨迹点，此时参考坐标系的y′轴处于作业空间坐标系的YOZ面内.z轴调整后，再绕y轴旋转2.3°，第3次将调整后的k、l、m点映射到作业空间，并运行映射的轨迹点，此时，参考坐标系的x′轴与作业空间X轴重合.y轴调整后，绕x轴旋转3.5°时，第4次将调整后的k、l、m点映射到作业空间，并运行映射的轨迹点，此时2个坐标系完全重合.实际上，每次调整时存在测量误差，需要重复以上调整过程.再次绕z、y、x轴旋转0.75°、0.36°、0.48°后，2个坐标系间的姿态误差均小于设定值0.02°，至此，工作台姿态调整结束.在标定好姿态的工作台模型上取1个特征点，映射到作业空间中，形成轨迹点，让机器人运行该轨迹点，测量实际轨迹点和理论轨迹点间的位置偏差，即沿工作台坐标轴X、Y、Z的偏差分别为5，-2.5 和3 mm.在仿真空间中，分别沿x、y、z轴移动-5，2.5，-3 mm.再次将调整后的特征点映射到作业空间中，形成轨迹点，让机器人运行该轨迹点，测量实际轨迹点和理论轨迹点间的位置偏差均小于设定值0.2 mm.至此，建立了仿真空间工作台模型与作业空间工作台之间的映射一致性.

姿态转换矩阵以第1次调整为例，由于绕相对坐标系旋转，故旋转矩阵按z、y、x顺序右乘，设绕仿真空间坐标轴z、y、x旋转角度分别为γ、β和α，则由式(13)得：

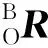
(15)

其中γ、β和α分别为3.5°、2.3°、3°.

由式(14)得位置转换矩阵为：

(16)

其中Δxb、Δyb、Δzb分别为-5，2.5和-3 mm.

2 实验结果

加工系统包括机器人、安装于机器人末端的电主轴、电主轴连接块、电主轴上的刀具、安装雕塑毛坯的工作台、雕塑毛坯、控制系统等，见图4所示.雕塑毛坯的形状为长方体，材料为石膏.

图4 机器人加工系统Fig.4 Robot processing system

由于电主轴连接块制造和安装要求精度高，所以没有对J3矩阵中的平移量进行标定，而是直接利用电主轴连接块的CAD模型参数、刀具尺寸和标定好的姿态设置刀具坐标系(也是TCP坐标系).然后，利用安装了刀具的机器人标定工作台和雕塑毛坯.

采用同样的方法对雕塑毛坯进行标定，由于雕塑毛坯是长方体形状，直接取前侧长方形的两个直角边上的点以及两个直角边的交点作为测量点.同样，经过3次重复标定后，机器人的轨迹误差产生了振荡，此时停止标定.

为了验证映射一致性建立效果，如图5所示在石膏毛坯上加工4组开口通槽，通槽采用双侧加工方法，每侧分别加工通槽的3/5，通过双侧加工后测量不同加工侧槽的错开误差，就可以检测映射一致性建立的精度.通过测量，4组槽侧面的错开误差分别为0.68，0.71，0.73和0.69 mm.

图5 映射一致性精度测量实验Fig.5 Mapping consistency accuracy measurement experiment

完成映射一致性的精度验证后，利用机器人加工装备加工雕塑.如图6所示的雕塑模型，在加工前，利用ArtCAM软件(英国，Delcam公司)产生雕塑加工的刀轨迹，然后将刀轨迹连同雕塑CAD模型一起导入安川机器人的离线编程软件MOTOSIMEG(日本，MotoMan公司)中，利用标定的转换矩阵设置工作台模型以及加工对象模型在CAM空间的位姿，由离线编程软件将刀轨迹转换成机器人加工轨迹.需要注意的是，在采用ArtCAM产生刀轨迹前，需要设置雕塑CAD模型的坐标系，刀轨迹导入离线编程软件时，保持雕塑CAD模型的坐标系和标定完的雕塑毛坯模型坐标系重合，并且雕塑CAD模型被毛坯模型所包含.

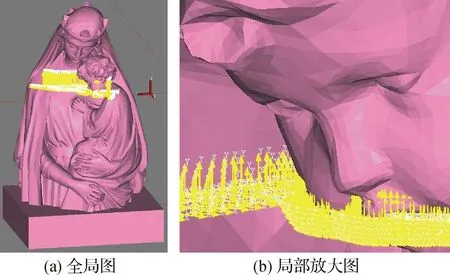
图6 机器人加工轨迹生成方法Fig.6 Robot machining trajectory generation method

该雕塑采用了多侧加工方法，每侧刀轨迹产生方法相同，依据雕塑CAD模型坐标系和雕塑毛坯坐标系重合的条件，将多侧加工的轨迹进行拼合，对雕塑进行完整的加工.图6中只显示了两行转换完成的机器人精加工轨迹.

在利用ArtCAM产生刀轨迹后，对产生的刀轨迹进行了优化处理，使得机器人能够采用最大轮廓法对雕塑进行粗精加工.所谓最大轮廓法就是只保留雕塑CAD模型最大轮廓内部的加工轨迹点，删除最大轮廓外部的加工轨迹点并对抬刀点进行相应处理.这样，当采用多侧加工后，其加工的雕塑和未加工的毛坯自动分离，从而提高加工效率，减少刀具磨损.

由于该雕塑形状复杂，采用机器人左右双侧粗加工和第三侧精加工的多方向加工方法如图7所示，从完成双侧粗加工后的雕塑外形可以看出，在左右侧的加工分界面上，即最大轮廓上，左右侧粗加工部分对准较好(图7(a)).另外，通过测量分离面两侧对应的加工面误差，即最大轮廓两侧对应加工轨迹误差(图7(b))，再次验证映射一致性建立的有效性，其不同加工侧之间的误差为0.72 mm.

(a) 粗加工后的雕塑外形；(b) 粗加工完成后，与雕塑分离的毛坏.图7 粗加工后两侧加工轨迹对准情况Fig.7 The processing path alignment on both sides after roughing

(a) 双侧加工拼合处局部图；(b) 第三侧精加工过渡处局部图；(c) 雕塑全局图.图8 多方位精加工后的效果及加工后的雕塑Fig.8 Multi-directional finishing effect and the sculpture after processing

图8是多方位精加工完成后的雕塑局部和全局图，可以看出左右侧加工拼合处(最大轮廓位置)未产生明显台阶(图8(a)).图8(b)是第三侧精加工结果，主要是婴儿脸部和母亲胸部之间的部分加工，见图6的加工轨迹.由于上述部分形状复杂，在一个很小的区域中，加工近60 mm深度.为了避免干涉，采用了机器人变姿态加工，即在机器人运行加工轨迹时，机器人的姿态连续变化，避免刀具和雕塑的干涉.由于建立映射一致性，能够精确放置TCP坐标系，通过软件仿真后，加工过程没有产生因TCP放置不精确而产生的加工轨迹偏移，其局部加工区域与前期加工区域过渡平滑，其界面上没有明显折线出现.完成加工后的雕塑见图8(c).

3 结 论

本研究利用加工装备中的机器人作为测量工具，建立CAM空间与作业空间映射一致性的数学模型，对CAM空间与作业空间中的各对象之间的转换矩阵进行了标定，实现了2个空间的映射一致性.利用映射一致性建立时的参数对CAD/CAM数字化系统生成的刀轨迹进行转换，产生机器人加工轨迹并对产品进行加工，提高机器人的加工精度.该方法特别适合于在工厂环境中应用，也便于软件算法实现自动化标定.与前期未建立映射一致性的机器人加工装备加工的雕塑比较，其双侧对准误差从20 mm降低到0.7 mm，并且建立映射一致性后，可以精确地放置TCP坐标系，避免变姿态加工时的加工轨迹偏移.

在递归调整对象模型的位姿时，当轨迹精度达到0.7 mm时，再次标定将产生轨迹误差的振荡，无法进一步提高标定精度.轨迹误差产生振荡的原因是机器人存在内参数误差，内参数误差包括机器人几何参数误差和零位误差，使得机器人测量的特征点精度无法提高.未来，将对机器人的内参数进行标定，然后再利用标定了内参数的机器人测量对象上的点坐标，进一步提高映射一致性的精度.