自抗扰控制技术的改进和应用

李家豪，孙洪飞

(厦门大学航空航天学院，福建厦门361005)

自抗扰控制[1](active disturbance rejection control, ADRC)技术吸取了PID算法的优点，采用基于误差消除误差的思想，利用非线性反馈提高控制器效率．该控制方法将系统内部扰动、外部干扰、系统未建模动态以及其他影响视为“总和扰动”，通过扩张状态观测器(extended state observer, ESO)对其进行实时估计和补偿．ADRC不需要精确的数学模型，只需利用误差反馈进行控制．但传统ADRC方法也存在一定的缺陷，例如：一般仅要求ESO渐近稳定，收敛速度有提升的空间；针对快时变干扰的估计能力不足；对干扰估计的精度有限；需要选取的参数过多，并且没有实用的参数整定方法等等．

针对传统ADRC方法存在的问题很多学者进行了一定程度的改进．Gao[2]提出了线性ADRC方法，引入“带宽”的概念，将ESO的非线性形式线性化和参数化，减少了参数数量并且赋予参数明确的物理意义，同时给出了参数的整定方法，便于实际应用．吴云洁等[3]将变结构控制的理论引入到自抗扰算法中的ESO的设计中，在保证原控制器优点的同时减少了可调参数；李大宇，邵星灵等[4-5]学者通过构造高阶ESO，获取更多的系统信息，提高了对“总和扰动”的观测精度．邱搏博，齐乃明等[6-7]通过重新构造ESO和非线性误差反馈中的非线性函数，避免了在传统ADRC中非光滑函数易引起高频颤振现象的发生．

Levant等[8-9]提出的高阶滑模观测器吸纳了滑模变结构鲁棒性强、精度高、有限时间收敛等特点，对高频干扰具有很好的观测效果，同时设计满足分离原理的条件．为有效提高ADRC对系统外部扰动和内部参数不确定等因素的适应能力，本文中引入高阶滑模观测器，替代ESO对系统所受“总和扰动”进行观测，提高扰动估计精度．

1 ADRC基本原理

ADRC是在经典PID控制技术的基础上，利用现代控制理论，运用计算机仿真实验结果归纳和综合中探索出来的，是不依赖于被控对象精确模型的、能够替代PID控制技术的、新型的实用数字控制技术[10]．ADRC由跟踪微分器(tracking differentiator, TD)、ESO和非线性状态误差反馈律(nonlinear state error feedback, NLSEF)三部分构成．

设有未知外扰作用的不确定单输入单输出受控对象：

(1)

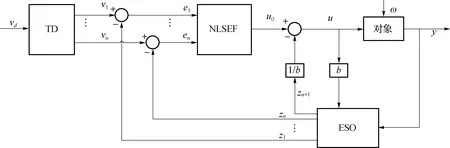
图1 ADRC结构图Fig.1 The structure of ADRC

ADRC利用TD为指令输入安排过渡过程，得到柔化后的输入信号，提高控制器的鲁棒性，并提取其微分信号；利用ESO不仅能估计出系统的状态量，还能实时估计由于模型不确定引起的内部扰动和环境引起的外部扰动等构成的“总和扰动”；应用NLSEF将TD的输出与系统状态估计值之间的误差通过非线性组合构成初始的控制量；加入对ESO估计出的“总和扰动”的补偿，得到最终的控制量．

ESO是整个ADRC方法的核心，作为一个动态过程，它只用了原对象的“输入—输出”信息，没有用到描述对象传递关系的函数的其他信息，其结构如图2所示．

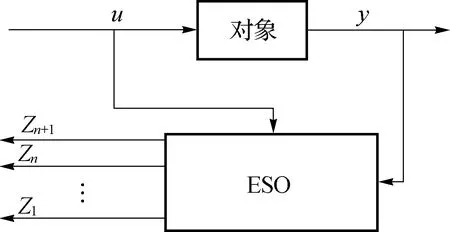
图2 ESO结构图Fig.2 The structure of ESO

当系统存在不确定性和外部扰动时，通过ESO能够将“总和扰动”的实时值估计出来，并在后续控制中给予补偿．也正是因为ESO可以实现“模型和未知外扰补偿”，使得其在不确定受控对象控制器设计中得到广泛应用．但是传统ESO为李雅普诺夫意义下的渐近稳定，收敛速度无法保证，尤其在应对快时变干扰时不能快速地实现状态和误差的估计．因此在应对诸如飞行器等需要快速抵消扰动的系统时，不能满足系统快速反应的要求．

2 ADRC技术的改进

针对传统ADRC中ESO渐近稳定、收敛速度不能保证的缺点，本文中引入鲁棒性更强、精度更高、跟踪速度更快的高阶滑模观测器代替ESO对ADRC进行改进．

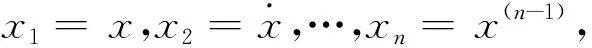
(2)

假定系统输出值y和控制输入u实时可测，未知总和扰动项f(x1,x2,…，xn,ω(t))利普希茨连续，且其利普希茨常数L>0已知，则高阶滑模观测器形式如下[11]：

(3)

引理1[11]若高阶滑模观测器的参数λi取适当值且系统输出信号y(t)和输入信号u(t)有界并且是勒贝格可测的，则在不存在测量噪声的情况下，在有限时间内，如下等式成立：

(4)

注1参数λi可以采用递归的方法来选取，若n=k时选定参数λ1,…,λk，则当n=k+1时可用作λ2,…,λk+1，即仅需设计选取新的λ1.文献[8]中提供了一组经仿真验证有效的λi,(i=1,2，…,6)的参考取值：λ1=8，λ2=5，λ3=3，λ4=2，λ5=1.5，λ6=1.1.

引理2[11]若输出信号y(t)和输入信号u(t)带有有界勒贝格可测噪声，两者所受到的勒贝格可测噪声范围为：[-ε,ε]和[-kε(n-1)/n,kε(n-1)/n],k>0，则在有限时间内，如下不等式成立：

(5)

其中正常数μi唯一取决于k和观测器参数λi.

高阶滑模观测器基于精确鲁棒微分器设计，在初始误差较小的情况下，能够保证有限时间收敛性和自动提供最优的渐近精度[12]．

引入高阶滑模观测器对ADRC进行改进，即将传统ESO对系统内部状态和“总和扰动”的观测作用，利用收敛速度更快且精度更高的高阶滑模观测器代替，进一步提高控制器对“总和扰动”的估计精度和跟踪速度．引入高阶滑模观测器改进后的ADRC结构图如图3．

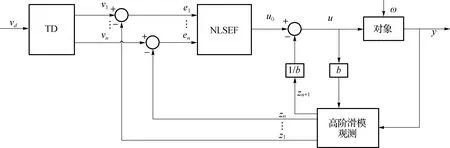
图3 改进后的ADRC结构图Fig.3 The structure of the improved ADRC

3 改进的ADRC在四旋翼飞行器控制上的应用

在四旋翼飞行器姿态小角度变化的情况下，忽略机体坐标系下三轴角速度与欧拉角速率的差异；忽略旋翼重心至机体重心的垂直距离；忽略风的干扰，不计空气摩擦；假设飞行器质量分布均匀，重心位于机体几何中心．记在地面坐标系下四旋翼飞行器中心相对原点的坐标为[x,y,z]，欧拉角为[φ,θ,ψ]，则根据牛顿-欧拉方程可得系统的数学模型为[13-14]：

(6)

式中，m为飞行器质量，g为重力加速度，l为旋翼重心到机体重心的距离，[Jx,Jy,Jz]为飞行器绕3个机体轴的转动惯量，jr为电机和旋翼的转动惯量，U1～U4分别为高度通道、滚转通道、俯仰通道、偏航通道的控制输入，其值分别为：

(7)

式中，Ωi(i=1,2,3,4)为各旋翼转速，b为旋翼升力系数，d为反扭矩系数.

从上述模型中可以看出，四旋翼滚转、俯仰和偏航3个姿态通道以及高度通道之间相互耦合，本文中通过引入估计鲁棒性更强且具有有限时间稳定性的高阶滑模观测器对系统各状态和“总和扰动”进行估计，并对“总和扰动”进行补偿．进而每个控制通道由原来的非线性、不确定对象变为积分串联型线性系统，实现了各通道的解耦控制，将系统分为4个独立的控制通道：高度通道、俯仰通道、滚转通道和偏航通道，系统结构图如图4所示．

图4 基于ADRC的控制系统结构Fig.4 The structure of control system based on ADRC

为便于阐述控制策略，将四旋翼姿态系统模型写成与ADRC理论相对应的形式：

(8)

式中fi(·)(i=1,2,3,4)为各通道所受“总和扰动”，为内部扰动．

ADRC以及高阶滑模观测器的设计完全满足分离性原理，即四旋翼姿态控制系统可以每个控制通道分别独立设计TD、高阶滑模观测器和NLSEF．下面以俯仰通道为例，给出俯仰通道完整控制算法．

被控对象

(9)

1) TD安排过渡过程

(10)

式中：θd为俯仰通道指令输入，θd1为指令输入跟踪信号，θd2为θd1的微分信号，r为速度因子，h为积分步长，以及最速控制综合函数：

(11)

2) 高阶滑模观测器估计状态和“总和扰动”

(12)

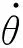
3) 扰动补偿与控制量形成

(13)

其中

(14)

高度通道、滚转通道以及偏航通道控制器设计与俯仰通道类似．

4 数值仿真及结果分析

四旋翼飞行器仿真模型采用式(6)，考虑数学模型、ADRC部件以及高阶滑模观测器运算较为复杂，本文中采用S-函数编辑各重要模块，基于MATLAB/Simulink模块建立系统仿真模型，仿真采样周期取h=0.01 s． 本文中选取的四旋翼飞行器仿真参数和控制器参数见表1和2．

表1 四旋翼飞行器仿真参数

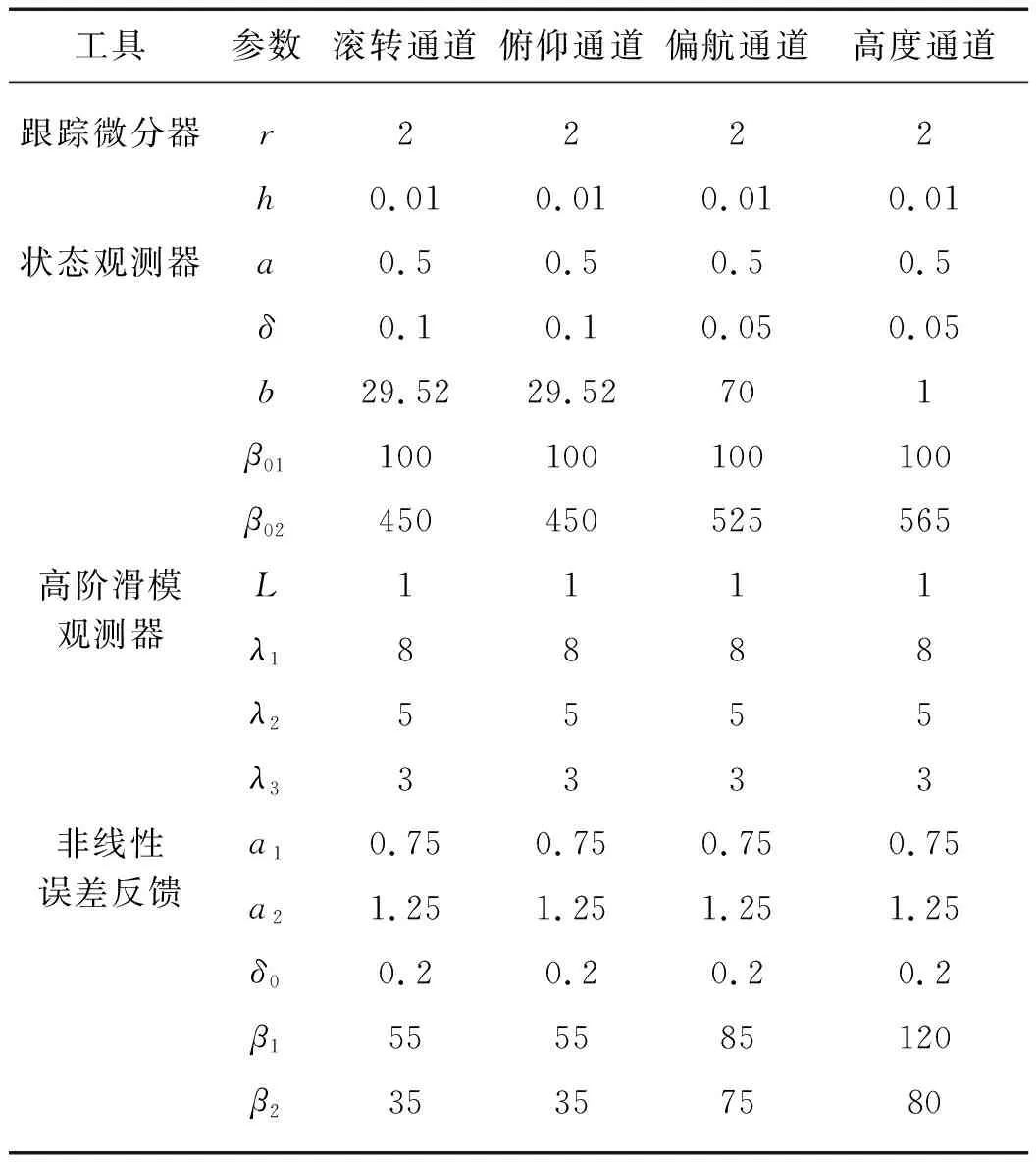
表2 控制器设计参数

1) 姿态角跟踪实验

假设四旋翼飞行器三个姿态角初始值分别为φ0=5°，θ0=5°，ψ0=10°，初始高度为0 m，在初始时刻给出目标指令φd=30°，θd=10°，ψd=15°，控制飞行器在2 m高度实现姿态稳定．为体现引入高阶滑模观测器改进后的ADRC相对传统ADRC的控制效果差异，仿真过程加入了与传统ADRC控制器控制效果的对比．仿真效果如图5所示．

从图5可以看出引入高阶滑模观测器改进传统自抗扰方法所设计的控制器的姿态角以及高度跟踪响应曲线能够很好地跟踪给定期望信号．在TD安排的过渡过程完全相同的情况下，相比传统ADRC，改进后的控制器能够以稍快的速度跟踪给定信号．由于TD的柔化作用，指令信号经安排过渡过程后均由“0”值光滑过渡到给定值，这也是仿真开始阶段角度有归“0”走势的原因．当3个姿态角同时发生变化时，由于四旋翼姿态角通道之间的强耦合，3个通道之间会有相互的影响，通过引入高阶滑模观测器将这些影响视为系统内部扰动并实时观测补偿，使得姿态角通道之间的相互影响得以消除．

图6给出定高2 m姿态角跟踪过程中的控制力变化曲线，改进前后两种控制器产生的控制力差别不大，均能保证飞行器以较高的精度飞行．这表明，当不考虑外部扰动时，两类ADRC均能及时估计并补偿系统参数摄动所引起的“总和扰动”．

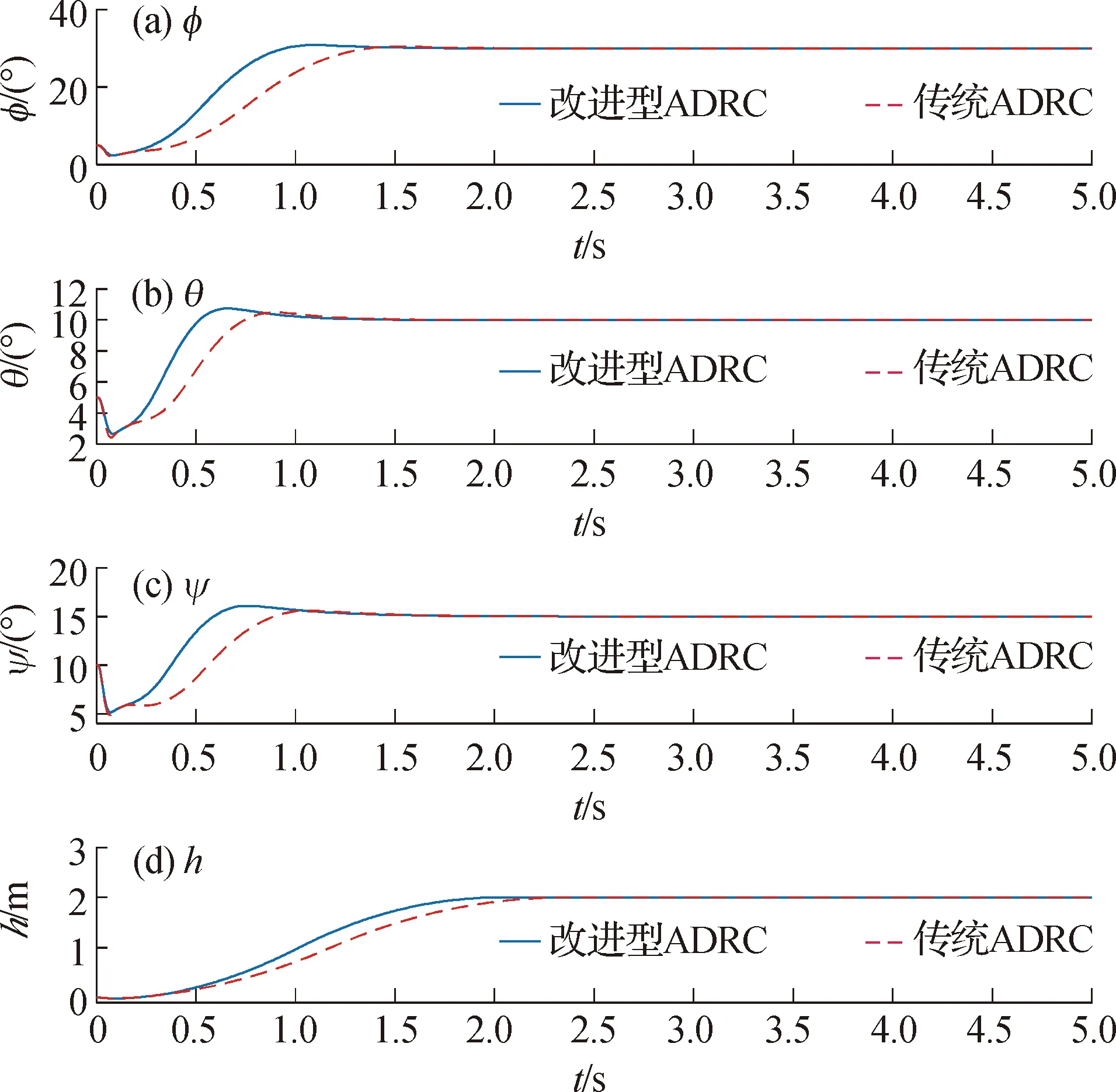
图5 姿态角跟踪实验姿态角和高度响应曲线Fig.5 Attitude angle and height response curves in the attitude angle tracking experiment

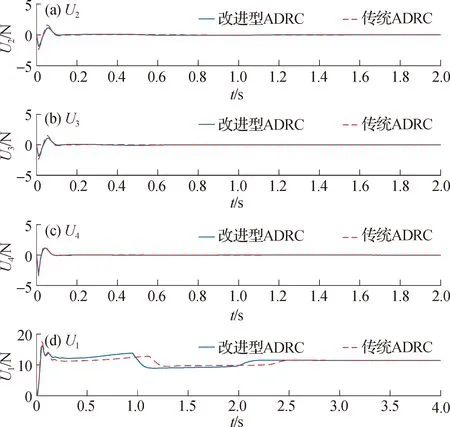
图6 姿态角跟踪实验控制力曲线Fig.6 Control force curves of attitude angle tracking experiment

2) 抗扰性能测试

定高姿态角跟踪实验仅仅体现出了改进后的ADRC相对传统ADRC具有更快的响应速度，并未体现出较大的改进效果．为验证改进后的控制器的抗干扰能力的提升效果，在四旋翼定点悬停状态下，分别在3个姿态角通道中加入高斯白噪声来模拟传感器噪声，同时考虑姿态角受到外部突发干扰的情况，在2～6 s内加入幅值为0.05 N·m，频率为1 Hz的方波信号来模拟阵风干扰，外部扰动信号如图7所示．

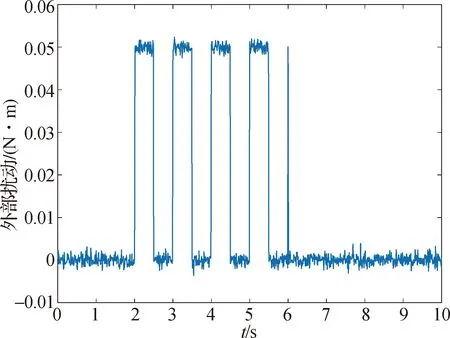
图7 外部扰动信号Fig.7 Curve of the external disturbance

在此干扰信号作用下四旋翼姿态输出曲线如图8所示．

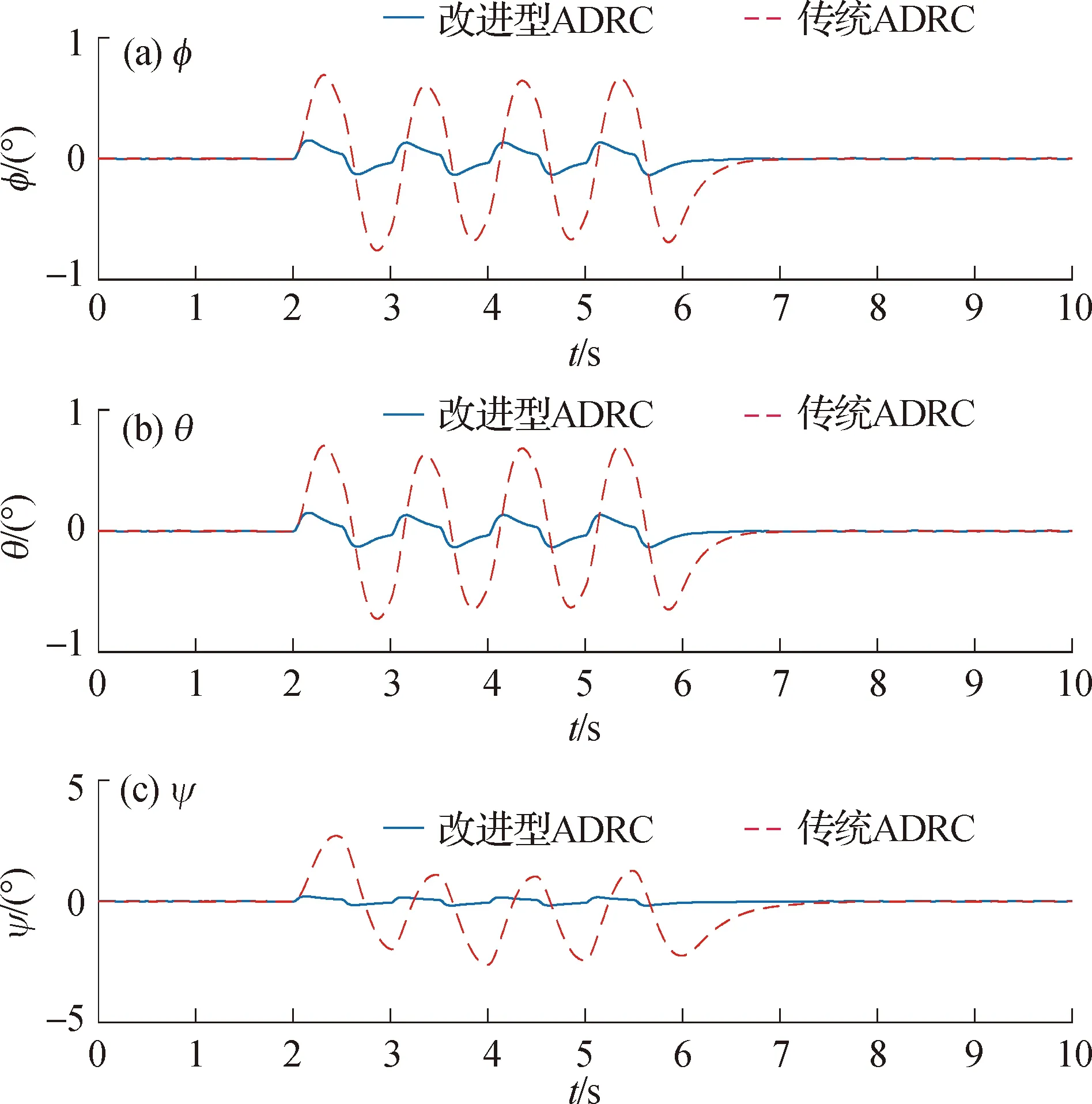
图8 抗扰能力实验响应曲线Fig.8 Response curves of disturbance resistance test

由图7和8可以看出，在存在外部扰动的情况下，引入高阶滑模观测器改进后的ADRC和传统的ADRC都能够在一定程度上抑制扰动．但在应对快变扰动时，引入高级滑模观测器改进的ADRC展现出了更强的鲁棒性能．

仿真过程中传统ESO与高阶滑模观测器对“总和扰动”的估计效果对比如图9所示．

图9 高阶滑模观测器与ESO估计“总和扰动”效果对比Fig.9 Estimation of "total disturbance" by high order sliding mode observer and extended state observer

由图9可知，在相同外部扰动信号的作用下，高阶滑模观测器相比传统ESO能够更快更精确地跟踪各通道的“总和扰动”，因此改进后的ADRC相比传统ADRC表现出来更好的控制效果，而这归根结底是因为高阶滑模观测器的有限时间稳定特点，使其在应对快时变扰动时具有更快的跟踪速率．

抗扰能力实验控制力曲线对比如图10所示．

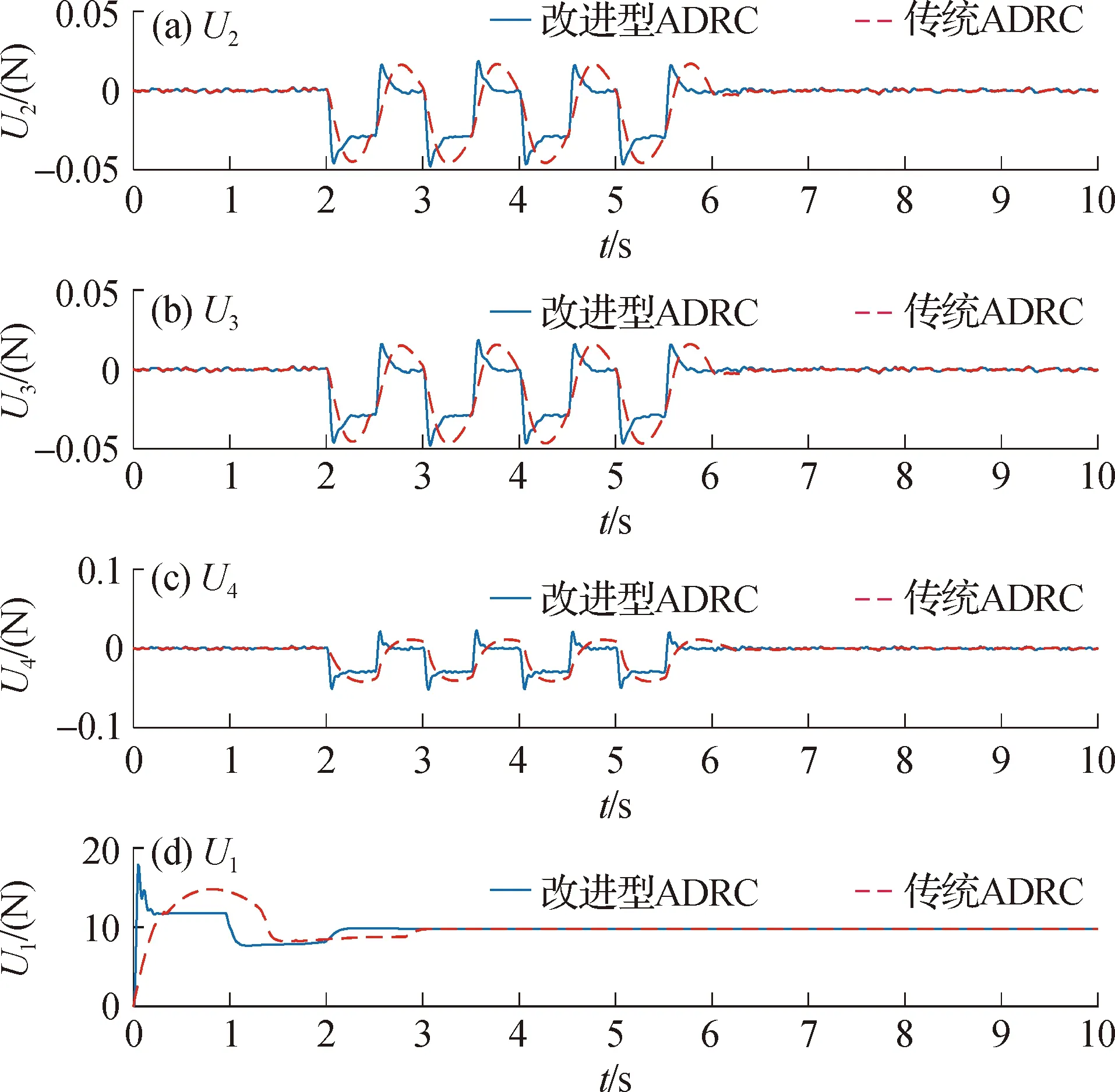
图10 抗扰能力实验控制力曲线Fig.10Control force curve of disturbance resistance test

由图10可以看出，当四旋翼姿态控制系统受到外部干扰作用时，改进后的ADRC相比传统ADRC能够产生更加稳定有效的控制力，这也同样是因为高阶滑模观测器有限时间稳定的优点，使其对快变扰动较传统ESO更为敏感，从而使得控制器反应更迅速．

5 结 论

本文中引入高阶滑模观测器代替传统自抗扰算法中的ESO对自抗扰算法进行了改进，提高了传统自抗扰算法对扰动的估计速度和精度．基于四旋翼飞行器针对该飞行器非线性、强耦合、对外部干扰敏感等特点，应用引入高阶滑模观测器改进后的自抗扰算法设计了姿态控制系统，通过仿真验证表明应用改进后的ADRC所设计的四旋翼姿态控制系统具有良好的跟踪性能、抗干扰能力和鲁棒性能．