带关闭期的随机N-策略的 M/G/1 排队模型的适定性
2018-10-09艾合买提阿不来提
艾合买提·阿不来提,张 文
(1. 新疆财经大学应用数学学院,新疆乌鲁木齐830012;2. 厦门大学数学科学学院,福建厦门361005)
1 预备知识
众所周知,近年来许多学者对随机N-策略下的排队系统进行了深入的研究(见文献[1-14]和其中引用的参考文献). Yadin等[1]首次考虑了随机N-策略下的排队系统.之后很多学者广泛地推广了这类系统.例如,Kella[2]研究了带假期的N-策略M/G/1排队系统.Borthakur等[3]将带有指数性启动时间的M/M/1排队模型[4]推广到了带有一般启动时间的情况.Lee等[5]研究了带单休假和多个假期的批量到达的N-策略M/G/1排队系统.1991年Takagi[6]给出了关闭期的概念,有很多学者对这类排队模型进行了研究.Ke[7]给出了一类具有故障、启动及关闭期的M/G/1排队系统并对其进行了研究.Liu等[8]讨论了带启动和关闭期的N-策略下的两种不同类型的M/G/1 排队系统.具有随机N-策略的M/G/1排队模型也被许多作者进行了研究[9-10].Feng等[9]通过向量马尔科夫过程的方法研究了带关闭期的随机N-策略和休假策略的M/G/1排队模型并且得到了该系统处于稳态的充分必要条件.
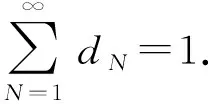
本文中在以下假设下讨论该排队模型:
1) 顾客到达时间间隔τn是相互独立且服从同分布,服从于参数为λ-1(λ>0) 的负指数分布,即
P{τn≤t}=1-e-λt,n=1,2,….
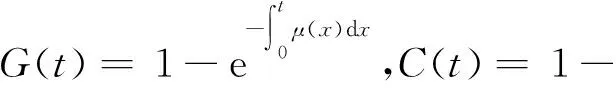
3) 以上都是相互独立的随机变量.
4) 顾客进入系统后要等到服务开始.
5) 服务基于先到先服务的规则进行,系统有无限的排队空间.
本文中根据 Hille-Yosida 定理,Phillips 定理与 Fattorini 定理,证明具有多个工作休假和休假中断的M/G/1 排队系统存在唯一非负的满足概率条件的时间依赖解.
根据文献[9],该模型可表示如下:
(1)
λpi-1(t,x),i≥2,
(2)
j=1,2,…,i-1,
(3)
i=1,2,…,
(4)
(5)
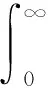
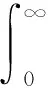
(6)
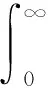
i=2,3,…,
(7)
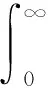
(8)
κi0(0)=di,pi(0,x)=0,i=1,2,…,
q(0,x)=0.
(9)
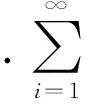
μ(x)≥0,

ω(u)≥0,

交通强度为
为了方便,引入以下符号:
Γ3=(λ,0,0,…)T,
Γ4=(μ(x),0,0,…).
取状态空间X如下:
X={(p,κ,q)|p∈X1,κ∈Z,q∈L1[0,∞),
‖(p,κ,q)‖=‖p‖X1+|κ|+‖q‖L1[0,∞)},
其中:
X1={p∈L1[0,∞)×L1[0,∞)×…|‖p‖=
显然,X是一个Banach空间.令
pn(x),q(u)均是绝对连续函数,且
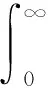
对∀(p,κ,q)∈D(A),定义算子A为

如果对 ∀(p,κ,q)∈X定义算子B为如下:
Bq=0,
D(B)=X,
则该模型即方程组(1)~(9) 可转化成 Banach 空间X中的抽象 Cauchy 问题,即
(d1,d2,0,d3,0,0,d4,0,0,0,…),
(10)
(p,κ,q)(0)=((0,0,…),(d1,d2,0,…,
(11)
本文中始终假定
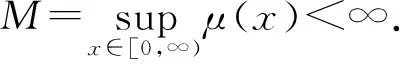
2 主要结果
定理1算子A生成正C0-半群T(t).

i=1,2,…,
(12)
(γ+λ)κi0=πi0,i=1,2,…,
(13)
(γ+λ)κij=λκi,j-1+πij,i=2,3,…,
j=1,2,…,i-1,
(14)
(15)

(16)
i=2,3,…,
(17)
(18)
由式(12)和(15)有
(19)
(20)
由式(19)~(20)以及式(16)~(18)得
a1=p1(0)=
(21)
ai=pi(0)=
λκi,i-1,i≥2,
(22)
b=q(0)=
(23)
将式(23)带入(21)得
(24)
如果应用Fubini定理并且记
(25)
则式(24)和(22)可改写成如下
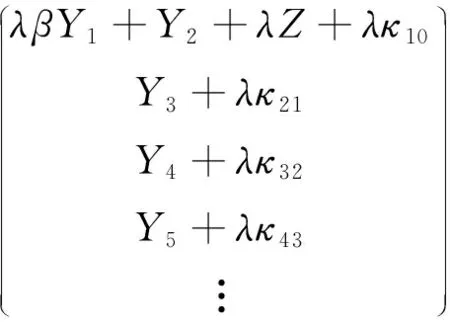
⟹
(26)
(27)
再由式 (23)得
(28)
这样结合式(19),(20)以及式(25)~(28)得到
‖(p,κ,q)‖= ‖p‖Y+|κ|+‖q‖L1[0,∞)=
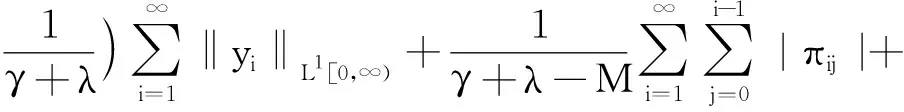
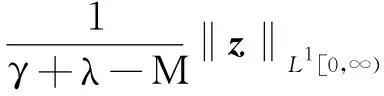
(29)
式(29)表示(γI-A)-1存在并且当γ+λ>M时
(30)
下面证明D(A) 在X中稠密.
令
L=
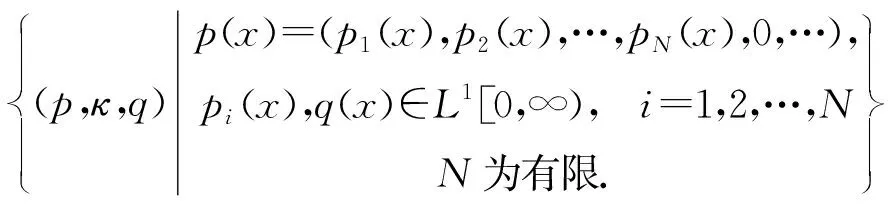
显然,L在X中稠密的. 如果再令
W={p,κ,q)|p(x)=(p1(x),p2(x),…,pm(x),
0,…),

根据文献[11]直接可以证明W在X中稠密. 因此只需要证明D(A) 在W中稠密即可.
取 (p,κ,q)∈W,则存在ci>0,c0>0 使得pi(x)=0,x∈[0,ci],q(x)=0,x∈[0,c0],i=1,2,…,m. 从而有
pi(x)=0,q(x)=0,x∈[0,2s],
这里
0<2s 令 其中 i=1,2,…,m, 说明D(A) 在W中稠密,换言之,D(A) 在X中稠密. 由以上的结果以及 Hille-Yasida 定理[12]可知A生成一个C0-半群. 易知 B:X→X, ‖B‖≤λ+1 (31) 是有界线性算子,因此根据C0-半群的扰动定理[13]可推出A+B生成C0-半群T(t). 由式(13),(14),(19),(20)知道.如果 (y,π,z) 是正向量则 (p,κ,q) 也是正向量. 因而,(γI-A)-1是正算子. 显然,B也是正算子. 注意到 (γI-A-B)-1= [I-(γI-A)-1B]-1(γI-A)-1. (32) 根据式(30)容易可知,当 γ>M+1 时有 ‖(γI-A)-1B‖<1, 即 [I-(γI-A)-1B]-1存在且有界,且 (33) 因此 [I-(γI-A)-1B]-1也是正算子. 进而,由式(32) 和 (33) 知 (γI-A-B)-1是正算子. 最后根据文献 [14],推出 因此T(t) 也是正的. 证毕. 定理2系统 (1)~(9) 存在唯一的非负解. 证毕. 本文中主要对带关闭期的随机N-策略的M/G/1 排队系统进行了分析与研究. 主要工作是应用算子理论、 Hille-Yosida定理、Phillips 定理以及 Fattorini 定理证明了 该模型存在唯一的非负解并且满足概率条件. 本文中考虑了该模型时间依赖解方面的问题,据我们所知,至今该模型还没有其他结果. 因此该模型值得进一步研究,例如,该模型时间依赖解的渐进行为等. 这是我们下一个要讨论的话题.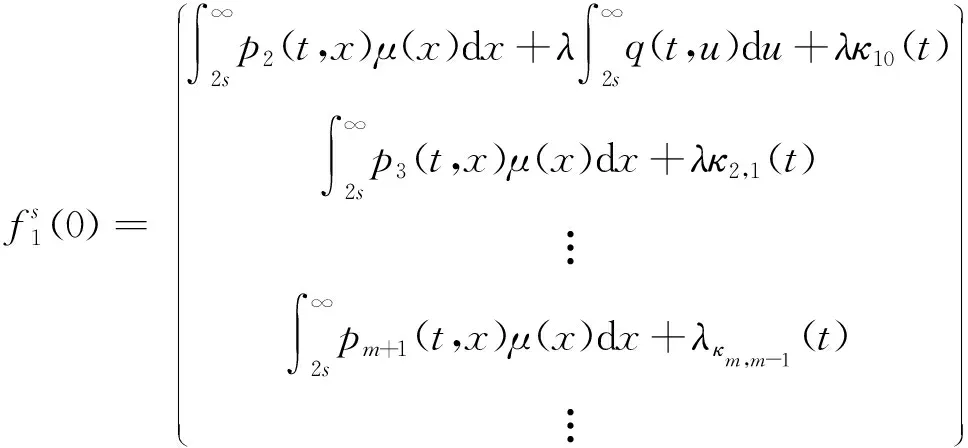
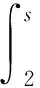
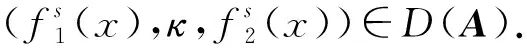
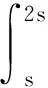
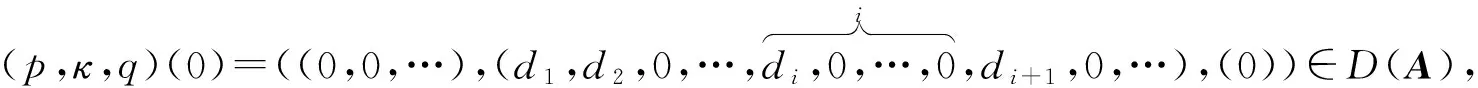
3 结 论
