局部(弱)紧性的理想收敛刻画

王 波,施慧华,孟庆丰

(华侨大学数学科学学院,福建泉州362021)

1 预备知识

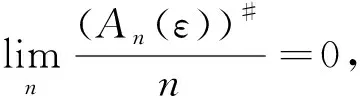
本文中的主要工作是把理想收敛这一工具应用到Banach空间的研究中，利用序列的(弱)极大理想的收敛性来刻画集合的局部(弱)紧性等.

现将常见符号约定如下：N表示自然数集，R表示实数集，X为Banach空间，B(x0,r)表示闭球(即B(x0,r)={x:‖x-x0‖≤r})，Bo(x0,r)表示开球.特别地，B(0,1)=BX为X的单位球.

定义1对自然数集N，称⊂2N为N的一个理想，如果满足：

(i) 如果D⊂E且E∈，则D∈(遗传性)；

(ii) 如果D,E∈，则D∪E∈(有限并运算的封闭性).

定义2对Banach空间X中的序列|xn}及x∈X，记

A(ε)={n∈N:‖xn-x‖≥ε}, ∀ε>0.

(i) 称{xn}-收敛于x(或xnx),若任意的ε>0，有A(ε)∈;

(ii) 称{xn}w--收敛于x，若每个x*∈X*，有{x*(xn)}-收敛于x*(x).

定义3称Banach空间X中的集合C是局部紧集(相应地，局部弱紧集)，如果对任意的c∈C，都存在δ>0，使得C∩{x∈X:‖x-c‖≤δ}是紧集(相应地，弱紧集).

引理1[15]设X是Banach空间，C⊂X是非空闭凸集，则以下结论等价：

(i)C是局部紧集(相应地，局部弱紧集)；

(ii)C∩rBX是紧集(相应地，弱紧集)，对任意的r>0;

(iii)C∩B(x0,r0)是紧集(相应地，弱紧集)，对某个x0∈C及r0>0;

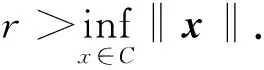
引理2(James定理) 设B为Banach空间X中的有界弱闭集，则B是弱紧当且仅当每个x*∈X*在B上达到其上确界.

2 主要定理及其证明

定理1设是非平凡极大的可容理想，X是Banach空间，非空闭凸集C⊂X.则C是局部紧⟺对任意有界序列{xn}⊂C，{xn}-收敛于C中的元．

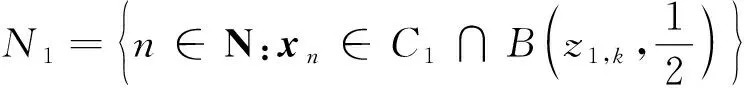
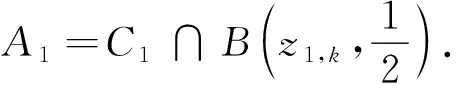
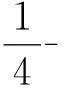
因N1∉，故存在某k∈N使得

归纳地,可得一列递减的紧集序列{Ak}，满足diam(Ak)≤21-k，同时得到N的子集序列{Nk}，有

Nk∉, ∀k∈N.

实际上,对任意的ε>0，取充分大的k，使得Ak⊂Bo(x,ε)，即

Nk⊂{n∈N:‖xn-x‖<ε}.

由Nk∉，可得{n∈N:‖xn-x‖<ε}∉.由理想的极大性知

{n∈N:‖xn-x‖≥ε}∈.

推论1设是非平凡极大的可容理想，则Banach空间的非空子集C是紧集⟺对任意序列{xn}⊂C，{xn}-收敛于C中的元.

证明证明方法类似定理1.

推论2设是非平凡极大的可容理想，则Banach空间的非空子集C是相对紧⟺对任意序列{xn}⊂C，有{xn}-收敛.

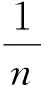
‖yn-x‖≤‖yn-xn‖+‖xn-x‖≤

因此

{n∈N:‖xn-x‖<ε}⊂{1,2,…,n0}∪{n∈

N:‖yn-x‖<2ε}.

故可得

{1, 2,…,n0}∪{n∈N:‖yn-x‖<2ε}∈

{n∈N:n>n0}∩({1,2,…,n0}∪{n∈N:

‖yn-x‖<2ε})={n>n0:‖yn-x‖<2ε}∈

进一步

即

{n∈N:‖yn-x‖≥2ε}∈.

从而

定理2设是非平凡极大的可容理想，X是Banach空间，C⊂X是非空闭凸集，则C是局部弱紧⟺C中任意有界序列{xn}都w--收敛于C中的元.

证明充分性.任取r>0，记C1=C∩rBX，则C1是有界闭凸集.因此每个

且存在{xn}⊂C1，使得

由假设知,{xn}w--收敛于x∈C1.因此

则存在{xn}的子列{xnk}，使得

〈x*,xnk〉→〈x*,x〉，

即

由James定理可得C1为弱紧集，故C是局部弱紧.

必要性.设任意有界序列{xn}⊂C，则存在r>0，使得{xn}⊂C∩rBX.结合引理1知C1≡C∩rBX是弱紧集.对任意的x*∈X*，{〈x*,xn〉}有界.则由推论1知存在.令

T(x*)=-lim〈x*,xn〉， ∀x*∈X*.

下证T∈X**.设x*,y*∈X*及数a,b∈R，则

T(ax*+by*)=-lim〈ax*+by*,xn〉=

a(-lim〈x*,xn〉)+b(-lim〈y*,xn〉)=

aT(x*)+bT(y*),

所以T是X*上的线性泛函.此外，记

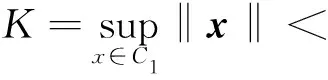
则对任意的n∈N，任意的x*∈X*，

|〈x*,xn〉|≤K‖x*‖.

因此

T(x*)≤K‖x*‖，

从而

T∈X**.

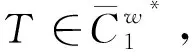
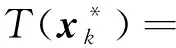
有

∀k=1,2,…,m.

则

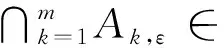
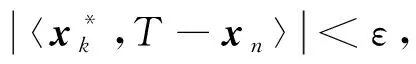
即

由T的定义，可得

w--limxn=T，

定理得证.

推论3设理想是非平凡极大的可容理想，则Banach空间X的非空有界弱闭子集C是弱紧⟺C中的任意序列{xn}都w--收敛于C中的元.

推论4设理想是非平凡极大的可容理想，则Banach空间X是自反空间⟺X中每个有界序列都w--收敛.