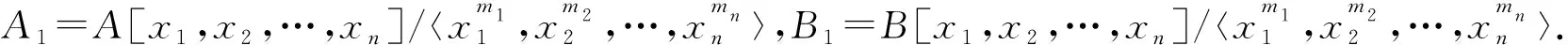对偶数环导出范畴的Recollements

刘宏锦，陈清华

(1. 龙岩学院信息工程学院，福建龙岩364012;2. 福建师范大学数学与计算机科学学院，福建福州350117)

设R是环，R的对偶数环R[ε]是R的一元多项式环的商环R[x]/〈x2〉.对偶数环R[ε]上的模是微分R-模(M，ε)，其中M是R-模，ε是模M上平方为零的自同态.如果(M，ε)，(M′，ε′)都是微分R-模，两者之间的态射f:(M,ε)→(M′,ε′)是R-模态射f:M→M′，则满足fε=ε′f.对于R[ε]上的模的研究最早出现在文献[1]中.Ringel等[2]研究了路代数kQ上由完备微分模构成的Frobenius范畴的稳定范畴与kQ上导出范畴的根范畴之间的关系.Wei[3]和Xu等[4]考虑了微分模的Gorenstein同调理论.

导出范畴的recollements起源于Grothendieck关于代数几何中层的相关函子的考察.1982年，Beilinson等[5]给出了三角范畴recollements公理化定义.最近，刘宏锦等[6]考虑了在导出范畴recollements下，广义AR猜想的保持性问题.由已知的recollements构造新的recollements是一个有趣的问题，如文献[7-11]等.注意到这些结果都是利用Koenig定理将已有代数的导出范畴的recollements提升到新代数的导出范畴的recollements.本文中利用Koenig定理考虑环的导出范畴的recollements在对偶数环上的提升，证明了若环A的上有界导出范畴D-(A)允许有关于环A1和A2的上有界导出范畴D-(A1)和D-(A2)的recollement，则A的对偶数环A[ε]的上有界导出范畴D-(A[ε])允许有关于D-(A1[ε])和D-(A2[ε])的recollement.

1 预备知识

本文涉及到的环A都具有单位元，考虑的模都是右A-模.右A-模范畴记为A-Mod，本文中用A-Proj表示所有投射模构成的范畴；A-proj表示所有有限生成投射模构成的范畴；D-(A)，Db(A)分别表示A-Mod 上的上有界复形，有界复形的导出范畴；Kb(A-Proj)，Kb(A-proj)分别表示A-Proj，A-proj上的有界复形的同伦范畴.

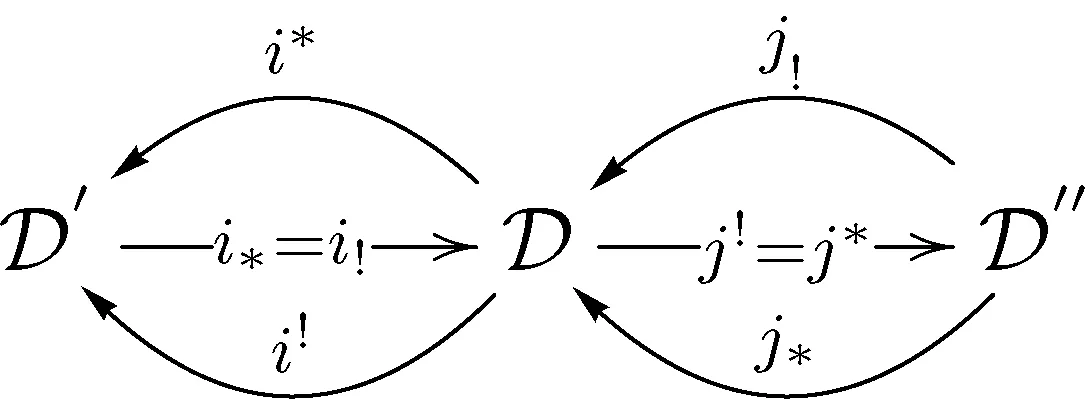
是指三角范畴的6个正合函子：

i*=i!:′→;i*,i!:→′；

j*=j!:→″;j*,j!:D″→D;

满足如下4个条件：

(i) (i*,i*),(i!,i!),(j!,j!)和(j*,j*)均是伴随对；

(ii)i*,j!和j*均是满嵌入函子；

(iii)j*i*=0;

i!i!X→X→j*j!X→i!i!X[1],

j!j!X→X→i*i*X→j!j!X[1].

定义2[12]设A是环，T·∈Kb(A-Proj).称T·是偏倾斜复形，如果T·满足以下条件：

(i) 对任意i≠0，有HomKb(A-Proj)(T·，T·[i])=0；

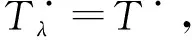
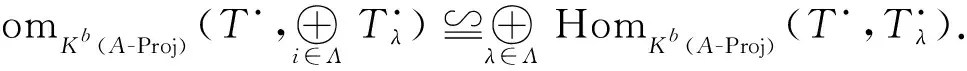
注Kb(A-proj)上的复形X·称为完备复形，也称为紧对象，根据文献[12]，HomKb(A-proj)(X·，-)与任意直和可交换.因此，完备复形X·只要满足定义2(i)，则X·是偏倾斜复形.

定理1[12-13]设A,A1和A2是环，则有上有界导出范畴的recollement

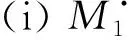
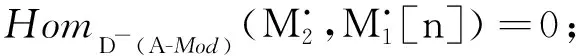
2 主要结果及应用

本文中的主要结论是

定理2设A，A1和A2是环.如果A的上有界导出范畴D-(A)允许有一个关于A1，A2的上有界导出范畴D-(A1)，D-(A2)的recollement，则A的对偶数环A[ε]的上有界导出范畴D-(A[ε])允许有如下的recollement

在证明定理2之前，需要如下引理.

引理1设X是A-模，则EndA[ε](X⊗AA[ε])中的态射均具有下三角

的形式，其中α,β∈EndA(X).

证明右A[ε]模X⊗AA[ε]同构于A上的微分模

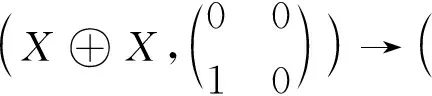
的形式，其中ai∈EndA(X),i=1,2,3,4,且满足

故a2=0,a1=a4.

定理2的证明事实上，对偶数环A[ε]中的元素可表示为二元数组(a1,a2)，其中a1,a2∈A.作为加群A[ε]=A⊕A，其乘法定义如下

(a1,a2)·(b1,b2)=(a1b1,a2b1+b2a1).

因此，A的单位元也可视为A[ε]的单位元，作为A-A-双模A[ε]≌A⊕A.

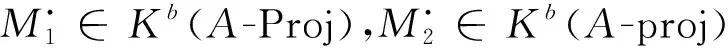
(i) 作为加群，有如下同构

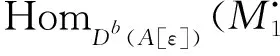
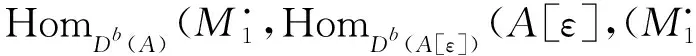
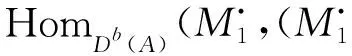
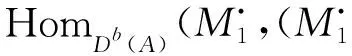
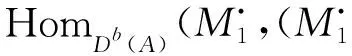
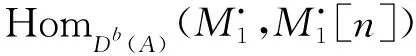
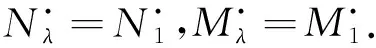
所以

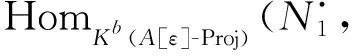
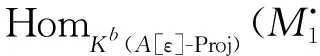
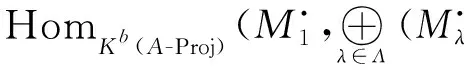
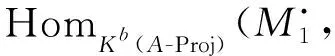
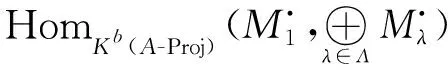
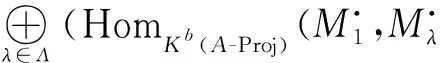
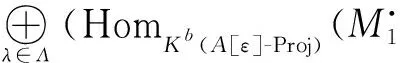
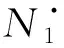
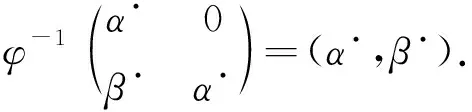
(iii) 对任意n∈Z，有

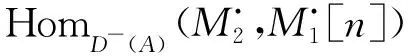
0.

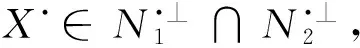
因为

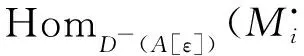
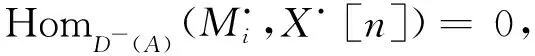
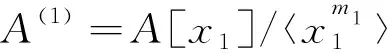
作为R-R-双模有同构

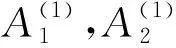
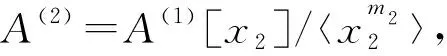
推论1设A，A1和A2是环.如果A的上有界导出范畴D-(A)允许有一个关于A1，A2的上有界导出范畴D-(A1)，D-(A2)的recollement.对任意正整数n,m1,m2,…,mn，令

则A(n)的上有界导出范畴D-(A(n))允许有如下的recollement

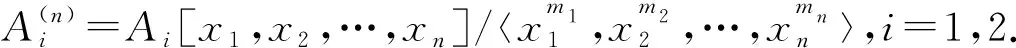
定义3设A,B均是环.如果Db(A)和Db(B)作为三角范畴等价，则称A与B导出等价.

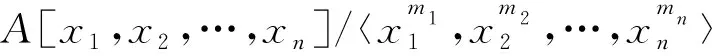
证明根据Rickard定理(参见文献[14]，定理6.4)，Db(A)和Db(B)作为三角范畴等价当且仅当D-(A)和D-(B)作为三角范畴等价.又因为存在平凡的recollement.

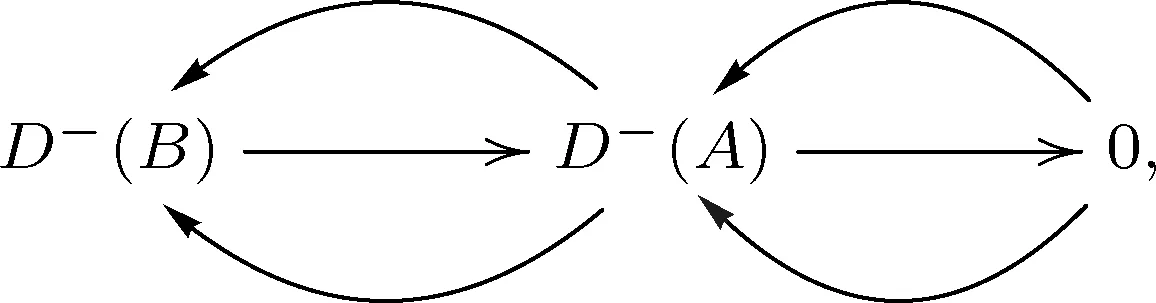
所以由推论1，存在平凡的recollement