互相关系数自约束的重力三维反演与高效求解
2018-10-09梁生贤
梁生贤
中国地质调查局成都地质调查中心,成都 610081
0 引言
重力反演就是根据观测场值求解场源的信息,是资料定量解释的重要环节之一。物性反演将模型空间离散化为若干个单元,只求解各单元相应的密度值,这种方法易于模拟复杂的地质体[1],逐渐成为重力三维反演的重要方向[2]。本文所讨论的就是物性反演。它是线性离散不适定问题,加之三维反演的数据量比待求解的模型量更少、系数矩阵(核矩阵)严重病态性和观测数据受误差影响等,多解性和不稳定性严重;因此,如何使得解模型更加符合实际情况是反演关注的主要问题之一。此外,当观测数据量很大时,系数矩阵大型稠密,反演涉及到大规模数据的存储与运算,在实际运算中须考虑到这一棘手问题。
在不适定问题求解方面,Tikhonov正则化方法是目前应用最为广泛的算法之一,它在一定意义上有效减少了解的多解性和不稳定性。已有研究表明,在正则化反演中尽可能地利用先验信息对场源施加约束,可使解模型更加符合实际情况,如:Li等[3-4]在重磁反演中通过加入深度加权函数来克服位场的“趋肤效应”;Paoletti等[5]提出位场自约束反演概念,指出位场本身包含了大量的潜在信息,利用这些潜在的信息对模型自约束可提高反演结果的可靠性;Sun等[6]利用磁场两个方向上的水平梯度数据计算互相关系数,得到空间加权函数,并将空间加权函数引入正则化反演的模型约束中,显示这种模型自约束反演结果对场源的边界刻画更清晰。
在节省计算成本方面,主要有并行计算[7-8]、核矩阵压缩、重构[9-13]以及快速正演计算[1-2,14]等方法,其中并行计算需要依靠计算机硬件设备,核矩阵压缩则会导致部分信号失真等。对于Tikhonov正则化反演,最终都归结为大型线性方程组问题的求解。Krylov子空间迭代法是求解大型线性方程组问题的一种有效途径,在位场反演中应用较多的为共轭梯度法[9-10, 15],近年来LSQR(最小二乘QR分解)算法[16]也越来越多地被应用于位场数据反演中[17-19];对于非病态线性方程组两者等效,而对于病态线性方程组后者求解更稳定。
本文从提升重力反演结果的可靠性和节省计算成本两个方面着手。其一,将快速扫描的互相关系数作为先验信息,通过处理引入到重力正则化反演的目标函数中,以提高反演结果的可靠性;其二,利用LSQR算法求解线性方程组问题,并对其进行相应的改进,与快速正演计算方法结合,以节省计算成本。最后通过理论模型和实际数据来展示上述方法的应用效果。
1 反演理论
1.1 正则化反演
重力正演公式可写为
d=Am。
(1)
式中:m为M阶模型向量;d为N阶数据向量;A为N×M阶核矩阵,其元素A(i,j)为第j个模型单元在地表i处的重力响应核函数,在反演中保持不变。
物性反演的任务是根据观测数据向量反求模型向量。由于反演是不适定的,Tikhonov正则化目标函数构制如下:
(2)
式中:Δd为观测数据向量与模型响应向量之间的残差;Δm为模型修改向量;λ为正则化因子或拉格朗日因子,体现了数据拟合与模型约束之间的某种“折衷”;D为模型约束矩阵。此外,为了克服重磁观测幅值随场源深度增加而迅速衰减的“趋肤效应”,通常加入一个深度加权函数,在仅考虑深度方向的情况下可写为[3-4]
Ddepth=diag1/(z1)β/2,1/(z2)β/2,…,
1/(zM)β/2。
式中:zj为模型单元中心埋深,j∈[1,M];β取1.5~2.0。
根据极值条件,求目标函数E(Δm,λ)关于模型修改向量Δm或ΔmT的偏导数,并令其等于0,可得模型空间迭代求解公式:
Δm=(ATA+λDTD)-1(ATΔd)。
(3)
Siripunvaraporn等[20]基于Occam反演策略提出数据空间算法,在数据量N远小于模型量M的情况下,可大幅度提高计算效率,数据空间迭代求解公式为
Δm=(DTD)-1AT[λI+A(DTD)-1AT]-1Δd。
(4)
式中,I为单位矩阵。
对于大规模重力数据三维正则化反演而言(数据量可能为几千甚至上万,模型量可能达几十万甚至百万),无论模型空间还是数据空间,直接法(奇异值分解)求解都需要耗费巨大的计算量和存储量(表1)。
1.2 利用互相关系数与深度加权的约束反演
在反演中,尽可能地利用已知地质信息(包括地表地质、钻孔以及地震资料等)对场源施加约束是提高解的可靠性有效而实用的措施,但在有些情况下,地质信息并不充足。
互相关系数[21-22]表征了实测重力异常与模型单元核函数的相关程度,其绝对值越接近1,表示该单元对重力异常的贡献可能性越大,且具有计算简单而快速的特点[23-24]。因而,可根据互相关系数的绝对值判断模型单元的重要性,从而将相对重要的模型单元作为先验信息对模型进行加权约束。并鉴于利用剩余异常计算所得的互相关系数成像结果可靠性较高[23-26],利用每步反演迭代的拟合残差计算互相关系数,取绝对值和归一化后对模型进行约束:
Dω=diag1/ω1,1/ω2,…,1/ωM。
(5)
式中:Dω为互相关系数约束矩阵;ωj为互相关系数,其数学表达式[23-24]为
(j=1,2,…,M)。
(6)
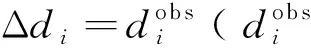
此外,相邻单元的互相关系数往往是渐变的,整体具有平缓变化的特点,因而无需再加入模型粗糙度约束矩阵。考虑到位场“趋肤效应”,令D=Dω·Ddepth。
我们根据文献[4]中的理论模型来展示不同算法的加权结果。该理论模型(图1)由两个倾斜方向相反的脉状体异常体组成[4],其中:向西倾斜的长脉状体剩余密度为1.0 g/cm3,向东倾斜的短脉状体剩余密度为0.8 g/cm3。正演数据密度:东西方向点距50 m,南北方向点距100 m,共861个数据。将数据加入4%的随机噪声,模型水平方向剖分与数据网格一一对应,垂向剖分24层,共20 664个模型单元。
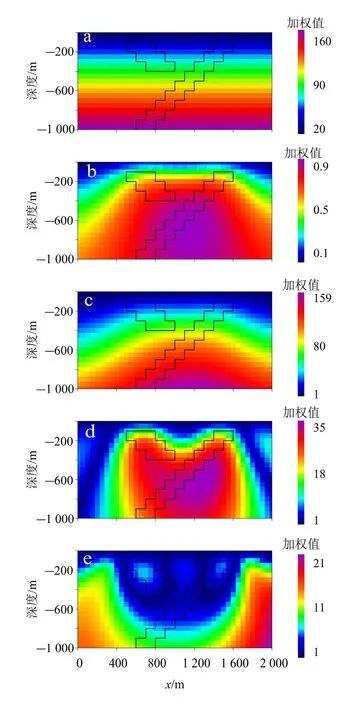
图2为理论模型计算的单元权重结果。由图2可见:仅利用深度加权时(图2a),水平向各单元权重相同,加权值仅在垂向随深度增加而变大;仅利用互相关系数加权时(图2b),模型单元权重依赖于互相关系数,而互相关系数对场源的准确位置反映较差,求解结果可能会出现偏差;同时利用深度与互相关系数加权时(图2c、d、e),由于一般情况下深度加权值的量级远大于互相关系数的量级,因而不至让反演结果过分地依赖于互相关系数,模型迭代求解从深部开始(图2c),随着迭代进行,拟合残差逐渐变小,根据拟合残差计算所得的互相关系数逐渐趋于0附近,各单元权重对深度加权的依赖减小,相应的加权值也总体变小,其形态逐渐逼近理论模型(图2d、e)。可见,同时利用互相关系数与深度加权的模型约束无疑使得先验信息更加丰富,其本质上属于自约束反演[5]的一种,有助于提高反演结果的可靠性。

表1 模型空间、数据空间与分块矩阵LSQR方法计算成本对比
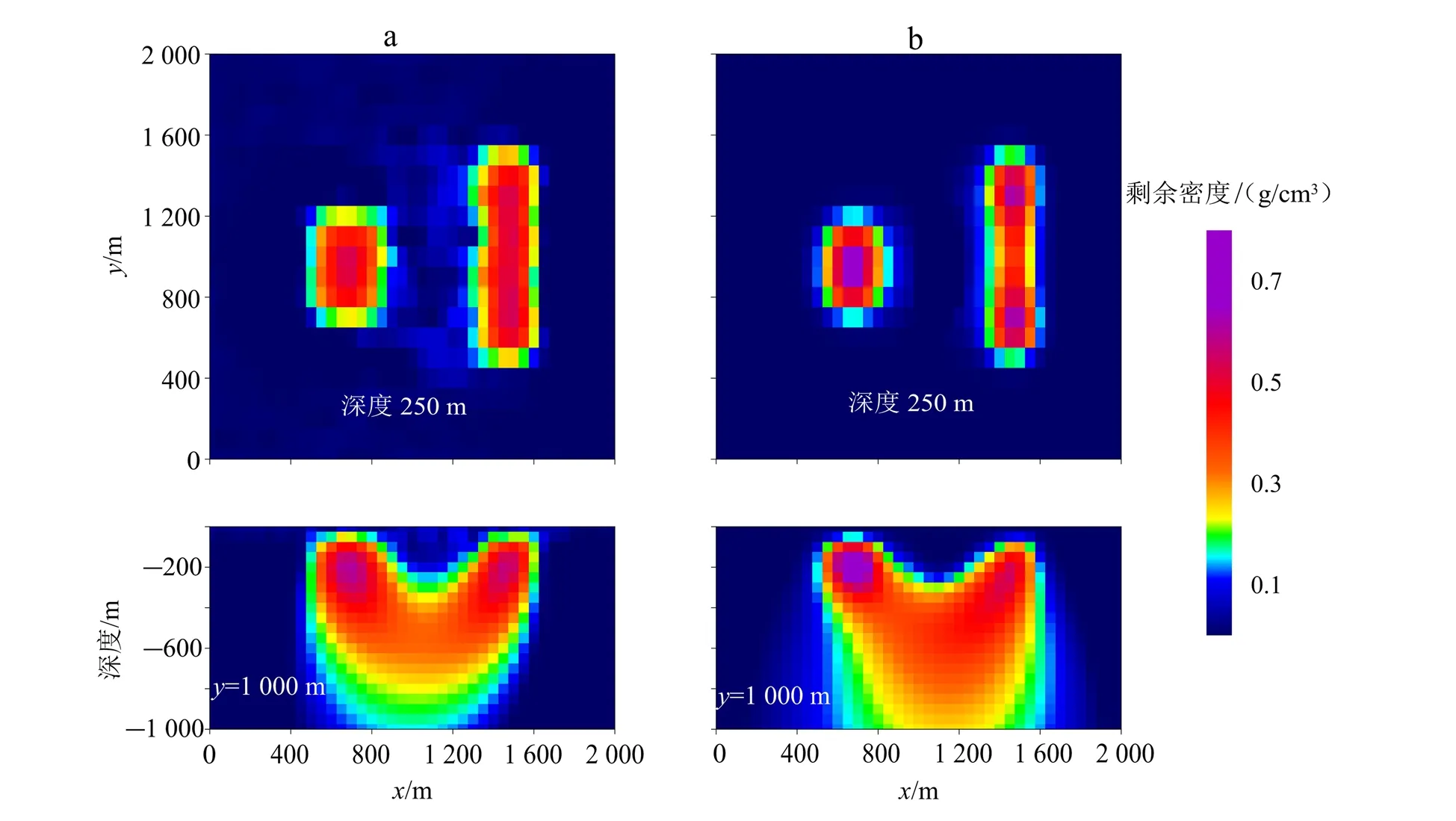
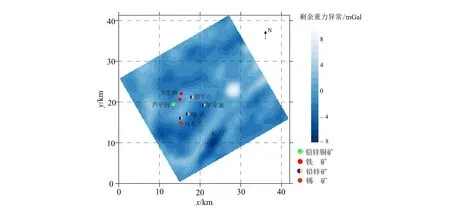
注:it为LSQR算法的迭代次数,一般而言it< 图1 理论模型Fig.1 Theory model a.深度加权;b.互相关系数加权;c.深度与初始互相关系数加权;d.反演迭代两次后的深度与互相关系数加权;e.反演迭代三次后的深度与互相关系数加权。黑色线框为理论模型。图2 理论模型不同加权结果Fig.2 Synthetic model of different weighted results 在正则化反演过程中,拉格朗日因子(正则化因子)体现了模型约束与数据拟合之间的平衡:过大的拉格朗日因子往往偏重于模型约束中各单元体的重要性,而忽视了数据的拟合程度,会使得迭代收敛缓慢,甚至于出现不收敛的情况;过小的拉格朗日因子则偏重于数据拟合,而忽视了模型各单元应有权重的影响,会使得反演出现过拟合现象,无疑增加了解的非唯一性,使得求解结果不够稳定。目前常用的拉格朗日因子求取算法有广义偏差准则、广义交叉验证准则和L曲线法,3种计算方法都包含了大规模矩阵的多次计算,无疑增加了计算成本。本文拉格朗日因子求取采用在一定步长下逐次递减的方法[27],当出现迭代发散时,拉格朗日因子相应地增大并重新求解。该方法求解过程较为稳定,且避免了多次拉格朗日因子搜索所需的额外计算成本。 由于核矩阵为大型稠密的,直接法求解式(3)或式(4)的计算成本巨大。Krylov子空间迭代法仅出现矩阵与向量的乘积,具有收敛速度快、对计算机内存要求低等优势。CGLS(共轭梯度最小二乘法)和LSQR算法同属于Krylov子空间投影方法,两者的运算量与存储量相当,但当执行多次迭代或系数矩阵为病态时,LSQR的数值稳定性更好[16]。 因此,我们引入LSQR算法求解反问题。令A*=AD-1,Δm*=DΔm;由于D为对角矩阵,有D-1D=I,则式(2)可写为 (7) 此时式(7)为阻尼最小二乘法,可引入阻尼LSQR算法求解线性方程组问题。在求得Δm*后,根据Δm=D-1Δm*反求模型修改量。 方程A*×Δm*=Δd关于阻尼因子λ最小二乘问题的LSQR算法见表2[28]。 表2 阻尼LSQR算法 由上述阻尼LSQR算法可见,它仅涉及到矩阵与向量的乘积。若将A*按列划分为k个子矩阵,且向量b(表2中的μi或νi)及子向量bi的阶数与对应的矩阵及子矩阵列数一致,则有: (b=[b1,b2,…,bk]), 假设面积数据是网格化水平分布的,并且模型剖分单元与数据网格采取一一对应的关系,则根据平移等效性和互换对称性,在同一层模型各单元之间,核矩阵A的元素具有特定的规律,即等效几何格架;实际中只需计算和存储每一层的第一个单元在所有观测点处的重力响应核函数,同一层的其他元素可根据下式进行索引查找[2]: A(k,l),(i,j)= A(k-i+1,l-j+1),(1,1)。 (8) 式中:i、j为任意模型单元在x方向和y方向上的排列号;k、l为任意数据观测点在x方向和y方向上的排列号。 若子矩阵按照模型单元划分,根据式(8)可快速获取某个模型单元在所有观测点处的重力响应核函数。大型稠密系数矩阵不再被完整地表示出来,且由于D为对角矩阵,不会明显增加额外的计算量,实现分块矩阵LSQR方法与等效几何格架技术的结合。 在具体计算成本方面,分块矩阵LSQR方法的空间复杂度仅为O(2M+2N),时间复杂度为O(2itMN),由于一般情况下迭代次数i远小于数据量N和模型量M,相比直接法求解式(3)、(4),分块矩阵LSQR方法节省了大量存储空间和计算时间(表1)。假设测区网格数据为100×100的规模,模型为100×100×50的三维网格,LSQR迭代次数为5 000次,则分块矩阵LSQR方法的计算量不到数据空间的一半,反演速率至少提高了2 倍;假设数据以双精度存储,则模型空间求解需1.89 TB存储量,数据空间求解需75 GB存储量,分块矩阵LSQR方法则仅需约8 MB存储量,在普通计算机上就能实现较大规模的三维反演计算。 理论模型及数据密度、网格剖分等见2.2节。我们分别利用Ddepth和DωDdepth对模型进行约束反演,附加密度约束范围为0~1 g/cm3,最终迭代反演的均方误差分别为0.031、0.112 mGal。 图3a、b分别为利用Ddepth和DωDdepth进行模型约束的反演。两种模型约束的反演异常在浅部差别不大,但在深度为400 m以下则差别逐渐变大:利用Ddepth进行模型约束的反演异常呈较正的“v”字型(图3a),这与真实模型不一致;而利用DωDdepth进行模型约束的反演异常呈“y”字型(图3b),较清晰地反映了真实异常体的基本轮廓。 a.利用深度加权函数进行模型约束的反演结果;b.利用互相关系数与深度加权进行模型约束的反演结果。图3 理论模型两种约束方法的反演结果对比图Fig.3 Comparison of the inversion results of the synthetic model with two model constraints 芦子园铁铅锌铜多金属矿位于保山—镇康地块的南端,成矿类型为岩浆热液型,已有地质、物探及化探工作均认为该区成矿作用与隐伏中酸性岩体密切相关[29]。但由于矿区地表未见岩体出露,且在矿区南东部出露的印支期木场花岗岩体与成矿作用无明显关系,因而针对岩体的研究总体较少,譬如岩体的埋深、规模及其空间形态等均鲜有研究。区内主要出露寒武系、奥陶系、志留系、泥盆系、石炭系、二叠系的碳酸盐岩、碎屑岩,石炭系、三叠系的火山岩以及第四系。物性资料(图4)表明:木厂出露的花岗岩体密度常见值为2.59 g/cm3,明信坝出露石英闪长玢岩密度常见值为2.66 g/cm3,两者相对于区内广泛出露的碳酸盐岩(密度通常在2.73~2.75 g/cm3)围岩表现为低密度特征。在不同类型岩石中,泥岩、粉砂岩密度最小,其次为中酸性岩体,矽卡岩化、矿石以及火山岩密度最高,碳酸盐岩密度居中;区内第四系以及新近系、古近系、白垩系和侏罗系规模有限。综合密度测试结果可知,重力测量在区内寻找隐伏中酸性岩体具备较好的物性条件。我们以云南地质调查院提供的芦子园地区1∶5布格重力数据为例,进行三维反演以推测区内隐伏中酸性岩体的空间分布特征。 图4 云南芦子园地区岩石密度测试统计结果Fig.4 Statistical results of rock density in Luziyuan, Yunnan 反演前采用矩形窗口滑动平均法求取剩余重力异常(图5)。利用网格化的剩余重力异常数据进行三维反演,共4 148个数据,模型水平方向剖分与数据一一对应,垂向剖分34层,共141 032个网格单元。在普通Thinkpad台式机电脑上(处理器:Intel i5-2400CPU,3.10 GH;内存:4 GB)反演迭代3次,共耗时51 h 54 min,最终反演的均方误差为0.104 mGal。 由于中酸性岩体表现为低密度,为方便起见,我们只提取三维反演结果的低密度体(根据物性测试统计结果,并结合MT测量与密度成像结果的形态特征[30-31],低密度体取剩余密度小于0.1 g/cm3),并将其套合在地质图上(图6)。由于区内砾岩、砂岩、粉砂岩等低密度体规模有限,且表现为低电阻率特征,而中酸性岩体表现为高电阻率特征,结合MT测量结果[30-31]以及其他地质、物探、化探[29-32]证据,推测这种大规模低密度体主要反映了中酸性岩体。 图5 云南芦子园地区剩余重力异常图Fig.5 Residual gravity anomaly contour of Luziyuan, Yunnan 1.第四系砂、砾、黏土;2.新近系南林组砾岩、砂岩、粉砂岩;3.古近系勐腊组砾岩、砂岩、泥岩;4.白垩系南新组砂砾岩;5.侏罗系中统粉砂岩、页岩;6.三叠系粉砂岩、灰岩、玄武岩;7.二叠系灰岩;8.石炭系玄武岩、灰岩;9.泥盆系灰岩;10.志留系栗柴坝组灰岩;11.奥陶系灰岩;12.寒武系上统碳酸盐岩;13.碱长花岗岩;14.铁矿;15.铅锌矿;16.铅锌铜矿;17.锡矿;18.推测中酸性岩体。图6 云南芦子园地区地质及重力三维反演结果图Fig.6 Results of 3D gravity inversion and geology of Luziyuan, Yunnan 由图6可见:研究区外围南东部出露的印支期木场花岗岩体与反演结果的南东部低密度体在平面位置上一致,总体倾向南东,显示与成矿作用关系不大,这与地质、化探认识一致;而研究区北东的低密度体在总体趋势上与镇康复背斜一致(走向北东),显示复背斜对岩浆侵位的控制;已知矿床在平面位置上均位于岩体形成的凹入部位或转折部位,为岩浆热液成矿的最有利地段,其中,芦子园、天生桥一带的侵入岩枝隆起中心为天生桥,并向芦子园矿段侧伏,这与天生桥到芦子园的“背形”隆起条带状矽卡岩型磁铁矿(铁矿体自天生桥向芦子园呈隐伏延伸,埋深逐渐加大)形态一致。根据上述推断的岩体空间分布特征与已知地质信息[29-32],显示了本算法的实用性。 1)将拟合残差计算所得的互相关系数作为先验信息,与深度加权函数同时引入正则化反演模型约束中,既体现了互相关系数在模型约束中的作用,又不至让反演结果过分依赖于互相关系数。理论模型反演结果表明,这种自约束反演方法对真实异常体的轮廓反映较为清晰,解模型更加符合实际情况。 2)引入阻尼LSQR算法求解反问题,由于一般情况下迭代次数远小于数据量和模型量,反演速率可提高数倍。算法中只涉及到矩阵与向量的乘积,便于实现分块运算,结合等效几何格架技术,将原矩阵按照模型单元划分为若干个子矩阵进行存储与运算,极大地节省了反演对计算机存储空间的需求。 3)将本文的重力三维反演方法应用于云南芦子园隐伏花岗岩体的定位中,共4 148个数据,141 032个模型单元,在普通计算机上运算仅需约52 h。反演结果显示已知矿床均位于推测岩体形成的凹入部位内侧,为岩浆热液成矿的最有利地段,验证了方法的有实用性。 致谢:王永华教授在程序编写及论文撰写期间提供了帮助,在此表示感谢。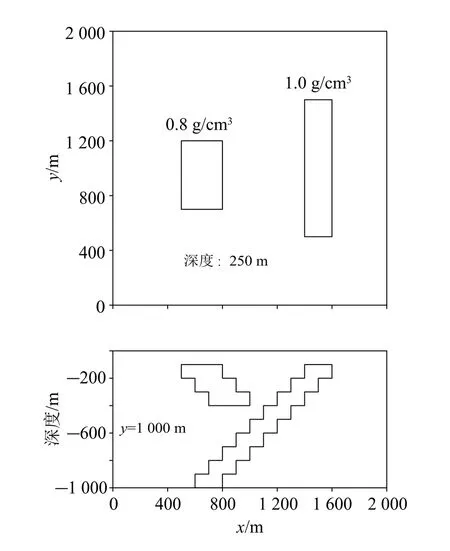
2 分块矩阵LSQR方法
2.1 阻尼LSQR算法


2.2 系数矩阵分块运算
3 反演实例
3.1 理论模型
3.2 实例


4 结果与结论
