一种利用矢量-角度法的模型点云压缩算法
2018-10-09刘继庚王晓红王东东邓仕雄闫星光
刘继庚,王晓红,王东东,邓仕雄,闫星光
(1. 贵州大学矿业学院,贵州 贵阳 550025; 2. 贵州大学林学院,贵州 贵阳 550025)
三维激光扫描技术的快速发展使其在文物保护、数字城市、逆向工程等领域得以应用[1-6],但其海量的数据包含大量的冗余信息,带来数据处理和存储的难题[7]。因此,在保证一定精度的前提下,对海量点云数据进行压缩是必要的。目前点云压缩算法主要有2种:直接基于点云的压缩和基于网格的压缩[8]。前者直接根据点云空间拓扑关系计算对应的离散几何信息对点云进行精简处理,但压缩数据在细节特征上容易损失[9-10]。基于网格的压缩需要构建三角网格,而这是一项耗时复杂的工作,效率低下[11-13]。本文基于切片技术[14-15]提出一种新的自适应点云压缩算法。该算法基本思路为,先将点云进行分层形成点云切片,在此基础上使用矢量-角度法逐层进行点云压缩。
1 算法介绍
1.1 自适应切片点云生成
形成点云切片的基本步骤是建立点云的最小包围盒,通过分割包围盒得到小分割块,在每个分割块上建立切片点云。算法流程如图1所示。
1.1.1 包围盒的初步分割
最小包围盒是在三维坐标系中将模型包含在内的最小立方体。假设点云集为p={p1,p2,…,pn},pi为(xi,yi,zi)∈R3。最小包围盒通常按照模型坐标的最大值和最小值确定,即为|xmax-xmin|、|ymax-ymin|、|zmax-zmin|,那么形成最小包围盒B=[xmin,xmax]×[ymin,ymax]×[zmin,zmax],分割方向可以自定义,一般沿坐标轴进行分割。若沿z轴分割包围盒,将最小包围盒B作均匀分割,得到n个平行的小长方体Bzi,i=0,1,2,…,n-1。由于初始分割没有考虑点云密度变化的问题,接下来要对密度过大的分割块进行迭代分割。

图1 自适应切片算法流程
1.1.2 对包围盒进行迭代分割
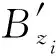
1.1.3 点云切片的建立
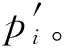
1.2 矢量-角度法
点云切片数据属二维数据,这样就简化了下一步的压缩运算。如果单独使用角度阈值进行数据精简,当2个点相距较远时,即使夹角很小,最短距离也可能很大,这时不能单凭角度就将其删除;当2个点相距较近时,最短距离很小也可能有较大的夹角,这时也不能由于最短距离小而将其删除。因此,采用矢量-角度法能克服上述缺点,快速有效地精简数据。矢量-角度法示意图如图2所示。
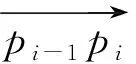
(1)
由向量的方向性可知,根据r值的不同,最短距离d可以计算为
(2)
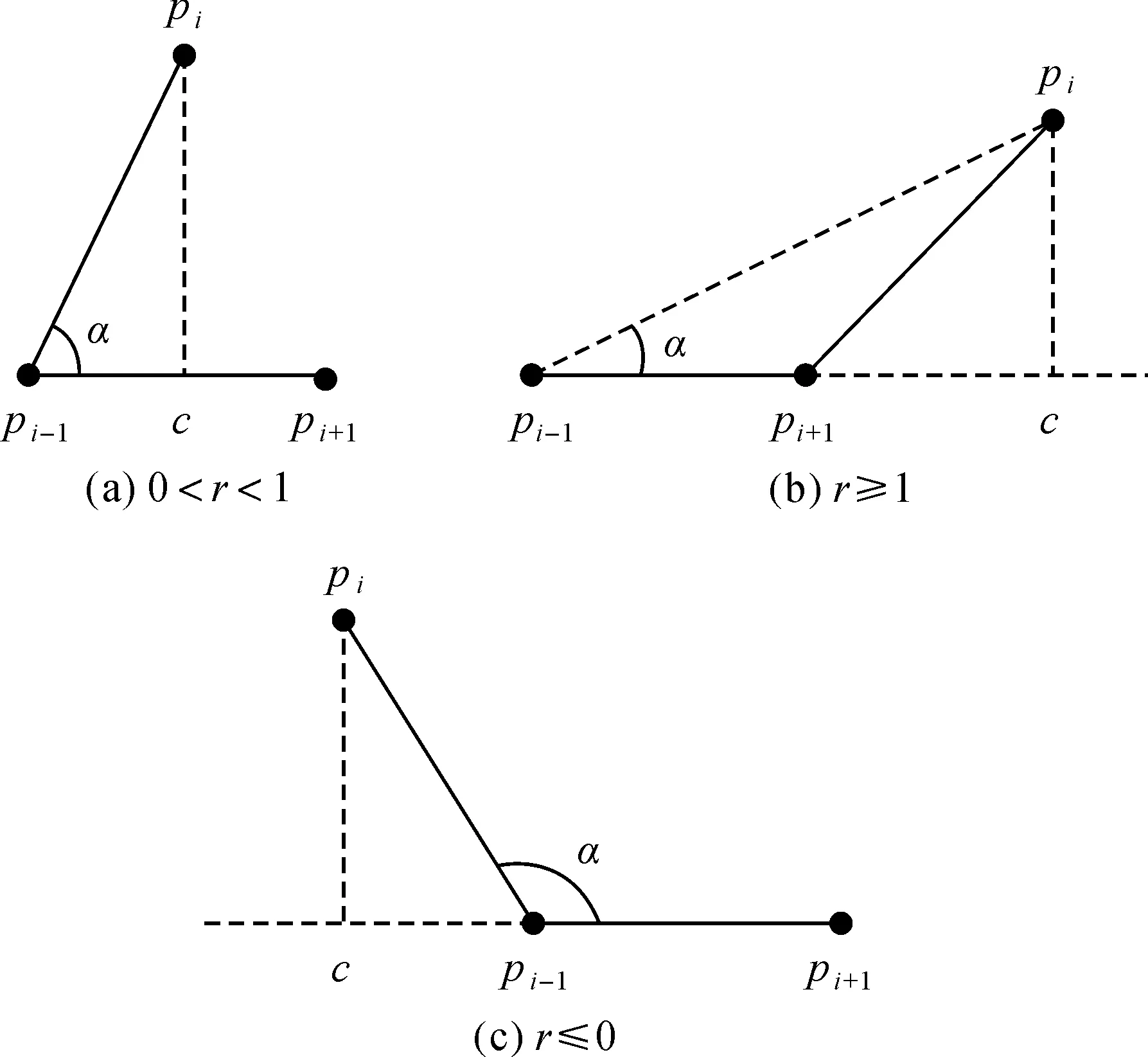
图2 矢量-角度法
当夹角大于或小于所设的夹角阈值,或最短距离小于所设阈值时说明形状变换平缓,应当删除该点。当某点满足以下2个条件之一时,说明该点处形状变换平缓,应当删除该点:一是最短距离小于所设阈值;二是夹角小于或大于某个阈值(本文把该阈值称为特征角度)。自定义的阈值参数可由不同的指标定义,由图2可以看出,阈值的取值决定压缩率和压缩质量。当阈值过大时删除的数增多,此时只有形状变化剧烈的地方才能保留较多的点,很多细节和小特征将丢失;当阈值过小时,删除的点数变少,得不到理想的压缩效果。因此,选取适合的阈值在提高压缩率的同时保证重要细节特征非常关键。
本文用点云数据分层后每层的最短距离均值分布选取阈值,角度阈值通过试验予以给定。每层的最短距离均值由式(3)计算得到
(3)
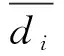
2 算法实现及对比分析
本文试验的硬件环境为Intel i3-2310处理器、6 GB内存,软件环境为VS2015、PCL点云库。试验数据采用从Leica官网下载的Gate点云数据,原始点云总共包含320 557个点。
2.1 确定分层数目
初始分层数目对最终的分层结果,以及执行时间和压缩率有比较大的影响,由于阈值参数对分层结果没有影响,本文随机选取了一个角度阈值进行试验。图3为设定角度阈值为α>140°或α<40°时使用不同分层数对Gate点云模型压缩的结果。
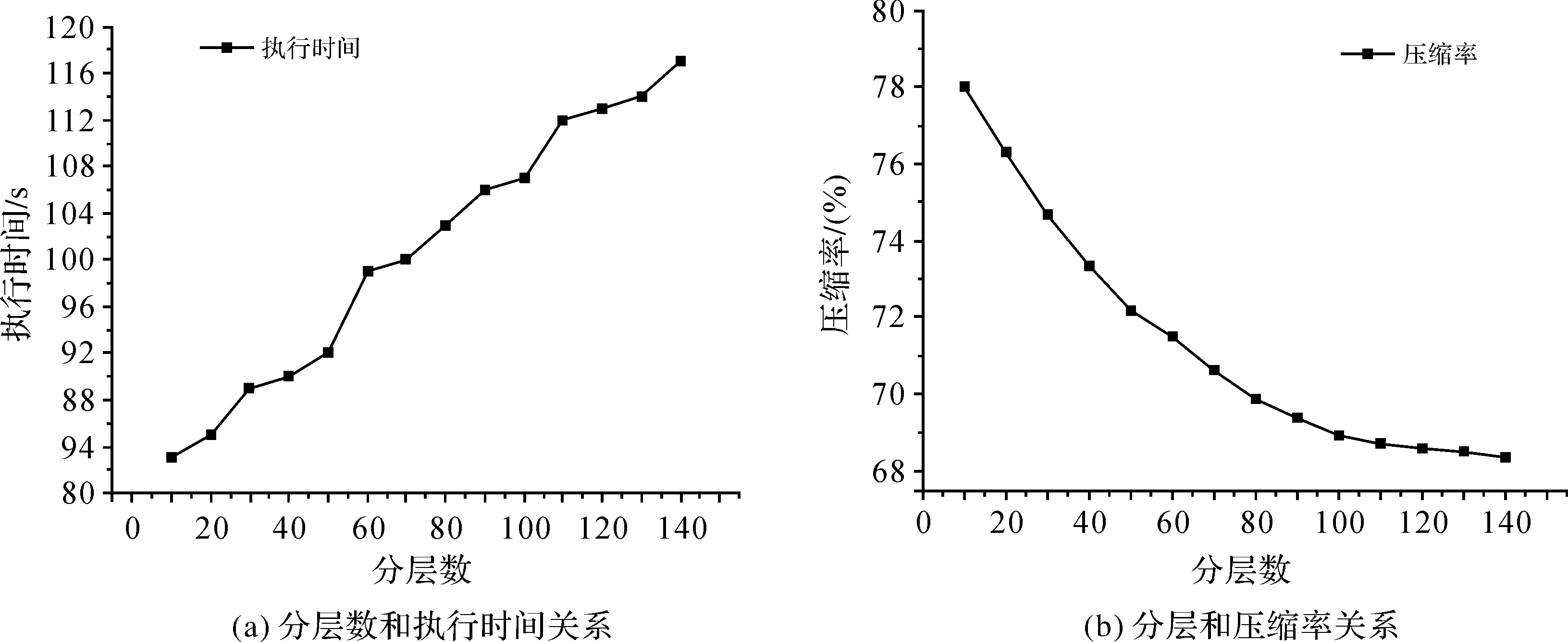
图3 模型分层数与时间、压缩率的关系
从图3可以看出,算法的执行时间随着分层数目的增加而随之增加,压缩率随着分层数的增加而逐渐减少。图3(a)是分层数和执行时间的关系,当分层数比较小,如30~90层时随着分层数的变大执行时间急速增大;大于100层后随着分层数的增加执行时间小幅增加;大于110层时执行时间的增幅趋于稳定。图3(b)是分层数与压缩率的关系图,当分层数较小时,增加分层数会让压缩率锐减;大于100层后,随着分层数的增加压缩率小幅度降低,大于110层时,压缩率的变化逐渐趋于稳定。综合二者考虑,当分层数为100时算法有较高的效率又能保证压缩率,是试验的最适合层数。最终的分层结果如图4所示。

图4 最终分层结果
2.2 确定最短距离和角度阈值
对试验数据设定分层数为100,选取相同的角度阈值不同最短距离平均阈值进行压缩,其结果如图5所示。从图5可以看出压缩率随阈值递增呈显著上升趋势。大压缩率是算法追求的效果之一,但是在压缩率大的同时,被删除点数增多,压缩对象的细节与特征可能会有丢失,因此最短距离阈值的选取十分重要。图6为原始数据点云分层为100时每层的最短距离平均值分布情况,可以看出每层的最短距离均值最小值为0.06 mm、最大值为0.23 mm。
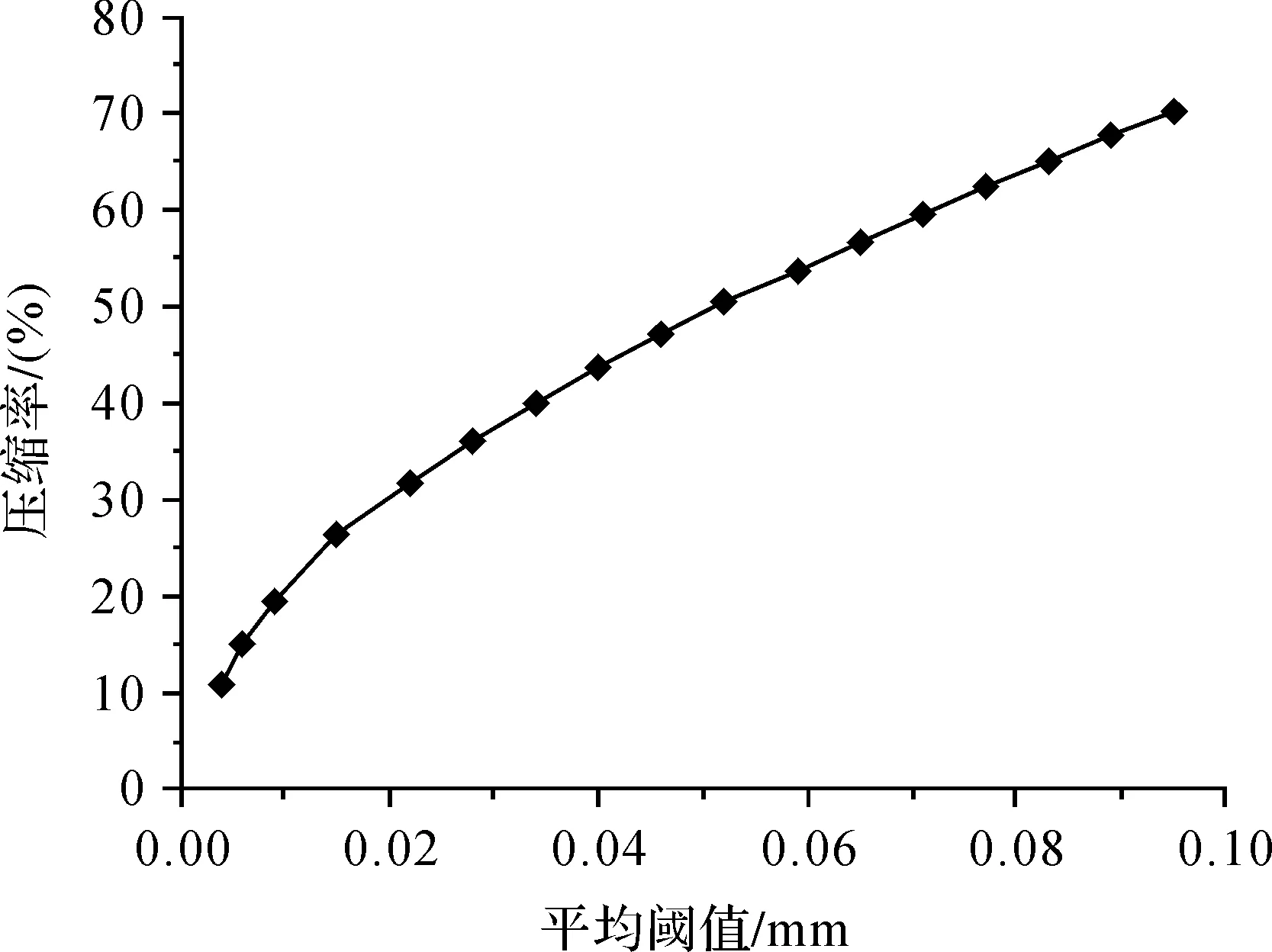
图5 平均阈值与压缩率的关系
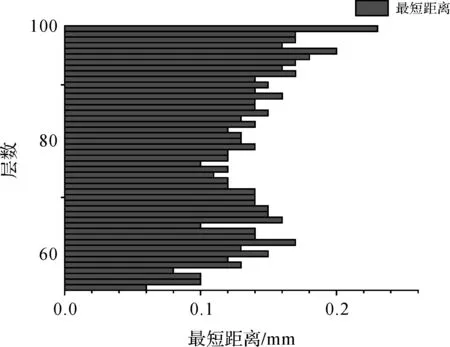
图6 每层最短距离均值分布
分别设最短距离阈值为0.05 mm(小于最短距离均值最小值)和0.2 mm(在最短距离均值最小值与最大值之间),对点云数据进行压缩,其压缩结果如图7所示。其中,图7(a)是原始点云数据,图7(b)是阈值为0.05 mm时的压缩结果,压缩率为65.41%。图7(b)中点云模型的轮廓特征,装饰纹理、雕刻纹理处仍然可以很好地表现出来,压缩效果和压缩率较为理想。图7(c)是阈值为0.2 mm时的压缩效果,压缩率为76.05%。从图7(c)可以明显看出压缩后的轮廓线已近变形,部分部位点云丢失严重。因此,为了保证压缩质量,切片点云的最短距离均值选取是重要的参考量,为了很好地保留点云特征和细节,应该选取小于该值的数作为阈值。
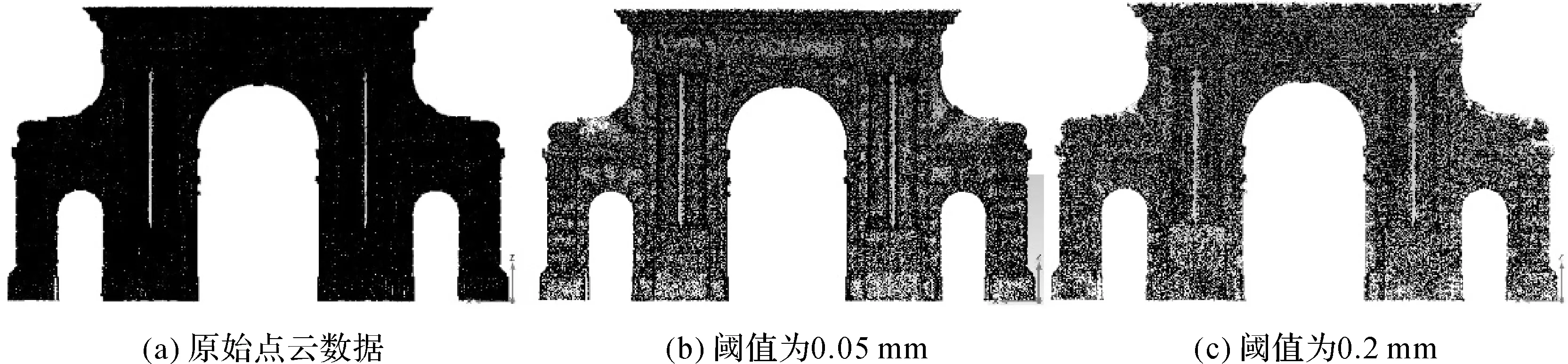
图7 原始点云与不同阈值压缩点云对比
角度对点云压缩质量有重要影响,为了得出合适的角度阈值,本文采取以下试验方式:对试验数据设定分层数为100,取不同的角度阈值进行压缩,通过分析角度和时间(压缩率)之间的关系确定适合的阈值,结果如图8所示。从图8(a)可以看出压缩率随着特征角度的增大逐渐降低,特征角度α>140°或α<40°时(对应图8横坐标3),随着特征角度的变化压缩率变化趋势逐渐放缓。图8(a)横坐标值为0°时,只把最短距离作为阈值进行点云压缩,可以看出相比有角度阈值时压缩率急剧下降,并且从图8(b)可以看出只有最短距离阈值的压缩时间和角度-最短距离阈值相差不多。试验结果表明α>150°或α<30°(对应图中横坐标4)为最适合的角度阈值。
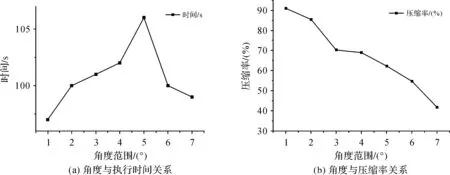
注:图中横坐标1—7分别代表特征角度α>120°或α<60°、α>130°或α<50°、α>140°或α<40°、α>150°或α<30°、α>160°或α<20°、α>170°或α<10°、α=180°。图8 角度与压缩率、时间的关系
2.3 压缩结果比较和评价
点云精简评价多采用目视的方式,也可用体积变化率进行压缩效果评价,本文采用这两种方式对压缩结果进行评价。为了验证本文算法的优越性,在压缩率基本相同的情况下,将随机采样法、曲率法、文献[14]算法、文献[15]算法与本算法进行比较,各算法压缩结果见表1,点云压缩效果和建模效果如图9、图10所示。
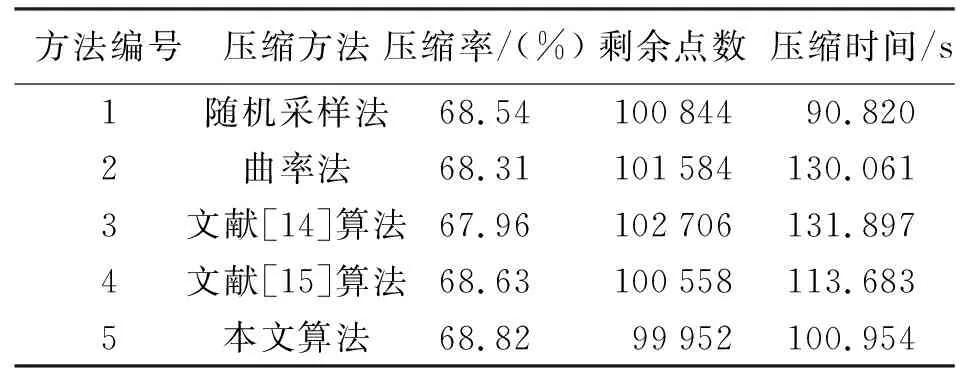
表1 Gate模型不同压缩方法对比结果
通过表1、图9和图10可知,本文算法在既没有大的形状变化也没有小特征的平坦处保留较少点,在形状变化剧烈及细节特征很多处,保留了大量的点。通过和原始点云图9(a)对比不难发现本文算法能保证在较高压缩率的情况下自适应地删除点,即根据点云模型的特征在平坦处删除大量的点,在特征处保留大量的点,这样不但保证了点云压缩的效率而且很好地保留了点云模型的特征,并且花费时间相对较少。对压缩后的点云进行建模时,本文算法基本没有出现孔洞,而且在柱体花纹、门洞弯曲处、大门左右雕刻处等特征部位保留了更多的细节,建模结果与原始点云基本没有区别。其他4种方法在不同部位过度压缩产生了孔洞,而且细节特征有着不同程度的丢失。

图9 原始点云与压缩点云对比

图10 原始点云与压缩点云建模对比
3 结 语
针对点云数据量大,冗余数据多,影响点云数据后续处理的问题,本文结合包围盒理论,提出了基于自适应切片点云的矢量-角度法实现对点云的压缩。该压缩算法的分层数与算法执行时间和压缩效率相关,角度和最短距离阈值的取值大小决定特征细节点的保留与否。本文通过试验确定了点云压缩的最短距离和角度参数的最佳取值,利用该算法对Gate点云数据进行压缩,并对压缩结果进行分析,结果表明,该算法在快速压缩的同时具有较高的压缩率,并且能够很好地保留原模型的细节特征信息。
