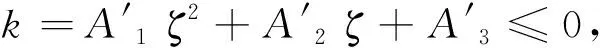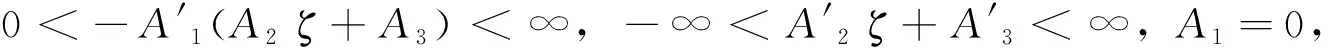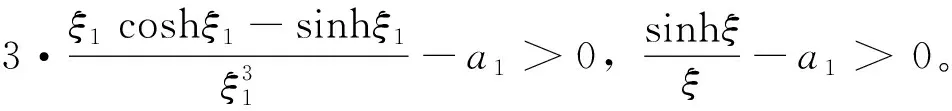具有第三边界坏死核肿瘤数学模型稳态解的存在唯一性*
2018-10-09沈海双卫雪梅刘成霞冯兆永
沈海双,卫雪梅,刘成霞,冯兆永
(1. 广东工业大学应用数学学院,广东 广州 510520;2. 南方医科大学口腔医院,广东 广州 510280;3. 中山大学数学学院,广东 广州 510275)
在20世纪70年代,Greenspan[1-2]提出早期肿瘤的生长规律是可描述为偏微分方程组的自由边界问题。Friedman等[3]开创性地研究了无死核肿瘤的第一边界问题的数学模型;Cui等[4]考虑了带抑制物的模型;Friedman等[5-6]则研究了无死核肿瘤的第三边界问题。这些文章用严格的数学分析,分析了稳态解的存在唯一性,整体解的存在唯一性和解的渐近性态。文献[7-8]则应用抛物型方程的Lp理论、Schauder估计、比较原理、Banach不动点定理和延拓法,证明了模型整体解的存在唯一性。
在文献[9]中,Byrne 和Chaplain 在肿瘤形状为球形并且肿瘤有坏死核的条件下,提出来下述在营养物作用下肿瘤生长的数学模型:
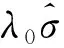
根据文献[9],初边值为:
在文献[9-10]中:
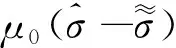
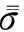
为方便研究,取μ0=1并采用变量替换:
则模型简化为:
0
(1)
(2)
(3)
σ(r,t)=σ0, 0≤r≤ρ(t),t>0
(4)
(5)
(6)
(7)
σ(r,0)=σ0, 0≤r≤ρ(0)
(8)
假设(σs(r),ρs,Rs)是模型(1)-(8)的稳态解,即满足以下方程:
(9)
(10)
(11)
σs(r,t)=σ0, 0≤r≤ρs
(12)
(13)
(14)
显然有

(15)
再根据式(6),得
(16)
注1 模型(1)-(8)的稳态解的存在唯一性等价于式(15)-(16)解的存在唯一性。
故本文旨在研究式(15)-(16)解的存在唯一性,其主要结论为:
定理1 当ξ∈(ξ1,ξ3)时,由式(17)确定的ζ满足ζ′<0。
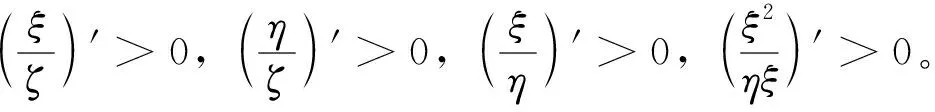

则式(15)-(16)存在唯一解。其中的ξ,η,ζ,ξ1,C(ξ1),ξ3的具体表达式参见下一节。
1 相关符号及预备引理
为叙述方便,引进一些符号:
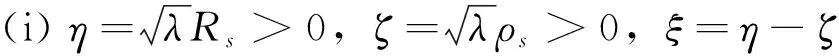

(iii)A1=a4coshξ+sinhξ-a3a4,
A2=a4ξcoshξ+ξsinhξ+a4sinhξ-2a3a4ξ,
A3=ξcoshξ-sinhξ+a4ξsinhξ-a3a4ξ2
因此,式(15)-(16)可分别等价为:
A1ζ2+A2ζ+A3=0
(17)
ξcoshξ-sinhξ+(sinhξ-a1ξ)ζ2+
(18)
并设
f(ξ)=ξcoshξ-sinhξ+(sinhξ-a1ξ)ζ2+
(19)
我们给出几个预备引理:
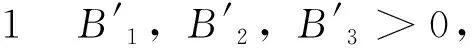
引理2 (i) 当1 证明(i) 当1 故引理2均得证。 引理3 存在0<ξ1<ξ2<ξ3,使得B1(ξ1)=B2(ξ2)=B3(ξ3)=a3,即 A1(ξ1)=A2(ξ2)=A3(ξ3)=0 根据引理2、引理3可知满足式(15)-(16)的ξ∈(ξ1,ξ3)。 注2 引入简记符号 C(ξ3)= 证明当ξ∈(ξ1,ξ3)时,即a3a4 a4ξsinhξ-2a3a4> ξcoshξ+sinhξ+2a4coshξ+a4ξsinhξ- 2a4coshξ-2sinhξ= ξcoshξ-sinhξ+a4ξsinhξ>0 证明 由于 证明当ξ=ξ3时,A1>0,A2>0,A3=0,有 定理1的证明以下分三种情况证明: (i) 当ξ∈(ξ1,ξ2)时,对式(17)式两边求导,可得 即 故有 综上所述,且ζ′显然连续,故当ξ∈(ξ1,ξ3)时,由式(17)确定的ζ满足ζ′<0。 定理2的证明:由定理1可知当ξ∈(ξ1,ξ3)时,ζ′<0,故 定理3的证明:式(19)可改写为 (20) 由引理6,得 又 结合引理5,可知 因此,式(15)-(16)式至少存在一个解。 因此,式(15)-(16)存在唯一解。
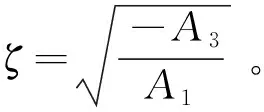

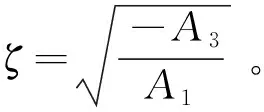


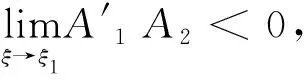

2 稳态解的存在唯一性