构造一元二次方程解题探究

安徽省阜阳市第十九中学 许明坤

在很多数学问题中，涉及的内容看似和一元二次方程无关，我们解题时如果仅仅局限于这道问题涉及的知识，总是很难找到解题的突破口，有时甚至无从下手，但经过仔细分析，我们总能与一元二次方程的知识联系起来，此时可利用题中的条件将问题转化为一元二次方程来解决，本文就构造一元二次方程解题的各种类型进行总结分析。

一、构造方程解求值问题

思路分析：从表面上看这道题与一元二次方程的联系不明显，采用“反客为主”的观点观察已知条件，会发现若将常数 视为未知数，可知 是方程的一个根。

解：显然x＝1 也是该方程的一个根。

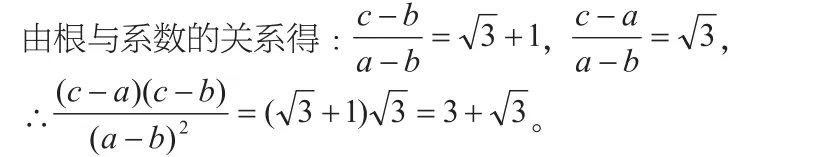
要点总结：这道题的解法新颖，利用了逆向思维的数学思想，方法非常巧妙。

二、构造一元二次方程解方程组

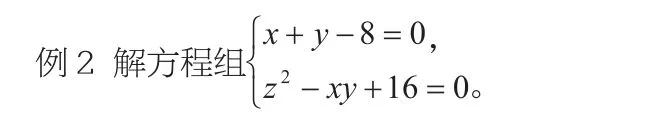
思路分析：该方程组有三个未知数而只有两个方程，又是二次的，实质是一个不定方程问题。观察方程组的特征中有x+y，xy。由此可把x，y视为关于t的一元二次方程t2-（x-y）t+xy=0的两根，利用判别式非负即可解决。

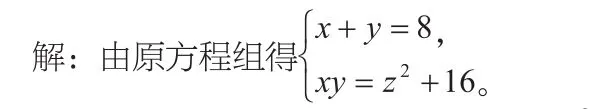
可把x，y视为关于t的一元二次方程t2-8t+（z2+16）=0的两根。

由Δ=(-8）2-4（z2+16）≥0得-4z2≤0，∴z2≤0。

又z2≥0，∴z=0，此时x＝y＝4。

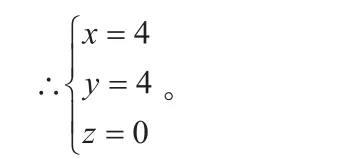
要点总结：方程组看似和一元二次方程没有关系，从条件中我们可以利用一元二次方程为解题找到突破口。

三、构造一元二次方程求最值

例3 已知x，y，z均为非负实数且x+y+z=1。求（z-x）（z-y）的最值。

思路分析：根据非负实数这个条件及所给等式与一元二次方程相结合即可解题。

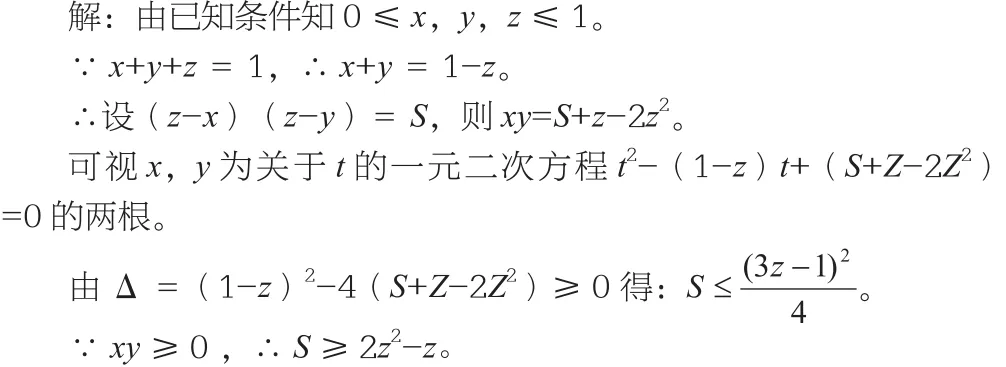
要点总结：本例题给出的是求最值，易将求最小值弄丢。仅用根的判别式不能完成解答，与一元二次函数的最值相结合，是一道很好的综合题。

四、构造一元二次方程证明不等式

例4 已知a，b，c为实数，求证：（a-b）2≥（c-2a）（2b-c）。

思路分析：由要证的不等式的特点可联想一元二次方程根的判别式，由此可用构造方程解决。

要点总结：利用构造方程后，易丢掉分类讨论，要注意思维的严密性。

五、利用构造一元二次方程证明几何问题

例5 如图：过正方形ABCD的顶点C任作一条直线与AB，AD的延长线分别相交于点P，Q。证明：

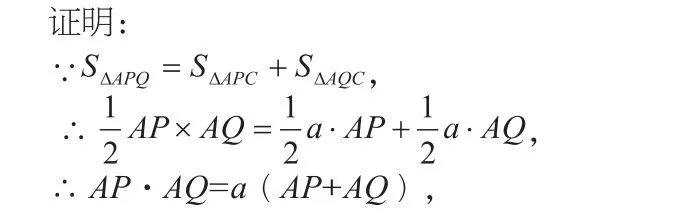
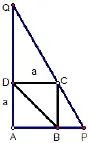
∴AP，AQ是方程x2-（AP+AQ） x+a（AP+AQ）＝0的两个实根。

由根的判别式非负可得：（AP+AQ）2-a（AP+AQ）≥0，

即 AP+AQ≥4a，

要点总结：用构造方程法还可以解决存在性问题及几何等式等，限于篇幅在此不做赘述。

运用构造法解题，首先要认真分析题目，仔细观察，展开联想，从中发现可用构造法因素；其次，借助与之相关的知识构造所求问题的具体形式；最后，解出所构造的问题，但必须回到原来的问题上。在学习过程中加强知识的综合运用，注意思维的多样性，把握解题方法的灵活性，提高数学素养和思维品质，从而达到培养创新能力的目标。