基于建构主义的数学解题教学案例分析
2018-10-08付敏
付敏
(南昌市第十中学,江西南昌 330006)
1 教学课题
本文选取的教学课题是函数值范围问题的求解。
2 教学目标
(1)理解函数中自变量与函数值的相互对应和制约关系。
(2)创设问题案例,通过启发来诱导学生发现数学逻辑错误和矛盾,通过由特殊到一般、从具体到抽象,深刻剖析错误原因,培养学生数学思维能力。
(3)通过对学生学习认识策略的指导,培养学生学习反思的良好思维习惯,发展学生智力。
3 教学重点、难点
重点:掌握求函数值及其范围的方法。
难点:理解该方法的原理及内涵。
4 教学方法
本文选取的教学方法是建构式教学法。
5 学生的现状
已学好函数的概念,理解自变量与函数的相互关系及函数值的求法,并能运用函数的知识去解决简单求值问题的高一年级学生。
6 教学过程
6.1 案例呈现
如下一个数学问题:
已知:f(x)=ax2-c, 且 -4≤f(1)≤-1,-1≤f(2)≤5
求:f(3)的取值范围。
有相当一部分同学求解如下:

(设计意图:学生用认知结构中已有的旧知识去解决新问题时,学生往往缺乏联系和学习的积极主动性,教师采用角色换位的解题教学方法,使学生亲身经历解题的过程,让学生产生认识冲突,激发学生探知的强烈欲望,对问题进行“理解”与“消化”达到数学信息多角度的表征。)
6.2 解题策略指导
教学中,该问题(学生的解题思维过程)提出来,供大家讨论,同学们学习兴趣十分高涨,这时,采取对学生积极引导并提出如下质疑:(1)上述问题推理过程是否正确?其推理理论依据是什么?(2)其思维过程是否为等价转化?(3)请你用尝试方式验证结论的极端值是否正确。(4)综上分析,你的最终结论是什么?
学生一般都经历先认为原解法正确再否认的思维过程。其主要思维体现如下:对于引导①,由于理论明显,都归因于不等式的性质。对于引导②,由于暂时性地无法发现错误,很多同学都认为过程为等价变形。待引导③出现之后,大部分学生思维开始又活跃起来。他们积极从如下思考:
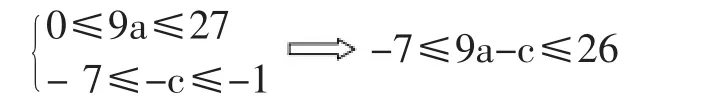
当 f(3)=26 时,当且仅当 9a=27,-c=-1
此时 a=3,c=1 从而 f(1)=a-c=2∈[-4,-1]
f(2)=4a-c=11∈[-1,5]
与条件矛盾,可见f(3)不可能到26
当 f(3)=-7 时,当且仅当 9a=0,-c=-7
此时 a=0,c=7,从而 f(1)=a-c=-7 ∈[-4,-1]
f(2)=4a-c=-7∈[-1,5]
也与条件矛盾,可见f(3)也不可能到-7
至此,大家一致认为解答有误,可原因在哪儿呢?
(设计意图:实现学习活动及其构成也不是单纯的个人的进程,而是在于师生、学生间的共同活动,包括一起分析并寻找联系与解答,一起设计与证明,还一起检验与评估其结果,以此创设一个好的“学习共同体”。)
6.3 协作研究探索
通过上述的分析,大家质疑“不等式性质定理3的推论”在解题中使用造成的吗?故师生进入了对不等式的可加性做进一步的思考与分析。
结果发现:定理3的推论:若a>b,c>d则a+c>b+d中,条件“ a>b,c>d”是“ a+c>b+d”成立的充分不必要条件。
本题中,解题思维过程的蕴涵关系如下:
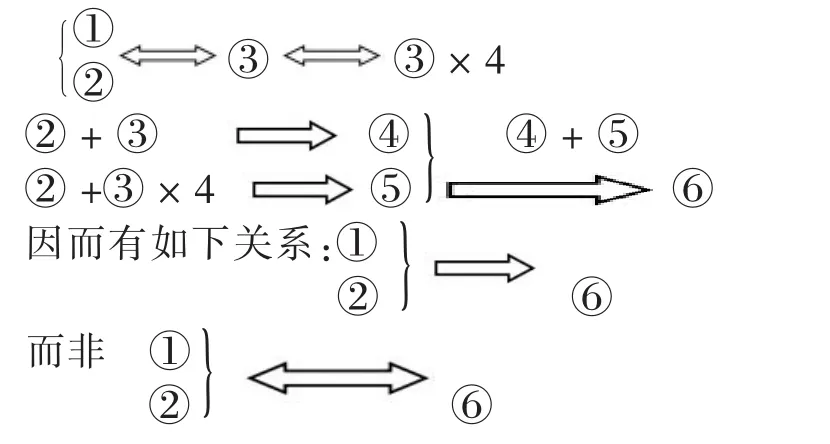
案例中所依据的理论是正确的,但由于违背了等价性的思想和原则,却将问题的范围扩大了。即上述推理虽然得出 f(3)∈[-7,26],但却不能取满到-7 到 26 之间的一切值。
(设计意图:通过对数学思维过程的分析与思考,加深了学生对数学概念理解,渗透了等价转化的思想方法,达到了实现认识整合,打破认识平衡状态的目的。)
6.4 意义建构,解决问题
我们的问题可以等价地转化为:
求 f(3)=9a-c 的取值范围。
解:设M=9a-c,从而 c=9a-M
故问题又等价转化为:过图象中的区域内EFGH的点(a,c),作斜率为9的直线,求其在c轴上的载距-M的取值范围。
显然,当过点 E(0,1),即 a=0,c=1时 -M 有最大值 1,当过点 G(3,7),即 a=3,c=7 时,-M 有最小值-20。
即有:-20≤-M≤1
∴-1≤M≤20
故所求 f(3)的取值范围为[-1,20]
(注:这里渗透了线性规划的思想和方法)
另解:令 m(a-c)+n(4a-c)=9a-c
用待定系数法,得
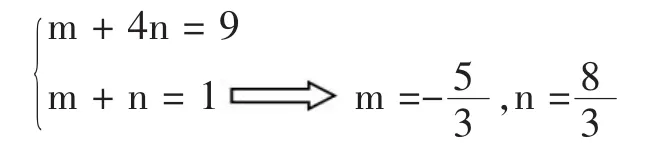
①×(-5/3)+②×8/3 得 -1 ≤ 9a-c≤ 20
∴所求范围是[-1,20]
(设计意图:循寻学生心理认识发展的规律,在学生认识经历了“平衡—不平衡”的发展变化之后,不失时机地向学生介绍正确的解题方法与技巧,同化学生的心理认识结构,达到认识的新平衡状态,顺利实现学生对新知识的心理意义建构。)
一种独立的教学模式构建,必须通过对教学模式的长期实践,笔者仅对数学解题模式做出上述初步构建,以期随着建构主义理论的深入学习与后继的教学研究实践使之完善。
