一种融合小波变换与卷积神经网络的高相似度图像识别与分类算法*
2018-10-08姜文超刘海波杨宇杰陈佳峰孙傲冰
姜文超,刘海波,杨宇杰,陈佳峰,孙傲冰
(1.广东工业大学计算机学院,广东 广州 510006;2.广东电子工业研究院,广东 东莞 523808)
1 引言
颜色、纹理特征差异度小的特定领域高相似图像识别与分类技术在图像搜索、遥感、刑侦、医学等图像处理领域具有重要的应用价值。Renninger等人[1]认为,对图像进行简单的纹理分析能够寻找到场景分类的线索,使图像识别过程和计算简单化。Benmokhtar 等人[2]融合图像的纹理和颜色特征实现足球场景分类,但该方法仅利用全局特征进行分类,其区分能力有限。图像的局部二进制模式LBP(Local Binary Pattern)[3]计算图像中“一致”的局部二进制模式,并对图像的各种模式数进行直方图统计,但是该方法对彩色图像的分类效果一般。近年来人们对遥感影像上的纹理特征采用灰度共生矩阵算法[4],该算法描述的是具有某种空间位置关系的像素之间的联合分布,可看成两个像素灰度对的联合直方图,属于二阶统计。灰度共生矩阵描述了灰度空间依赖性,表示了在一种纹理模式下的像素灰度的空间关系,但是该方法没有完全抓住图像局部灰度的图像特征,因此对于图像局部特定特征提取效果不够理想。小波变换[5,6]虽能有效提取图像局部纹理特征,但对图像全局特征无法有效捕捉,导致分类效果一般。
在后向传播BP(Back Propogation)神经网络基础之上发展起来的卷积神经网络CNN(Convolution Neural Network)[7]是一种带有卷积结构的深度神经网络。由于该网络特点是部分连接,权值共享,从而减少了网络模型参数个数,有效缓解了模型的过拟合问题。CNN通过有监督学习方式,实现图像处理中平移、缩放、倾斜等形变的高度不变性。1998年,LeCun 等人[8]将CNN用于文档识别,为了保证识别对象的平移、尺度、旋转不变性,CNN具备局部感受野、共享权值和次抽样三个特征,设计的用于字符识别的卷积神经网络LeNet-5系统在小规模手写数字识别中取得了较好的效果。
2012年,Krizhevsky 等人[9]采用称为AlexNet 的CNN,设计了ReLU作为网络卷积层中的神经元激活函数,利用 Dropout 避免过拟合问题。该网络模型对多维图像的识别效果明显,使图像可以直接作为网络模型的输入,避免了传统识别算法中复杂的特征提取和数据重建过程。近期有研究基于 Haar 小波变换和 CNN 模型的优势,提出 Haar-CNN 模型[10],Haar-CNN在自然场景图像特征提取和分类中优势明显,然而在纹理特征提取中效果并不显著。
针对以上问题,本文算法首先使用小波变换对图像数据进行预处理,将图像分解为不同的频域子图,然后计算各频域子图的能量参数作为纹理描述子。对不同类别、不同分辨率图像集进行特征提取并确定最佳纹理差异度参数阈值,将各子图能量特征归一化处理后作为卷积神经网络的输入,通过训练集调整网络权值并验证权值实际准确度,最终得到分类准确率最高的卷积神经网络模型。实验选取鸡蛋、苹果两类图像数据集作为实验数据,进行鸡蛋散养或圈养识别、苹果产地判定,实验结果表明该算法平均鉴别准确率达 90%以上。
2 算法原理
2.1 基本思路
算法基本思路如图1所示,通过融合小波变换与深度卷积神经网络进行特征提取与图像分类。

Figure 1 Basic ideas of the algorithm 图1 算法基本思路
为提高算法准确性,首先通过分割算法提取图像中的主体对象,实现图像主体与背景分离,防止图像背景对主体对象的分类造成干扰。数据预处理阶段利用小波变换进行图像分解并提取各频域子图特征,然后将小波变换的输出作为神经网络的输入,通过多次训练对网络权值参数进行优化更新,从而获取准确率最高的神经网络参数,得到最佳分类模型。
图1中,小波变换分解并提取图像特征和卷积神经网络分类器是该算法的核心模块。这个核心模块的流程如图2所示。
首先将去除背景的图像数据由设置的阈值进行灰度化处理,利用小波变换提取灰度图像的局部特征,将拥有全局特征的图像分解为多个含有图像局部特征的子图, 对子图进行纹理特征提取;其次,神经网络接收预处理后的子图特征作为输入数据,经过 5 层卷积以及 3 层池化多尺度采样,将输出归一化为一维向量;最后在数据量逐渐增大以及训练次数增加的情况下,网络权值不断更新,最终确定分类模型。

Figure 2 Flow chart of the core module图2 核心模块流程
2.2 频域子图分解与特征提取
小波变换是在傅里叶变换的基础上演变而来的,克服了傅里叶变换不能刻画时间域信号的局部特性、对突变和非平稳信号处理效果不好、没有时频分析等缺点。小波变换替换了傅里叶变换的三角函数基,将无限长的三角函数基换成了有限长的、会衰减的小波基。 图像作为二维数字信号,首先需要根据式(1)进行小波离散化。
(1)
其中,j为实验中小波变换的尺度阶数,尺度越大则子图细节越明显;k为位置变换的设置参数;x为灰度图像的向量化表示;a0是尺度函数;b0是位置参数。
利用小波变换进行快速分解的过程如式(2)~式(5)所示。
Aj(k,l)=
∑k1∑k2h(k1-2k)h(k2-2l)fj-1(k1,k2)
(2)

∑k1∑k2g(k1-2k)h(k2-2l)fj-1(k1,k2)
(3)

∑k1∑k2h(k1-k2)g(k2-2l)fj-1(k1,k2)
(4)

∑k1∑k2g(k1-k2)g(k2-2l)fj-1(k1,k2)
(5)
其中,h()与g()分别为小波变换的低通滤波器和高通滤波器。l为包含局部特征的子图数量,k1为图像数据水平方向平移相位差的倍数,k2为图像数据垂直方向平移相位差的倍数。
在每个尺度上,通过滤波即可得到一幅粗尺度图像以及三幅细节图像。根据滤波器的性质可知,其分别包含了原图像在该尺度上的竖直、水平以及对角方向的细节信息。以鸡蛋数据集为例,对其进行Haar小波变换二次分解预处理后得到的三幅子图效果如图 3 所示。

Figure 3 Sub-graph decomposition 图3 子图分解效果
2.3 卷积神经网络权值更新
本文算法的第二个技术核心是卷积神经网络的权值更新,此部分影响图像数据分类的最终结果。为了得到更高的分类准确率,本文进行了多次实验,重点在神经网络的卷积层以及池化层的权值更新部分。在卷积神经网络的每一卷积层中,前一层的特征图与一个需要通过学习得到的卷积核进行卷积计算,可得到新的特征图,如式(6)所示。

(6)

卷积神经网络神经元的灵敏度计算方法如式(7)所示。

(7)

误差代价函数为:
(8)


(9)
其中,down()表示下采样操作。
灵敏度计算方法为:

(10)
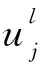
(11)
在对神经网络的卷积层以及采样层进行权值更新后,还需对其他层设置详细的优化参数,本文采用的卷积神经网络各层参数如表1所示。该网络一共包括5个卷积层、3个池化层、3个全连接层、1个softmax分类层、2个局部响应归一化LRN(Local Response Normalization)层和两个随机采样层,经过多次测试发现此参数下图像分类准确率高。其中LRN层的原理是利用仿生物神经系统抑制机制,使得函数响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,提高了模型的泛化能力。

Table 1 Structure and parameters of CNN layers表1 CNN各层结构与参数
3 实验设计与分析
实验在 Tianhe-2 上进行,采用单节点,双 CPU,24 个计算核心,内存 64 GB,即:CPU E5-2692 v2 24*2.20 GHz。采用Python3.7 以及 Matlab (2016b) 实现算法。对于鸡蛋与苹果两个数据集,通过本文算法分别鉴定鸡蛋来源是散养或圈养以及识别判断苹果产地。其中,鸡蛋、苹果数据集各包含 20 000 幅图像,训练集为15 000 幅,测试集为 5 000 幅,数据集图像标签分类标准如表2所示。

Table 2 Data classification labels表2 数据分类标签
3.1 小波变换模型与卷积神经网络模型训练
本文所定义的卷积神经网络模型的输入层的内容是由小波变换提取的保留图像纹理特征的特征向量,该向量由图像矩阵转化得到,其中去除背景的原始图像数据经由小波变换可以分解成图像近似信号的低频子带和图像细节信号的高频子带。 其中,图像中大部分的噪声和一些边缘细节都属于高频子带,而低频子带主要表征图像的近似信号。为了能够在增强图像的同时减少噪声的影响,可以对低频子带进行非线性图像增强,用以增强目标的对比度,抑制背景;而对高频部分进行小波去噪处理,减少噪声对图像的影响。然后提取各子图特征并归一化后作为卷积神经网络的输入进行进一步处理。神经网络层构建全连接池,该连接池包括 4 096 个神经元,每个神经元都连接到输入层,每个神经元接受4 096个输入。在训练过程中,记录并输出损失函数值,用以监控训练进度。将循环次数设置成 201,并且当循环次数满足10的倍数时,输出损失值。
网络结构训练过程中,从输入层到softmax层,每层都含有待求解的参数,因此利用带类别标签的数据作为输入,先进行一次前向传播,计算分类误差,然后利用随机梯度下降法进行反向传播,求解最优参数,从而使分类误差最小化。部分分类结果如图 4 所示。其中标签 true 表示分类正确(散养),标签 false 表示分类错误(圈养)。分类图像总数初始为 1 000,土鸡蛋与圈养鸡蛋的数目各为500,训练次数为500,统计可知分类准确率为 78.55%。

Figure 4 An example of preliminary classification of egg dataset图4 鸡蛋数据集初步分类结果示例
3.2 卷积神经网络模型分析
卷积神经网络模型在梯度下降处于局部收敛时,会出现分类无效的情况,即:训练过程中参数值无法保存,每次训练过程中都需要重新随机化网络模型的权值参数,多个训练集对神经网络模型的优化未发挥作用,模型应用性差。 为了能保存训练过程中的所有参数值,同类数据集测试时直接读取历史训练的参数值,实验增加两个卷积层构成卷积神经网络,在输入层和全连接层之间加入两次卷积和池化。以鸡蛋数据集为例,训练 500 次后随机抽取的部分分类结果如图 5 所示。经过 500 次的训练,算法准确率达到 86.77%。

Figure 5 An example of classification results after CNN model optimization图5 卷积神经网络模型优化后分类结果示例
为证明该算法在高相似图像识别与分类领域的准确性,选取优化后的算法对苹果数据进行测试以判断其产地。苹果数据集的数量为10 000,训练次数为1 000 次。部分分类结果如图 6 所示,对分类结果统计可知分类准确率为 87.54%。

Figure 6 Apple dataset classification results图6 苹果数据集分类结果(true:山西,false:其他)
为测试算法准确性随训练集数据量大小的变化规律,分别对鸡蛋与苹果两个数据集进行测试,数据集单位增量设置为 2 000。测试结果如图7和图8所示。由图7可知,随着数据量的增加,神经网络的参数将得到不断优化,从而有效提高了算法准确率。由图8可知,在数据集不变的前提下,随着训练次数的增加,神经网络的参数值不会陷入局部最小化,提高了全局优化效果和准确率。

Figure 7 Effect of data volume on algorithm accuracy 图7 数据量对算法分类准确率的影响

Figure 8 Effect of training frequency on algorithm accuracy 图8 训练次数对算法分类准确率的影响
为验证本文算法的优越性,将其分别与单独使用小波变换和单独使用神经网络的分类算法进行比较,平均准确率对比如表3所示。由表3可知,卷积神经网络算法在训练次数较小的情况下(10 000 次以下),多次实验后的算法准确率在 0.80~0.85变动,训练次数达20 000 次时,准确率达到最高90.06%。融合小波变换和卷积神经网络的图像分类算法具有更高的分类准确率。

Table 3 Algorithm accuracy comparison表3 算法分类准确率对比
4 结束语
针对颜色、纹理特征差异小的特定领域高相似度图像识别与分类问题,本文提出了融合小波变换与卷积神经网络的高相似度图像识别与分类算法。运用小波变换先对图像进行频域分解预处理,根据小波的多分辨率分析原理将图像进行多级二维离散小波变换,可以将图像分解成图像近似信号的低频子带和图像细节信号的高频子带。其中,图像中大部分的噪声和一些边缘细节都属于高频子带,而低频子带主要表征图像的近似信号。为了能够在增强图像的同时减少噪声的影响,可以对低频子带进行非线性图像增强,用以增强目标的对比度,抑制背景;而对高频部分进行小波去噪处理,减少噪声对图像的影响。然后提取各子图特征并归一化后作为卷积神经网络的输入进行进一步处理。 通过鸡蛋与苹果两个数据集实验测试表明,预训练的 CNN 模型能够提取出有效的图像纹理特征,在常用的纹理数据集上均取得较好效果。本文算法在数据预处理阶段利用了小波变换,CNN 训练主要体现在卷积层与子采样层的彼此交互。其中,各权值参数的最佳取值是影响卷积神经网络模型准确率的关键。后续工作将会针对特定领域的高相似图像进一步优化权值参数,提高算法在特定领域高相似图像识别与分类的准确性。
