无线传感网中分布式信号检测的多维特征值算法优化研究*

刘 云，陈 倩

(昆明理工大学信息工程与自动化学院，云南 昆明 650500)

1 引言

在大规模无线传感网的分布式信号检测中，由于测量信息量较大，容易造成数据收敛速度较慢、检测精度不高等问题[1]。利用数据集具有较高时空相关性和一定冗余度的特性，在减少信号样本数和迭代次数，保证较快收敛速度的前提下，最大程度提高检测精度是信号检测至关重要的问题。

文献[2]中，Zhou等人提出了一种基于协方差矩阵最大特征值的Cholesky分解算法MECD(Maximum Eigenvalue of Cholesky Decomposition algorithm)，该算法利用噪声功率的先验知识导出假警报概率和判定阈值的分析表达式，对噪声不确定性具有鲁棒性，但检测精度较低。文献[3]中，Tsinos等人提出了一种基于最大特征值的分布式子空间跟踪算法DST(Distributed Subspace Tracking algorithm)，该算法以完全分散的方式联合跟踪其接收信号的子空间，克服了集中方法的局限性，但在大型无线传感网中，其收敛速度较慢。

在研究MECD算法和DST算法的基础上，本文提出一种分散功率算法DPM(Decentralized Power Method)，用于分布式计算样本协方差矩阵的最大特征值，通过将平均共识和迭代功率法相结合，在相对少量样本和有限次数迭代的条件下，实现了协方差矩阵最大特征值的较快收敛速度和较高精度估计。对比MECD算法和DST算法，仿真结果表明，DPM算法在减少信号样本数和迭代次数，保证较快收敛速度的前提下，可以获得更高的精度。

2 模型建立

2.1 系统模型

考虑一个由K个传感器节点组成的无线传感网，在给定的时间间隔期间，每个节点收集N个复杂信号样本。全局接收采样矩阵表示为：

(1)

其中,y(·)∈CK和y[·]∈CN分别表示矩阵Y的列和行,C表示复数，列y(n),n=1,2,…,N,表示所有节点在时刻n时所接收的样本，行y[k]T,k=1,2,…,K,表示周期结束时在节点k处可用的所有样本。

样本协方差矩阵定义为：

(2)

在不失以递减排序的一般性下，令λ1≥…≥λK≥0为R的特征值，相应的特征向量为u1,…,uK。本文使用的符号如表1所示。

2.2 平均共识与功率法

(1)平均共识。

Table 1 List of symbols表1 符号列表

(3)

其中,z0[k]T表示在节点k处可用的样本，则在时刻t时AC函数的输出定义为：

11TZ0+Et

(4)

其中,1是大小为K的列向量，误差项为：

Et=[et(1),…,et(m)]∈CK×m

(5)

误差项Et假设是有界的或等于零的向量[7,8]。

(6)

(2)功率法。

功率法PM(Power Method)是一种迭代算法，给定方阵，收敛于与矩阵最大特征值相关联的特征向量[9]。样本协方差矩阵的迭代表示为：

v(j+1)=Rv(j)

(7)

(8)

3 DPM算法

3.1 定义

(9)

在式(7)中，向量v(j)的第k个元素表示为v(j)[k]，通过使用AC算法在节点k及其邻居节点之间迭代交换消息来实现。一旦元素v(j)[k]在节点k处可用，则再次采用AC算法来完成特征值计算所需的内积和范数，而在每个节点本地进行所有元素的操作(如求积、乘以常数等)[10]。对于功率法PM，需要以适合于AC的分散方式重写全局迭代，并将全局迭代分解为由各个节点执行的算法步骤的序列。

以下命题给出PM向量迭代的主要结果。

命题1给定理想的AC函数AC(·)，PM迭代重写为：

(10)

证明由式(7)可得：

(11)

(12)

结合式(11)与式(12)，可得到简化式(10)。

□

式(10)因具有以下属性而适合于分散实现：

(1)输出向量的第k个元素v(j+1)[k]是diag(YZH)第k个元素，因此：

v(j+1)[k]=z[k]Hy[k]

(13)

式(13)可以由节点k在本地计算所得，其中y[k]表示节点k的接收样本向量，z[k]表示节点k的AC输出。

(2)ACN(·)的输入是仅包含节点k本地数据v(j)[k]*·y[k]T的第k行。

假定DPM算法迭代v(j+1)已经重复了M次，则通过对AC函数进行两次附加调用来计算所有节点的最大特征值估计，如以下命题：

命题2给定理想的AC函数AC(·)，对v(j+1)进行M次迭代之后，可以通过下式获得最大特征值估计的K个本地副本：

1K=

(14)

其中,RN:CK×m→CK表示一个返回输入矩阵的行的平方l2规范的函数(见表1)。

证明首先在所有K个节点迭代M次之后，写出全局输出如下：

(15)

分子可以写为：

(16)

分母可以写为：

(17)

结合式(16)与式(17)，可得到简化式(14)。

□

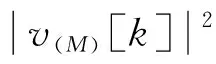
3.2 算法描述

根据命题1和命题2的结果，采用有限平均时间替代理想AC函数，则DPM算法代码如算法1所示。

算法1分散功率算法(DPM)

输入: 传感器k∈{1,…,K}的接收信号矢量y[k]∈CN；迭代次数M；初始值υ(0)[k]∀k；平均时间t。

for所有节点k同时do

for迭代次数j=1到Mdo

end

end

4 误差和复杂度分析

在本节中，针对非理想AC算法对DPM算法的误差和数值复杂度的影响进行分析。

4.1 误差分析

DPM算法涉及了由AC引起的三个误差源。第一个误差项定义为：

(18)

第二和第三误差项来自式(14)，被定义为：

(19)

(20)

4.2 复杂度分析

对于DPM算法，复杂性主要源于AC算法的重复使用，从而导致通信开销、时间延迟和可能的同步问题。在以下参数方面分析算法的复杂度：(1)调用函数的次数；(2)由一个节点通过无线信道交换的信息单元的总数，其中信息单元表示为用于编码标量的位的数目；(3)算法步骤的数量，由于输入、输出依赖性而必须以顺序方式执行单个任务。

为了对复杂度进行比较，考虑一个集中式多跳结构，其中每个节点将收集的样本发送到融合中心，且融合中心将结果转发到每个节点[12 - 14]。每个节点的最坏通信成本是2(K-1)N=O(KN)。对于DPM算法，通信成本为O(MNId)，其中，M表示DPM算法的迭代次数，N表示样本数量，I表示AC算法迭代次数，d表示节点数。因此，可以得出结论，当MId

5 仿真分析

5.1 参数分析

在减少信号样本数和迭代次数，保证较快收敛速度的前提下，为了获得较高的检测精度，需对本文算法的仿真参数进行设定。假设一个分布式信号检测场景，其中多个传感器节点协作以检测主要信号的存在，每个传感器基于接收信号样本做出关于信号存在或不存在的判定[15,16]。从数学角度，将问题转换为二元假设检验，即“信号加噪声假设(H1)”和“仅噪声假设(H0)”，且在整个感测期间所有传感器具有相同的假设[17,18]。当假设为H0时，传感器K在给定时刻n的接收信号矢量为：

y(n)|H0=η(n)

(21)

其中η(n)～(0,δ2I)。

当假设为H1时，接收信号矢量为：

y(n)|H1=Hs(n)+η(n)

(22)

为了对所提算法进行数值评估，考虑一个由K=40个节点随机生成的无线传感网络。假设一个信号加噪声模型(H1)，在每个蒙特卡罗迭代中随机生成接收信号样本Y。仿真具有以下参数：每个节点具有N=10个样本，噪声方差δ2=1，具有SNR(ρ=5 dB)的一个高斯信号源(P=1)。

5.2 仿真分析

(1)收敛速度分析。

如图1所示，随着迭代次数的增加，DPM算法、MECD算法和DST算法的均方误差逐渐减小。当迭代次数M=1时，DPM算法、MECD算法和DST算法的均方误差分别为：0.63 dB，1.2 dB和1.42 dB。当迭代次数M=12时，DPM算法、MECD算法和DST算法的均方误差趋于平缓。对比DST算法和MECD算法，DPM算法的收敛速度最快。

Figure 1 Diagram of the mean square error versus the number of iterations图1 均方误差随迭代次数的变化

(2)精度分析。

Figure 2 Diagram of mean square error versus time图2 均方误差随时间的变化

(3)检测率随虚警率变化分析。

如图3所示，随着虚警率的增加，DPM算法、DST算法和MECD算法的检测率逐渐升高。当虚警率为0.05时，DPM算法、DST算法和MECD算法的检测率分别为0.79、0.72和0.69。当虚警率为0.5时，DPM算法、DST算法和MECD算法的检测率分别为0.996、0.97和0.918。对比DST算法和MECD算法，DPM算法的检测率较高。

Figure 3 Diagram of detection rate changing with the false alarm rate 图3 检测率随虚警率的变化

(4)检测率随信噪比变化分析。

图4显示了检测率随信噪比的变化情况。从图中可以看出：随着信噪比的增加，DPM算法、DST算法和MECD算法的检测率逐渐升高。当信噪比较低时(SNR=-9 dB)，DST算法的检测率比MECD算法增加28.5%，DPM算法的检测率比DST算法增加27.8%。对比DST算法和MECD算法，DPM算法具有更高的噪声鲁棒性。

Figure 4 Diagram of the detection rate changing with the signal to noise ratio 图4 检测率随信噪比的变化

6 结束语

在大规模无线传感网的分布式信号检测中，针对相关性较高并有一定冗余度的数据集，为解决传输数据量大引起的收敛速度慢、估计精度低等问题，本文提出了一种分布式计算样本协方差矩阵最大特征值的分散功率算法(DPM)，通过将平均共识和迭代功率法相结合，在少量样本和有限次数迭代的条件下，实现了最大特征值的较快收敛速度和较高精度估计。对比MECD算法和DST算法，仿真结果表明，DPM算法在减少信号样本数和迭代次数，保证较快收敛速度的前提下，可以获得更高的精度。