转换思想在高中数学解题中的应用

江苏省如东高级中学 吴 晔

数学学习不仅帮助学生们掌握一些基础的知识点，还能帮助学生们学习到一些数学的解题思想，数学思想是在解决数学题目时对解题规律、数学知识点的一些抽象的概括，在数学学习中，常常能帮助学生们快速捕捉到解题的重点并且快速解题。转换思想就是其中一个比较重要的思想，它是将问题中一些陌生的、未知的、复杂的条件转换成其他形式，使其变得更加简单、明白、容易理解，方便学生们进行解题。数学的转换形式是多样的，可以由文字转换为图形，符号转换为文字等，它们之间的转换是自由的，是可逆的。

一、在高中数学解题中转换思想的作用

1．帮助高中生们提高思维的严谨性

高中是学习的重要阶段，在这个阶段，学生们会接触更多的知识，而且知识点比较多，也相对复杂，所以这个时期是他们养成良好思维并不断发展的重要时期。通过在高中对数学繁多内容的学习，大量的习题练习，能够帮助学生们养成并锻炼思维能力。在数学解题中，思维的严谨性是十分重要的，随着高中数学教学的不断开展，学生们学到的知识越来越多，在数学习题中涉及的知识点就会越来越多，也越来越复杂，这时就对学生们思维的严谨性提出了很高的要求，要求考虑清楚题目当中都涉及哪些知识点，并且该怎么运用，思维的严谨性就要求弄清楚每一个点，帮助学生们提高解题的正确性，而在解题中适当运用转换思想时，刚开始是有点复杂困难的，但学生在不断思考和不断地尝试转化当中，就会自觉提高他们自身思维的严谨性了。

2．帮助高中生们养成良好的解题习惯

有一些学生，他们本来对于老师讲述的知识点都能牢牢记住，但是在解题时却不会应用，或者是总是不能正确地把题目解答出来，其实都是因为这些学生的解题习惯不好，导致一而再再而三地做错，还有时是将原来做过的题目的一些条件略微进行一些调整，许多学生就不会做了，这都是因为学生们在解题时审题不严谨，比较粗心，没有仔细分析题目，看漏看掉条件，所以总会出现一些小错误。老师在教学过程中要对学生进行反复训练，使学生们克服那些缺点，养成在应用转换思想解题时全面思考的习惯，慢慢地，学生们就会养成良好的解题习惯，提高做题的效率和准确性，帮助他们在数学方面的学习。

二、在高中数学解题中转换思维的应用

在高中学习之中，应用转换思维解题是很常见的，但是它还存在着许多问题，为了学生们能充分掌握这种方法并且熟练应用，老师要优化自己的教学，找到不同学生的不同特征，对自己的教学进行优化，不断创新，帮助学生们快速、轻松地发展与进步。

1．在导数解题中的转换思维

在导数的学习中，有些问题可以借助函数来进行解答，这些问题大多题干简单，包含信息较多，解题复杂，所以当许多学生碰到这类问题时，常常不想思考，选择放弃，但是其实只要找到问题的关键就很好解答了。转换思维很好地帮助我们将文字性题目转化为图形，化无为有，通过这种数形结合，使得学生们的解题变得更加容易。

例如，在学习了函数的零点时，有题：已知一个函数f（x）=x-[x],[x]表示不超过实数x的最大整数，现有一函数g（x）=f（x）-kx-k有4个零点，求实数k的取值范围。

这个题目刚看就会发现题干中的已知很少，只有两个函数表达式以及有一个函数有四个零点，直接计算对于学生们来说是十分困难的，于是学生们可以借助图形的方式来解题。已知f（x）=x-[x]，再令h（x）=k（x+1）,这样就将g（x）拆成了两个函数，画出两个函数的图象如下：

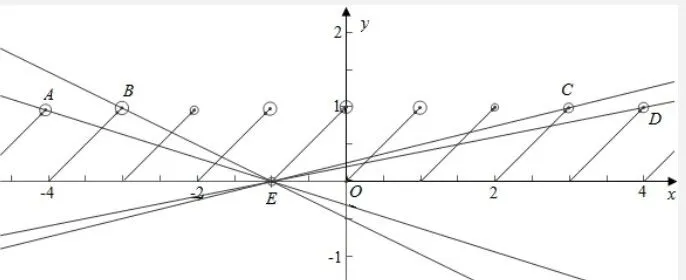
从图象可以看出，函数f（x）的图象是规律的，最上面的点是一个虚点，而g（x）是一个绕点（-1，0）旋转的直线，因为g（x）有三个不同实根，因此，函数f（x）与g（x）有三个交点，只要求出有三个交点时g（x）的斜率就可得出结论。由图可知，在y轴右边，当直线在点（2，1）和点（3，1）之间时是有三个交点的，此时直线的斜率分别为当在y轴左边时，当直线在点（-2，1）和（-3，1）之间时有三个交点，此时的斜率分别为k=-1将这些答案进行整合，就可以得出最后结果为

这个题目的关键就是将文字性的表达转换成函数图形，通过图象就可以直观地看出答案了，一开始直接解题也许会很难，但是多尝试转换思维，解题就会变得容易多了。

2．在三角形解题中的转换思维

在学习三角形时，随着学习的不断深入，我们会从认识三角形到等腰、直角、等边三角形以及三角形的边长和面积的求解，到了高中，更加深入地学习了三角函数的内容，在许多解题中给了学生们很大的帮助。例如：有一个三角形ABC的三个内角对应的边长为a、b、c，且满足则三角形ABC周长的最小值是多少？

这个题目要求的是三角形周长的最小值，于是轻易想到可以将这个题目转换为求一个不等式的题目，这样就可以求出a+b+c的最小值。但是题目却没有给出一条边的长度，已知条件也只有两个，一个是边的关系，一个是角的大小，于是就可将角的大小转换成边的关系，然后根据这两个边的条件找出各个边之间的关系，根据（a+b）2-c2=4得a2+b2+2ab-c2=4,根据化简得由不等式可知当且仅当时等号成立，再由所以周长

刚解题时也许会觉得有些困难，但是通过学着转换思维的慢慢运用，题目慢慢就会转换得清晰、简单，做题就方便多了。

其实，转换思维在数学的很多方面都有运用，例如在有关向量的题目当中，有时弄不清长度、方向之间的关系，就可以通过画坐标轴的方式，标出每一点的坐标，将向量之间的关系变成坐标点之间的关系，有时就能方便学生们解题了。在圆锥、椭圆等题目当中，也可以通过转换思维的方式来解题，可以将左右焦点的坐标和距离等进行转换，得到题目没有给出的条件。所以，在数学学习中，转换思维是一个十分重要的思维，只要学生们了解并且掌握了这种思维，就可以慢慢对题目进行深入分析，找准转换对象，找对转换方向，合理分析，将题目转换为方便自己计算的形式，这样就可以将原本很难的数学题慢慢击破，慢慢提高数学解题能力，自然而然，学生们的数学成绩也会不断提升了。