带锯机架整体的筋板结构设计与优化
2018-09-28如翔
,,如翔, ,
(南京理工大学机械工程学院,江苏 南京 210094)
0 引言
木工带锯机床是一种历史较长,使用最广的木工加工机械。其优点突出,主要包括可以锯切大径级及以上的原木;锯屑损失相比圆锯机与框锯机减少都在1/3以上[1]。然而,现阶段大多数木工带锯机床也存在着普遍缺点,如机床振动严重,锯切质量不高等[2-4]。其主要原因是木工带锯机架大都是焊接件,且焊接精度不高,导致上下锯轮不平行,强度不高。若采用机架铸件,则可以提高机床的整体性能,增强其结构刚度。但是铸件整体质量较大,不利于运输,所以对机架铸件的质量、筋板结构及强度进行优化设计,对木工带锯机床的整体优化具有至关重要的作用。
1 机架的整体结构模型
机架是木工带锯机床的主要承重部件,各工作部件都以机架为基准设计与安装,如图1所示。图1中,机架为铸件,下方为箱型结构,上方为伸出梁结构,右侧为立柱。相比于现阶段的焊接机架,该机架整体强度高,不易使带锯条在锯切过程中产生径向跳动[5-7],从而有助于减小机床振动,提高锯切精度。

图1 带锯机内部结构
2 筋板结构单元类型与特征
由于机架下方需承受下锯轮、电机等的质量,所以在实际的设计过程中,需布置相应的加强筋板以提高机架下方的结构强度。而机架其他部分,如右侧立柱、上方伸出梁部分也可以采用加强筋结构来降低机架的质量。
壁板类单元是一种附着于壁板上重复排列的可看成有一定高度的二维形状的筋板组合[8]。采用壁板类单元,可以在增强机构件强度的同时,减轻机床质量。
2.1 筋板单元动态性能分析
2.1.1 动态性能分析原理
对筋板单元的动态性能进行分析,建立反映振动系统的动力学模型和数学模型。根据数学模型,求解系统主振型和固有频率的初始特征值。
对于一个自由度不定的线性系统,其运动微分方程[9-10]为:
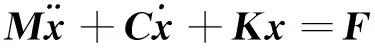
(1)
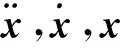
当F=0时,可将方程转化系统无阻尼的自由振动方程:
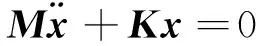
(2)
又因线性振动位移函数为简谐振动函数,其解的一般形式为:
x=Hem(m=iω0t且i2=-1)
(3)
由线性代数可知,系数行列式需满足:
(4)
H为系统振幅矩阵;ω0为固有频率特征值,其中ω01,ω02,…,ω0n所对应的振幅矩阵依次为H1,H2,…,Hn。将
代入方程中,得到n个相应方程,形式为:
(5)
r=1,2,3,…,n
得出固有频率的特征值ωq,以及其对应的振幅矩阵:
(6)
建立符合筋板单元振动系统的数学模型,不仅证明了固有频率和主振型振幅是系统固有属性,而且进一步推导出系统内部固有频率与主振型振幅的变化关系。
2.1.2 4种筋板的动态性能比较
基于动态性能分析原理,将4种筋板结构单元进行参数化建模。其中,筋板宽度L=5mm,厚度H=10mm,材料为结构钢。在保证其受载荷面面积相同的情况下,对各固定接触面进行约束,运用模态分析对其固有频率进行计算。
4种筋板的前6阶频率如表1所示。
井字形筋板单元经计算后的一阶固有频率如图2所示;米字形筋板单元经计算后的一阶固有频率如图3所示;X字形筋板单元经计算后的一阶固有频率如图4所示;T字形筋板单元经计算后的一阶固有频率如图5所示。

表1 4种筋板单元频率 Hz
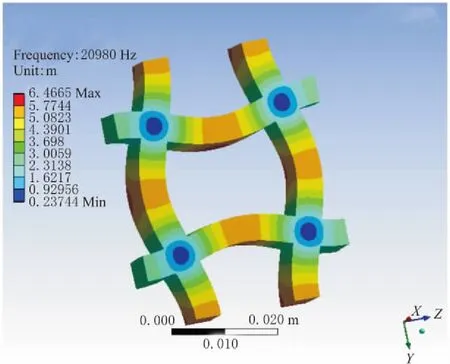
图2 井字形

图3 米字形
一阶振型反映结构在平面内绕结点扭转时的模态,为结构薄弱模态;二阶振型反映结构沿Z方向水平位移时的模态。一阶和二阶振型为筋板结构在运动中的主要振型,在筋板结构选型时为主要参考依据。由表1可知,井字形筋板结构的一阶固有频率为20 980Hz,二阶固有频率为26 216Hz。而T字形筋板结构的一阶固有频率为17 367Hz,二阶固有频率为31 053Hz,均高于其他2种筋板单元。

图4 X字形

图5 T字形
2.2 筋板结构单元动态载荷分析
对上述4种筋板结构单元进行有限元变形分析,根据筋板在机架中的实际受力情况,分别对筋板受载荷面施加200Pa,300Pa,400Pa的垂直于受载荷面的均匀压强。其中,筋板宽度L=5mm,厚度H=10mm。不同筋板结构单元的整体变形随压强变化如表2所示。

经筋板结构动态性能和载荷分析得出,井字形和T字形筋板在受扭转和平面载荷时,主振型固有频率较高,且变形较小。结合机架整体受力情况可知,机架上端伸出梁部分主要受垂直方向的挤压变形,宜采用T字形筋板。而机架下方箱体结构部分受平面压力为主,宜采用井字形筋板。
3 机架有限元分析模型
建立带锯机床铸件机架的三维模型,并将机架模型参数化[11]。 模型建立时,不仅要考虑模型与实际零部件紧密结合,还要考虑模型计算的可行性[12-14],省略原模型中的部分小孔、倒角和圆角等对整体机架力学性能分析结果影响较小的几何特征。
将参数化模型连接导入ANSYS软件中,根据机架的结构设计形状和受载荷分布特点,选择自由网格划分,选取网格的尺寸为5mm,机架网格划分结果如图6所示。
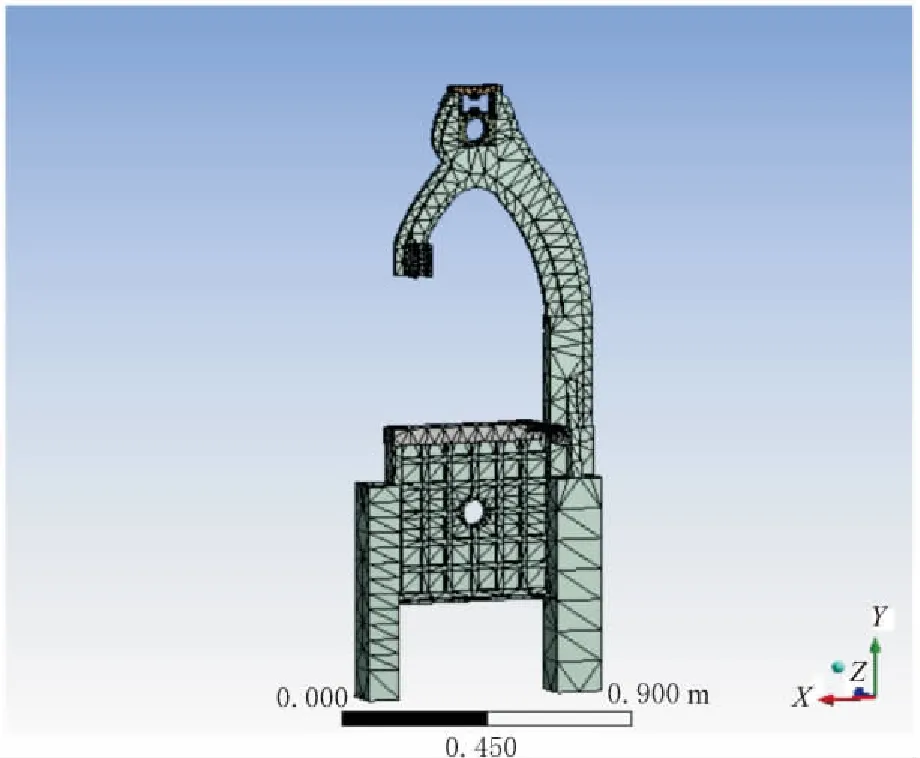
图6 机架有限元模型
4 静态应力分析
4.1 载荷及约束处理
4.1.1 载荷处理
木工带锯机架为承载式机架,机架的本体质量通过设置材料密度属性自动添加,而其所受的外部载荷如上锯轮质量、下锯轮质量、工作台质量和带锯锯卡质量等,通过等效简化为集中载荷,加载到相应的承载部位。
4.1.2 工况约束处理
工况为匀速锯切状态。对机架顶端张紧滑块添加约束,约束其4个自由度,保留其垂直于地面方向(Z轴)的平移自由度。对机架底部添加固定约束,约束其所有自由度。
4.2 结构模型的有限元分析
在匀速锯切状态下对机架模型进行有有限元分析,由于机架为灰铸铁铸件(材料HT200的抗压强度σbc=200MPa,抗拉强度Rm=60MPa),其抗拉强度与抗压强度相差较大,所以需对机架所受力进行区分,判别其力学属性。
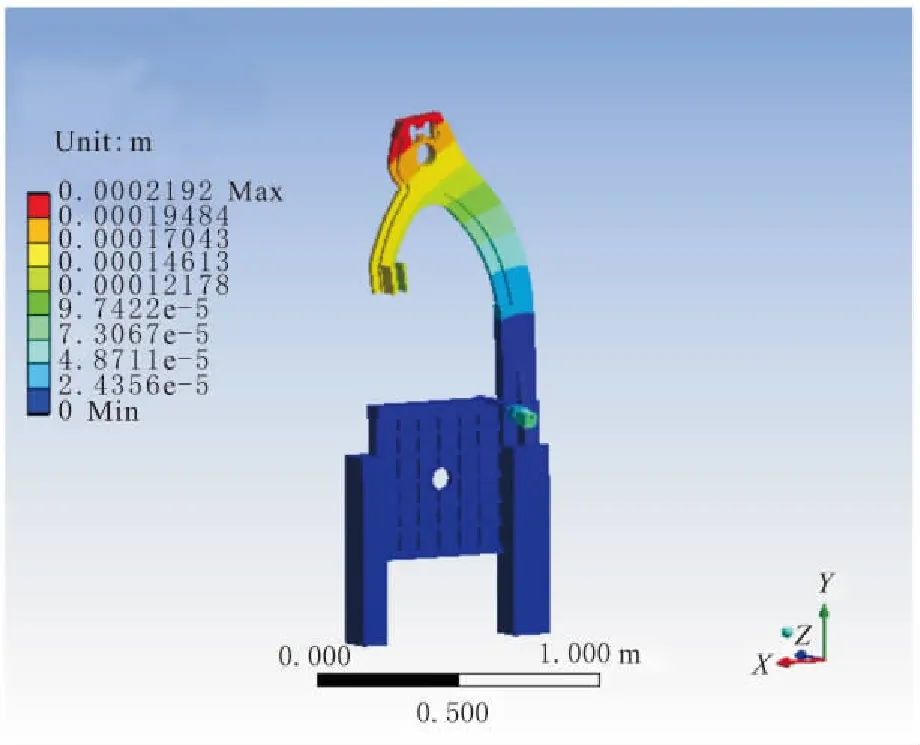
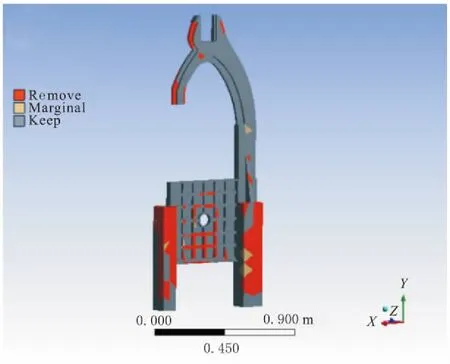
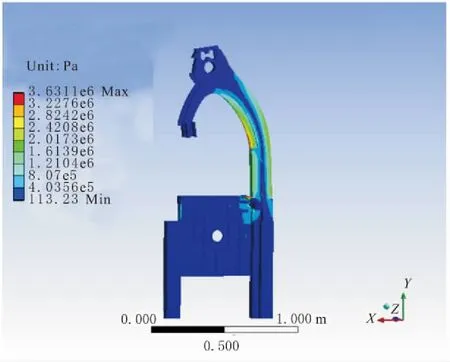
分析得出,机架最大等效应力位于机架伸出梁内侧,该位置所受力表现为压力,最大等效应力σmax=4.027MPa≪σbc。而伸出梁外侧所受力表现为拉力,该位置最大的等效应力σmax=2.685MPa 图7 机架锯切应力 图8 机架锯切应变 为降低木工带锯机架质量在整机质量中的比例,由静力学分析结果发现,该机架在匀速锯切工况下所受的应力较小,在满足机架强度要求下,仍存在较大的设计余量[15-17]。基于上述有限元分析结果,采用结构拓扑优化对该木工带锯机架铸件进行整体轻量化设计。 5.1.1 数学模型 拓扑优化的基本思想是在给定的设计区域内,把寻找结构最优的问题转化为寻找材料分布最优的问题,常用的方法是变密度法[18]。而基于ANSYS的拓扑优化目标函数是在满足结构约束的基础上,使结构整体的柔度最小,等效于结构强度最大。约束函数是在已给定最小形变和载荷下缩减体积的百分比。 其拓扑优化数学模型如下所述。 目标函数: minV(x)=V(x1,x2,…,xn) (7) 约束条件: (8) 其中,x=(x1,x2,…,xn)为设计变量;V(x)为目标函数;g(x)为不等式约束函数;h(x)为等式约束函数;xmin表示下限取值;xmax表示上限取值。 5.1.2 优化过程 a.将机架有限元模型导入ANSYS Workbench软件中,根据该机床锯切工况,设置各结构模块材料属性、载荷和约束,设置结束后,对模型进行静力求解。 b.将静力学求解验证的机架导入shape optimization模块中,根据该木工带锯机的减重需求,将优化目标参数定义为减重20%,得出的拓扑优化结果如图9所示。其中,理论可去除部分为红色区域(颜色较深),建议保留部分为灰色区域(颜色较浅)。 c.依据拓扑优化结果和实际工况要求对该机床机架进行结构优化,并对尺寸修改后的模型进行静力学分析,修改后应力分布如图10所示。 图9 机架拓扑优化图 由图10可知,拓扑优化后机床锯切工况下最大等效应力σmax=3.631 MPa,由于拓扑优化去除机架不必要体积,相比优化前,最大等效应力也有所下降,强度得到明显提高。该机架通过质量拓扑优化,整体质量由226.379 kg减少到188.150 kg,质量减少了38.229 kg,实现了机架整体轻量化设计。 图10 机架轻量化后模型 根据运动微分方程,建立适合筋板结构系统的振动分析模型,进一步推导出系统内部固有频率与主振型振幅的变化关系。 根据筋板结构动态性能分析结果,比较4种筋板结构的各阶固有频率,得出最适宜筋板结构模型。 根据动态载荷分析,得出井字形筋板单元和T字形筋板为该最适合该机架的筋板单元类型,且实际强度与刚度均符合设计要求。 根据拓扑优化分析结果,对木工带锯机床机架进行轻量化设计,使机架整体质量降低了16.9%,实现了轻量化目标。 根据轻量化分析结果,对该木工带锯机架进行了合理的结构改进,降低了机床最大应力,提高了整体结构刚度。 木工带锯机床机架的轻量化设计与优化,对于相关林业机械的设计和研发具备一定的参考价值。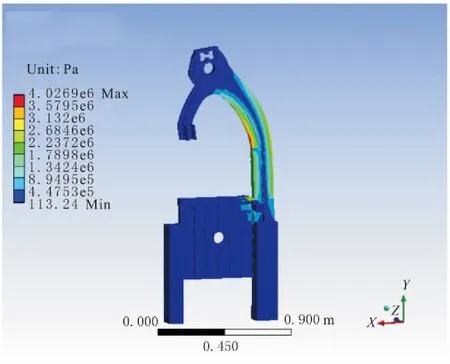
5 轻量化设计
5.1 拓扑优化
6 结束语
