基于聚类分区算法的FPGA高效动态部分可重构设计*
2018-09-27宋林峰董宜平
谢 达,宋林峰,董宜平,胡 凯
(中国电子科技集团公司第五十八研究所,江苏 无锡 214072)
1 引言
目前,可重构系统已经被广泛运用于复杂应用之中,在提高应用性能的同时降低了应用成本。现场可编辑门阵列(FPGA)因其具有高性能和高灵活性的特点,成为实现可重构系统合适的硬件平台。当前最新的动态部分可重构(Dynamic Partial Reconfiguration,DPR)技术可以使FPGA在重新配置一部分电路的同时允许其余部分保持正常运行,进而提供了更高的灵活性。
DPR系统由许多可重构模块(Reconfigurable Modules,RMs)组成,每个RM具有不同的功能模式。这些RMs可以在动态重配置系统的控制下在运行中进行变化。RMs物理上由部分可重构区域(Reconfigurable Regions,RRs)定义在 FPGA 的一些特别位置上,使得整个系统的可重构部分与静态部分分离。分区是根据RMs的功能模式种类数来确定RRs数量和大小的过程。其中,重配置时间(即重新配置系统由一种工作模式转变到另一个工作模式的时间)与RRs的面积大小成正比。因此,重配置时间和可重构区域面积是衡量一个DPR系统是否高效的重要指标。
DPR设计方案的核心是给动态可重构模块分区。为了实现最短时间和最小面积,研究人员在DPR分区方面已经开展了一些相关研究工作。Berrocal[1]等提出一种动态时间的时间分区方案以减少重构时间,在重配置期间启用时域分区来重新连接可重新配置的分区区域,从而实现了模块间互联,但没有考虑可重构区域面积。Montone[2]等提出了一种模拟退火算法来最小化可重构区域面积,但没有考虑可重构时间。Vipin[3]等指出两种最常用的DPR分区方法,单区域划分法和模块化分区法,但这两种方法都只优化了重配置时间和可重构区域面积的其中一方面。Vipin[4]等基于改进的层次聚类算法提出了一种自动化的分区工具,该工具能够找到最小重构时间的最优分区方案,但没有对可重构区域的面积进行优化。Yousuf[5]等提出了一种软硬件综合设计的自动化分区流程,将RM s分配到FPGA的可重构区域,但只针对特定应用提高了重构时间和应用频率。因此,自动化分区成为DPR设计的趋势,而同时优化配置时间和区域面积仍然是设计的难点。
针对现有研究的趋势和难点,本文提出了一种高效DPR设计方案,改进了Vipin分区算法[4],得到最优分区方案,可以同时减少整个DPR系统的重配置时间和总面积,此外还设计了一个重配置布线开关;在系统运行时重新连接RRs,解决了RRs之间静态布线的问题;最后基于Xilinx的Kintex-7系列FPGA进行了实验和分析。
2 动态部分可重构的现有研究基础
2.1 DPR基本原理
可重构是一种在硬件结构可变的基础上对电路进行重配置的概念。FPGA实现可重构的基础是静态存储器(SRAM)结构,基于此原理的FPGA可以实现可重构,支持动态可重构的FPGA。如Virtex系列器件的物理结构由输入输出模块(IOBs)、Block RAM、配置逻辑块(CLBs)等部分构成。SRAM配置层也根据这些模块进行了划分,最小单元为配置列(Configuration Columns)[6]。如图1所示,下载到SRAM的配置数据流分成配置数据和配置地址两部分,地址指向不同的配置列。当FPGA进行配置时,配置存储器根据下载数据中的地址信息寻找对应的配置列,然后将该配置列对应的配置信息(Frames)下载进去。因此,当仅下载部分配置列的数据和地址时即实现了动态部分可重构配置。
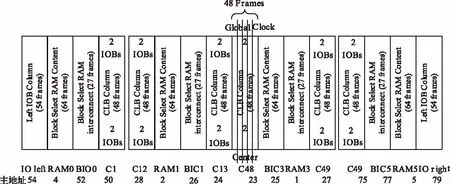
图1 具有DPR功能的FPGA配置存储器结构
2.2 现有DPR设计方案
迄今为止主要有4种DPR系统实现方案,分别为基于JBits的设计方案[7]、基于差异的设计方案[8]、基于模块的设计方案[9]以及基于EAPR(Early-Access Partial Reconfiguration)流程的设计方案[10]。前两种方案因需要手动进行布局布线,复杂应用使用起来难度较大。Xilinx公司近几年提出了基于EAPR的设计方案,此方案继承了基于模块设计方案的优点,并进行了一系列改进,如改变模块的基于TBUF总线宏为基于Slice的总线宏,使总线密度更高、通信质量更好;可重构区域也从有限制的矩形变为任意矩形等。因此目前应用最多的设计方案为基于EAPR的方案。
本文提出的DPR设计方案采用的是基于EAPR流程的设计方案,具体流程如下:顶层模块设计、静态模块设计、重构模块设计、总线宏设计以及模块合并。设计一个动态部分可重构系统的流程图如图2所示。
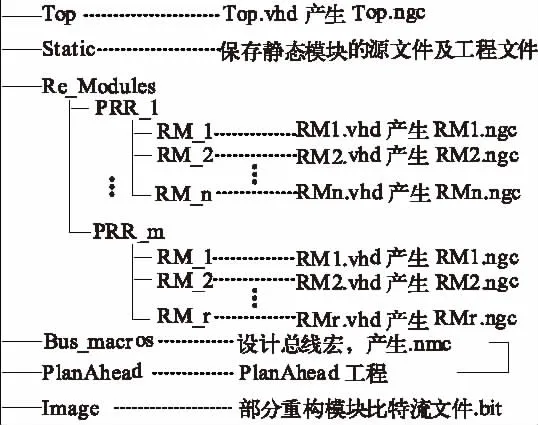
图2 基于EAPR的设计流程
设计出的部分动态可重构系统的基本结构框图如图3所示。部分可重构系统物理上由静态区域和动态区域构成,RMs定义在动态区域中,RMs的数量根据应用需要的功能模式种类数决定。静态区域和动态区域通过总线宏(Bus Macro)连接,设计时三者的关系都定义在顶层模块中,从而建立静态区域和动态区域的连接。
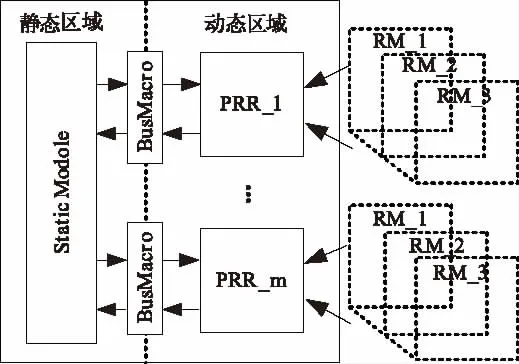
图3 DPR系统的基本结构框图
2.3 现有DPR分区方案
DPR系统是由多种配置模式(Configuration Modes,CMs)组成,每种 CM 包括多个 RM s,在系统工作时,可重构模块会从一种配置模式转变成另一种配置模式。以一个DPR系统为例,如图4所示,该系统有4 种配置模式(Conf.1,Conf.2,Conf.3,Conf.4),每种配置模式有4个 RMs(A,B,C,D),每个RM有3种模式(A1,A2,A3;B1,B2,B3;C1,C2,C3;D1,D2,D3)。
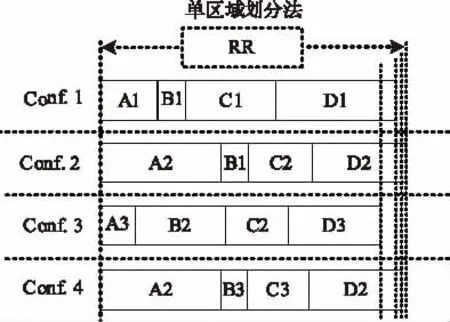
图4 常用DPR分区方案之单区域划分法
目前实际最常用的分区方案有两种[3]:第一种是单区域划分法,如图4所示,此方法是将所有RM s分区在一个大尺寸的RR中,这个区域包括最大配置模式(图4中为Conf.2)所需要的资源;第二种是模块化分区法,即每个RR分区放置一个RM,如图5中RM_A放置在RR1分区,RM_B放置在RR2分区,这样在系统运行时,每个RR将从一种可重构模式转换成另一种。同时,每个RR要包含其区域内的RM在每种配置模式中用到的资源,如图5中RR1要包含RM_A 的 3种模式(A1、A2、A3)用到的资源。
Ki-67属于一种抗原,主要针对细胞增殖周期,其主要存在于细胞核中,通常在细胞生长的时期,并对细胞增殖进行控制,AM疾病患者中,其腺上皮水平的表现主要呈现为升高趋势,这就会使患者异位的病灶产生极强的增殖活性,并能促使AM疾病的发展[19]。
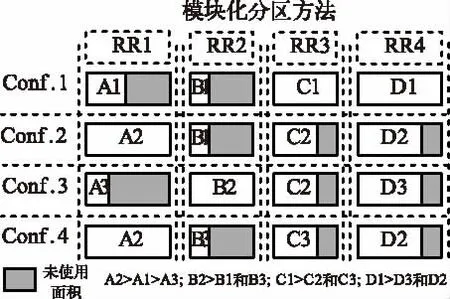
图5 常用DPR设计分区方案之模块化分区法
方案一需要较长的固定配置时间,因为从一种配置模式(conf.1)切换到另一种配置模式(conf.2)时,需要整个也是唯一一个可重构区域进行重配置,所以重配置时间很长。但此方法在面积上有优势,因为此方案可重构面积为最大配置模式所需的面积,这是能够实现所需功能的最小面积。对于方案二,RRs的数量等于RMs的数量,且每个RR的大小等于分配在这个区域上最大RM模式的大小,如图5中4个可重构区域的大小分别为(RR1:A2;RR2:B2;RR3:C1;RR4:D1)。这种方法的配置时间小于方案一,因为当系统从一种配置模式转换成另一种时,只需要一些RRs重配置,而不需要整个系统所有可重构区域重配置。但从面积上来讲此方案效率较低,因为整个可重构面积等于所有RM最大模式面积的和,如图5中整个面积等于A2、B2、C1和D1面积的和。且此方案在配置时有很多未使用的面积,也降低了配置效率。
3 本文提出的动态部分可重构设计方案
3.1 本文提出的分区方案
本文提出了一种分区方案,利用分区算法为给定的DPR系统找到最优的RRs大小和数量设置,如图6所示,按照每种配置模式中可重构模块的大小进行分区 , 如 Conf.1 中 B1<A1<C1<D1, 依 次 分 区 为RR1<RR2<RR3<RR4,Conf.2/3/4 同理。这样,每个可重构区域就包含了不同的可重构模块的一些模式,如RR1包含A3、B1和B3。同时,配置顺序还是原来的顺序,如Conf.1中从RR1的B1连接到RR3的C1,若切换到Conf.2则从RR1的B1连接到RR2的C2。因此需要一个布线开关处理重配置时RRs之间重新连接的问题,布线开关作为一个定制的可重构IP核置于静态区域。这种方案还可以将同一种配置模式中相同设计的RM合并到一个RR中以进一步减少面积,如A1和B1。最终配置时未使用的面积大大减少,因此该方案在配置时间较少的同时可以降低总重构面积。
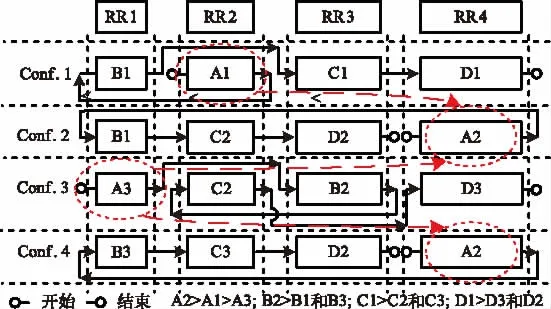
图6 本文提出的DPR设计分区方案
3.2 本文提出的分区算法
本文引用了Vipin分区算法[4],该算法通过一个图形网表实现DPR自动分区,其中节点权重是配置模式中所有模式发生的次数,边缘权重是两个模式同时发生的次数。本文提出的算法在其基础上作了改进,具体步骤如下。
第一步,算法遍历整个图形网表来生成一个包括所有可能分区的基本分区设置,该设置包含单个RM和可以合并的RM分区,可以合并的分区是指设计兼容、使用的基本单元兼容,例如图6中{(A1);(C2);(A1,B1);(B2,C2);(A2,C3)}。
第二步,从这些基本分区方案中选择一个候选分区方案,选择候选分区的依据是:选择的分区包含所有配置模式中所有的RM模式。Vipin算法的候选分区还要求排除所有包含可以合并但非连续RM模式的基本分区。例如图6中,(A2,C3)是可以合并的非连续RM模式。而本文提出算法的候选分区包含可以合并但非连续的分区。
第三步,从候选分区方案中搜索可以兼容的分区方案。可以兼容的分区是指两个或多个候选分区的RM模式不同时出现在任何配置模式中,因为在一种配置模式下,同一个RM模式不能重复出现。
最后一步,算法遍历所有可兼容的分区方案,以最小总重构时间为目标找出最优解决方案。
本文提出的分区算法在候选分区中包含了可以合并的非连续RM模式,因此相比Vipin分区算法,本文提出的分区算法可以得到更优化的分区方案,从而同时减小区域面积和重配置时间。
3.3 本文提出的分区布线技术
本文提出的分区算法对可重构区域之间的布线通信也进行了改进,因为本文提出的分区算法在候选分区中包含可以合并的非连续RM模式,所以最终得到的最优分区会由不同RMs的不同模式共享同一个RR,如图6所示,因此需要一种重布线技术来保证系统数据流的传递。图7所示为本文提出的布线开关。布线开关是由静态区域中的多路复用器和解码器实现的。开关的输入端口连接到所有RR的输出端,开关的输出端连接到所有RR的输入端。设计一个有限状态机(Finite State Machine,FSM)给开关发送控制信号来控制走线,在系统重配置时改变输入和输出端口的连接,实现RRs之间的切换。布线开关包含DPR系统中每一种配置模式的所有RM模式的布线映射。
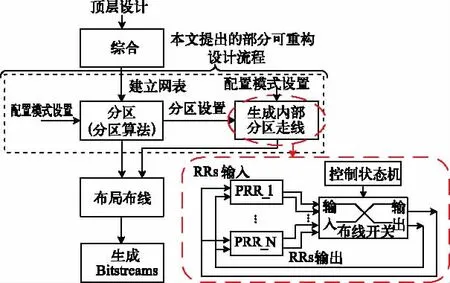
图7 本文提出的DPR设计流程与内部分区走线流程
4 基于KC705平台的实验结果与分析

图8 本文使用的KC705平台
软件开发环境为Vivado 2017.2。这里对比测试了4种分区方案,分别是(1)常用方案一(单区域划分)[3];(2)常用方案二(模块化分区)[3];(3)Vipin 分区算法[4];(4)本文提出的分区方案。对比使用这4种分区方案设计的16个DPR用例在可重构区域面积和重配置时间上的效果。
以一个4种配置模式的应用为例,单分区方案即一个区域;按模块化分区方案需要4个RR分区;Vipin分区方案需要3个RR分区;根据本文提出的设计方案只需2个分区,因为根据本文提出的分区算法,其中一些非连续的RM可以合并在一个RR区域。具体分区如图9所示。
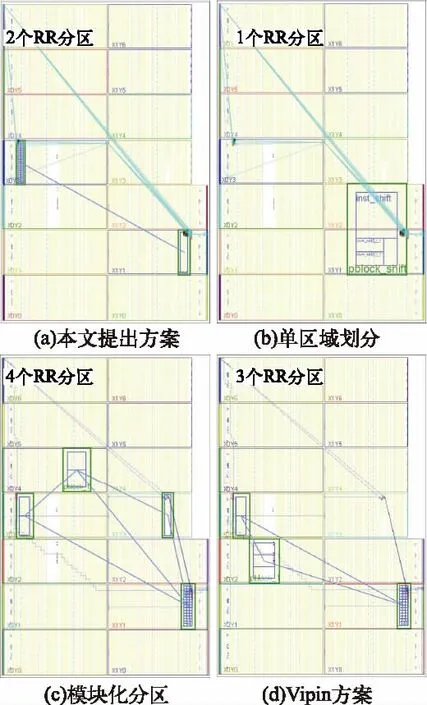
图9 4种DPR分区方案分区
本文提出的动态部分可重构设计方案中还增加了布线开关,即在不同的配置模式下,RR之间的连线通过布线开关进行变换,生成新的走线,如图10所示,其中(a)为常用方案与Vipin算法方案的静态走线,只有固定走线;(b)为本文提出的方案走线,虚线中为固定布线,实线中为分区布线的新走线。
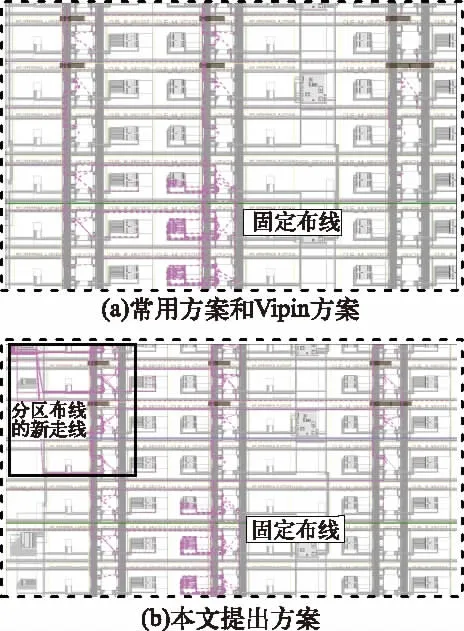
图10 4种DPR设计内部分区走线
本文采用了16个动态部分可重构设计用例来测试本文提出的设计方案。这些设计用例由简到繁,如表1所示。

表1 16个动态部分可重构设计用例
整个配置时间的计算公式见式(1)[4]:
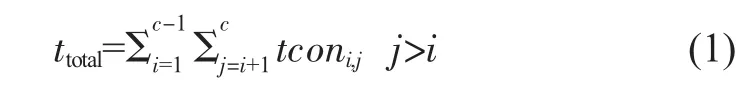
其中c是配置模式的总数,tconi,j是系统从模式i改变到模式j所需的重配置时间,tconi,j计算方法见式(2):
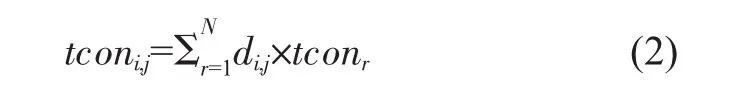
其中di,j是一个变量,当区域RRr在模式i和模式j下包含不同的RM模式时,di,j为1;否则为0。N是分区总数。tconr为配置区域RRr的时间,和该区域的面积成正比,区域面积Pr可以通过配置该区域所需的数据帧数表示,其计算公式见式(3):

其中 t指单元种类,t∈(CLBs,DSP,Block RAMs),Wt是一个单元所需的配置帧数。Wclb=36,Wdsp=28,Wbr=30。Rrt是该区域包含t单元的个数。
所以总的配置时间为:
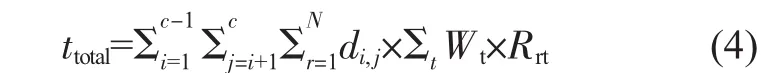
总的可重构区域面积为所有分区的面积之和,计算公式见式(5):

这里 Qr是区域 RRr中 CLBs、DSP、Block RAMs的数量,N是RRs的总数。
以4种配置模式4个RMs的应用为例,配置模式与图6相同,配置变化如下:
A1→B1→C1→D1
A2→B1→C2→D2
A3→B2→C2→D3
A2→B3→C3→D2

表2 4种配置模式4种RMs的用例分区情况
根据每种方案的分区情况,如表2所示,统计出每个区域包含的CLBs、DSP、Block RAMs的数量,根据式(4)计算出CLBs等单元所需的帧数,即总重配置时间,见表3。
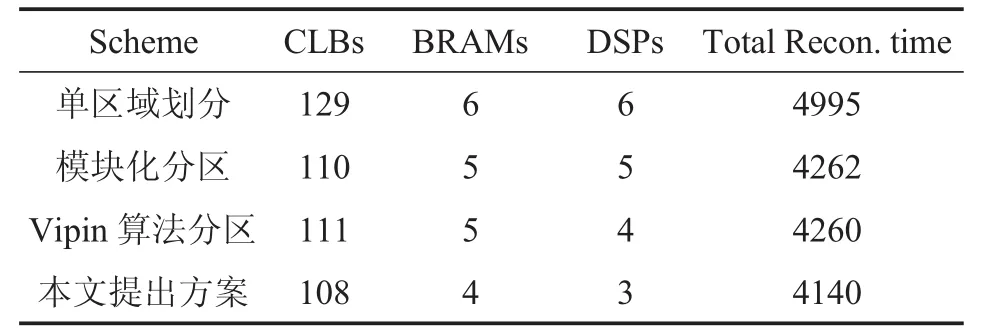
表3 4种配置模式4种RMs的用例总配置时间
同理,可以计算出所有用例的总配置时间。图11为4种方案总重配置时间的比较结果,纵坐标为总配置时间,横坐标为配置模式数量,图 11(a)、(b)、(c)、(d)分别为 RMs数量为 6、5、4、3种的情况。从图 11可以看出,单区域划分方案的时间最长,因为每次重配置需要整个RRs重构。本文提出的方案所用时间最小,小于Vipin方案,因为将同一配置中一些非连续RM模式合并在一个RR的最优化解决方案可以节省总重构区域,从而减少了重配置时间。当每个配置模式中的RM数量减少时,两种分区算法的时间是相近的。因为这种情况下,非连续的RM模式合并不会导致RR区域的面积显著减小。所以与常用方案相比,本文提出方案的总配置时间减小了30%到40%。本文提出方案与Vipin方案相比,应用越复杂总时间减少越多,6种配置模式时减少10%左右。
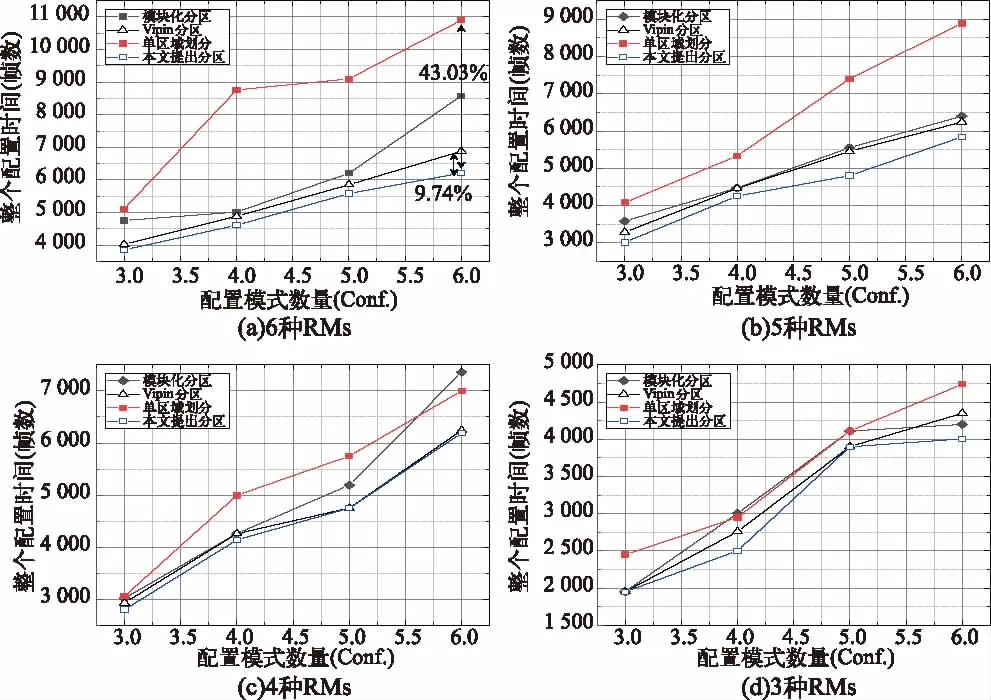
图11 4种DPR设计方案总配置时间测试结果对比
根据每种方案的分区情况,统计出每个区域包含的 CLBs、DSP、Block RAM s单元(Tiles)的数量,由公式(5)可以计算得到可重构区域面积。图12为4种设计方案的整个可重构区域面积测试结果的比较,纵坐标为总区域面积,横坐标为配置模式数量,从图中可以看出,单分区方案的RRs区域面积最小,Vipin方案在所有DPR设计方案中面积较大。本文提出的方案通过允许相同配置模式中一些非连续RM模式合并到相同的RR中,从而减少了总的RRs面积。此外,从图12(c)、(d)中可以看出,当配置模式较少时,本文提出的方案基本可以达到最小分区面积,与Vipin方案相比最多降低18.5%。
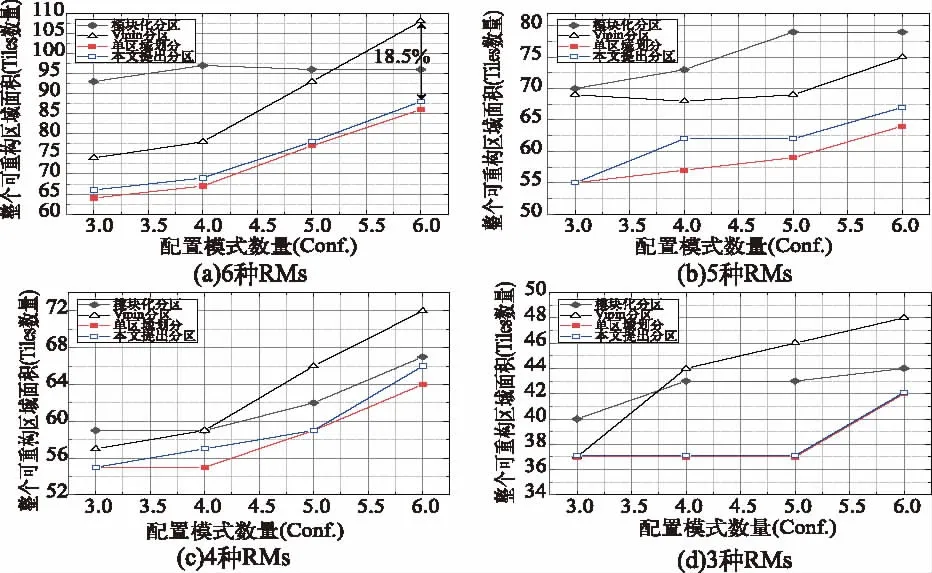
图12 4种DPR设计方案总配置区域面积测试结果对比
5 总结与讨论
可重构区域划分技术和可重构模块资源位置分配技术对部分可重构系统的性能有直接的影响。本文提出的部分可重构设计方案从总重配置时间和总重构面积两个方面进行了改进,提出一种高效的设计方案,最后基于Xilinx 7系列FPGA在KC705平台上进行了实验,实验结果与现有的3种设计方案进行对比。与Vipin算法设计方案相比,本文提出的DPR设计方案的重配置时间减少了10%,可重构面积减少了18.5%。
