基于双目单视面迭代算法
2018-09-27李熙,徐晓
李 熙, 徐 晓
(华南理工大学 物理与光电学院,广东 广州 510640)
0 引 言
本文进行了基于双目单视面(horopter)的三维重建[1,2],即利用双目单视面的理论,扩展Vieth-Muller圆到三维空间,得到horopter面[3,4],利用horopter面上的角度约束以及灰度相关性进行匹配。同时将结构光和双目单视面相结合,可达到提高复原精度的目的。但由于相机在拍照时因遮挡、光线、噪声等影响得到的两幅图像存在相似差异性,对应匹配点灰度也存在差异,增大匹配拟合误差。因此,本文利用迭代算法[5~8],多次匹配,以期得到更好的结果。
在医学CT领域,为了获得断层图像数据,学者们提出了众多图像重建的迭代算法,包括利用投影线存在的几何对称结构,引入图像重建的对称块迭代算法[9],迭代重建再投影的外插算法[10],代数迭代重建算法(ART)[11],从积分方程角度提出的图像重建迭代算法[6],利用FBPR算法将反投影算法和Richardson算法结合,通过卷积和迭代方法达到图像重建的目的[12]。通过参考以上图像重建的迭代思想,解决由于相机视野、遮挡等因素带来的两幅图像相似差异所造成的匹配粗糙的问题,本文提出了一种基于双目单视面迭代算法,即经初匹配得到的三维复原物体,投影到左右相机得到的投影图像与原始图像进行校正,校正后的图像作为三维重建的原始图,依次迭代。实验结果表明该算法可以有效改善三维复原结果。
1 双目三维重建系统
采用交叉放置的等效左相机L和右相机R[13]。根据双目单视面的原理,将图像坐标转换为角度坐标。如图1。具体的角度定义、角度坐标转换、特征匹配及三维复原的运算,参照文献[1,2,14]。
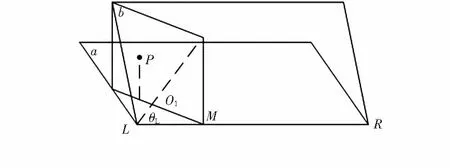
图1 坐标转换示意
2 迭代方法
2.1 三维物体投影到相机
原始左右图像经坐标转换以后,通过α,β将其网格化,即像素角度坐标都是等间隔;如图2(a)所示,系统采用角度坐标αL,αR,β将三维空间分割成P,Q,M,N等各个小的方块区域[13]。每个小的方块区域投影到相机对应的一个像素点,即坐落在每个小的方块区域的所有三维物体的点投影到相机对应的角度坐标是一致的。以P区域为例,如图2(b)所示,区域内所有点用P来表示,P、左相机L、右相机R在三维空间形成一个horopter,P对于左相机L的投影可以用αLP,β表示,对于右相机R的投影可以用αRP,β表示。如图2(d),P点在右相机R上的投影角度坐标对应的原始右图像灰度记为GRO,P点在左相机L对应投影角度坐标的像素灰度记为GL,令GL=GRO,即右图像的左投影。则点P在左图像的一个投影像素点就可以通过对应的角度坐标和灰度来表示。同理,左图像的右投影,可得到点P在右图像的对应角度坐标与灰度。
如图2(c),已知点P(xW,yW,zW)的空间三维坐标,则可以求得点P在左右图的投影角度坐标。几何换算可得
(1)
(2)
(3)
(4)
式中LR为基线长度,OW为基线中点。
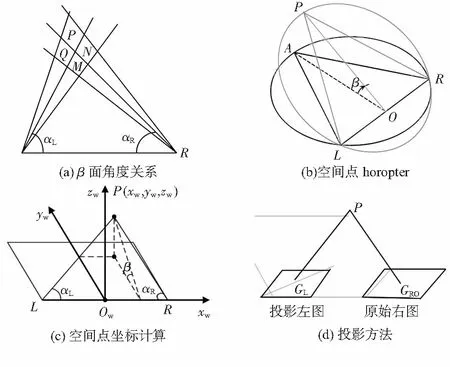
图2 三维物体投影到相机过程
2.2 迭代过程
如图3所示,迭代顺序按照三维复原—左投影校正—三维复原—右投影校正的过程依次迭代,保留最初原始左右图像数据,第一次三维重建用原始左右图像数据,复原、拟合后先投影到左相机L,与原始左图像校正以后,生成校正后左图,再与原始右图作为三维重建的输入左右图像,得到第二次的三维复原结果经拟合投影到右相机。得到的右图像投影与原始右图像校正,得到新的右图,与原始左图作为三维复原的输入左右图像,依次迭代。达到预定的迭代停止条件,停止迭代,将最终三维复原结果作为本文结果。
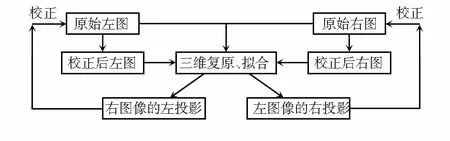
图3 迭代流程
2.3 图像校正以及迭代停止条件
图4为图像同一行的部分灰度值,通过投影图像校正原始图,原始图像ab段与投影图cd段间隔,则通过合理的平移使ab段与cd段重合,达到校正原始图部分像素点位置的目的。由于匹配算法通过提取峰值及峰值左右侧的各两个像素点作为待匹配点,且投影图像的波峰的位置与原始图像对应波峰位置基本最靠近。通过以下算法校正原始图像:
1)提取原始图像j行波峰位置U={m1,m2,…,mk}j波峰灰度Go={go1,go2,…,gok}j;
2)提取投影图像j行波峰位置V={n1,n2,…,nk};波峰灰度G={g1,g2,…,gk}j;
3)遍历j行投影图波峰位置,使每一个ni总能在U中找到最近的mu,若|ni-mu|≤σ(给定阈值)且|gi-gou|≤ω(给定阈值)则将投影图像峰值及左右两点对应的α角度坐标赋给原始图对应峰值区域,达到校正原始图像的目的。不在给定阈值条件内,不校正。
4)校正后再匹配得到的新的三维复原点云,对点云进行拟合,间接地修正了原始图像不在峰值区域的像素点。
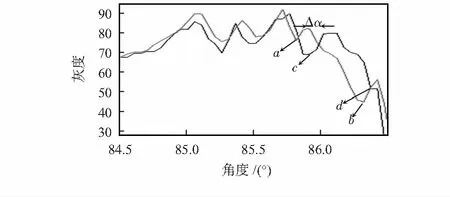
图4 校正过程
为了方便判断迭代过程,定义图像相似差异度为
(5)
式中G(i,j)为投影图像灰度,Go(i,j)为原始图像灰度。每迭代一次,计算一次η,保持不变时达到停止条件。
2.4 遮挡处理
在投影过程中会遇到遮挡问题,如图5所示,空间点A,B,C在左相机上具有相同的αL,β,而对于右相机的投影具有不同的αR,把距离L最近的点A作为投影点,剔除掉B,C被遮挡的点。
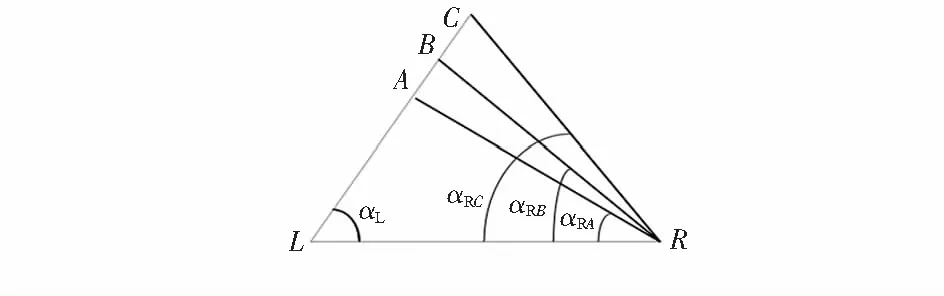
图5 遮挡区域
3 结果与讨论
采用3D绘图软件Cinema 4D模拟左右相机拍摄约翰·沃尔夫冈·冯歌德头像雕塑,得到两幅理想的1 600×1 200原始左右图像,如图6所示。其中,基线长度LR=24 cm,左右相机光轴与基线的夹角αL=αR=83°,目标物体离基线距离100 cm,理想相机的焦距为16 mm。为了实现投影迭代,在图像坐标转换成角度坐标后α,β要网格化。β取值范围[0°,11°],间隔0.03°步长,根据转换后的图像α坐标,α取值范围[99.80°,66.60°],间隔0.020 76°,使其与图像宽度1 600相等。图6(c)、图6(d)为坐标转换,α,β网格化后的图像。

图6 原始图像与坐标转换后图像
3.1 三维复原投影
利用灰度值、灰度值的一、二阶导数以及灰度相关性进行特征匹配,得到最初三维复原以及拟合后的结果如图7所示。采用MATLAB工具箱fspecial函数生成6×6窗口 高斯滤波器对其平滑处理,得到三维复原结果如图7(d)。
经过拟合得到稠密三维复原的头像经过第一次左投影,得到的投影图像如图8(a)所示。取原始左图和投影左图第200行灰度分析,如图8(b)所示。通过投影图像不断修正原始图角度,得到新的左图与原始右图继续三维重建,继续投影到右图,如图8(b)所示。
3.2 迭代停止分析即最终三维复原结果
每迭代1次计算对应的灰度相似差异度η,迭代到第3次时η基本保持在|Δη|=0.02 %范围内收敛,经4次迭代最终三维复原结果如图9(a),经高斯平滑后如图9(b)。
为了更好地展现迭代方法的效果,从不同角度比较迭代前后三维复原结果。如图10所示。
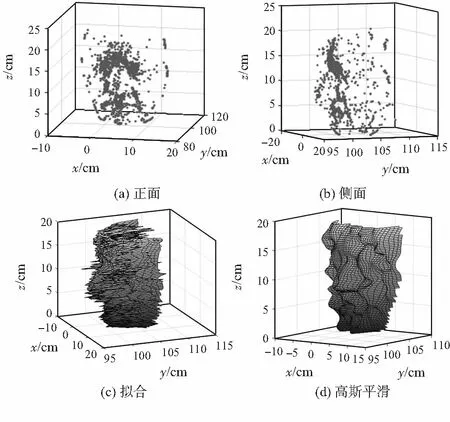
图7 初始三维复原结果

图8 投影结果
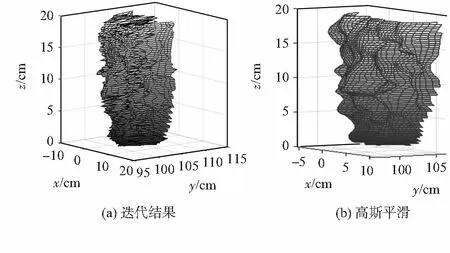
图9 最终三维复原
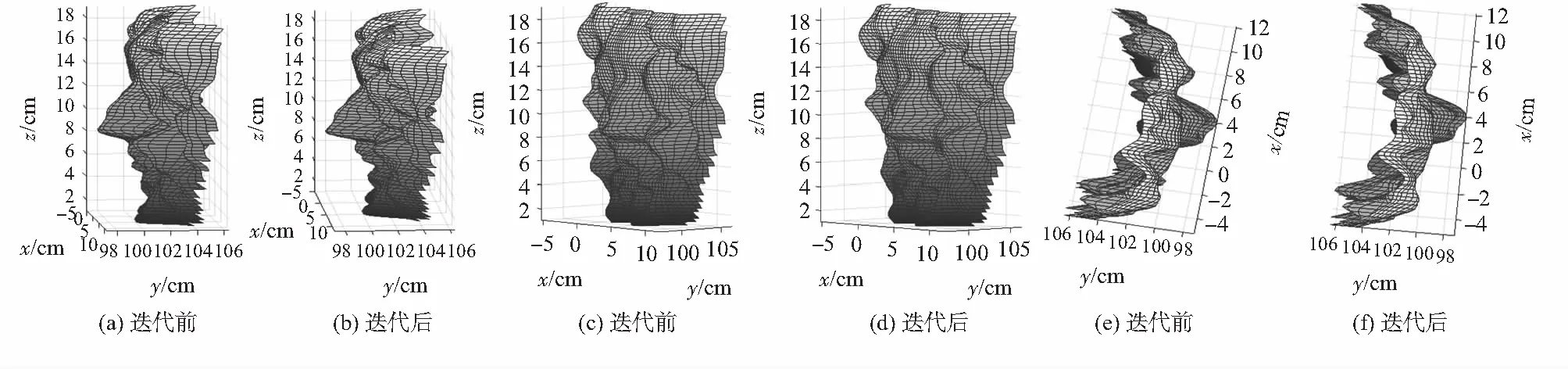
图10 迭代前后三维复原结果比较
4 结 论
本文针对已有基于双目单视面三维复原存在未充分利用数据,导致匹配粗糙的问题,提出了基于双目单视面迭代算法,通过后验证方式来校正原始图像的相似差异性,提高匹配精度。实验结果表明:迭代到第三次的时候,图像灰度相似差异度 基本保持在 内收敛,三维复原结果达到改善。
