基于六轴传感器的无线动作识别系统设计*

曾亿山, 刘 睿

(合肥工业大学 机械工程学院,安徽 合肥 230009)

0 引 言

专利《一种婴儿爬行训练机及其控制系统和控制方法》[1]设计初衷是辅助初生婴儿爬行训练。原型设备利用摄像头采集婴儿的动作并结合安置在垫子上的压力传感器数据判断的爬行意图和方向。这种识别方式受环境光线和传感器精度的制约,工作环境存在局限,本文对设备适应性差等缺点提出改进。加速度传感器和陀螺仪具有不受环境影响、可获取空间动作信息等特点，非常适合作为肢体动作识别的工具。无线传感器网络具有高效率、低成本、部署灵活等特点[2，3]。Mantyjarvi J等人将2个含有三轴加速度传感器的盒子放在测试者左右两侧腰上,识别佩戴者的不同动作[4]；Costante G等人通过智能手表内置的加速度传感器采集手臂手势作为输入方式实现手机的免提交互[5]。

本文设计基于六轴传感器的无线动作识别系统,用于识别婴儿的动作。婴儿动作不具有规律性,用单个传感器无法完成要求,需要在婴儿脊背(传感器0)、手腕(传感器1，2)、脚踝(传感器3，4)共5处佩戴传感器终端采集佩戴部位的动作信号。终端通过WiFi将数据发往服务器,根据实时动作判断爬行的意图和爬行方向。

1 系统硬件设计

硬件分为可穿戴终端和服务器。终端采用Espressif ESP8266无线模块作为控制器。惯性测量单元(inertial measurement unit,IMU)选用InvenSense MPU—6050六轴传感器,通过I2C总线与无线模块通信。终端可以实现数据的采集、预处理和传输。终端工作电压为3.3 V,锂电池经TPS63020线性稳压器降压后供电。

服务器采用MediaTek MT7621A无线开发板,其集成32 bit双核微处理器,32 MB FLASH和512 MB RAM,支持2.4,5 GHz双频段WiFi。服务器根据每个终端不同的MAC地址区分佩戴位置。

2 识别算法实现

2.1 手势定义

该系统关键是通过婴儿四肢的动作判断爬行意图。匍匐爬行的过程可分解为手臂向前伸出、膝盖弯曲腿部向躯干靠近、保持手脚位置不变、手足用力拉动身体前进等一系列动作组成。观察发现整个爬行过程,手脚移动的轨迹可以简化为水平面上的“↑”、“↗”和“↖” 3种模型,并且包含在z轴上的升降。因此将问题简化为图1中3个手势的识别。

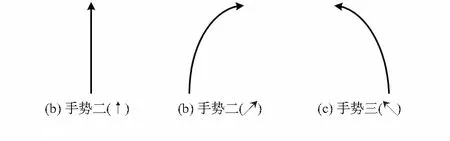
图1 3种手势的运动示意

2.2 预处理与信号提取

手势识别仅需要利用加速度信号,需要预先去除重力加速度的影响并对数据滤波。本系统对滤波要求较低,终端采集信号后经过滑动平均滤波处理后再发往服务器。

信号提取用于从连续信号中提取出仅包含动作部分的信号,如文献[6,7]的方法。本文采用加速度一阶向后差分的方法。在没有手势动作时,信号平稳；执行手势动作时,信号迅速变化。对加速度信号进行差分可反映加速度变化的剧烈程度,具体地终端获取的3种手势模版的加速度信号及其一阶向后差分信号如图2所示。

(1)

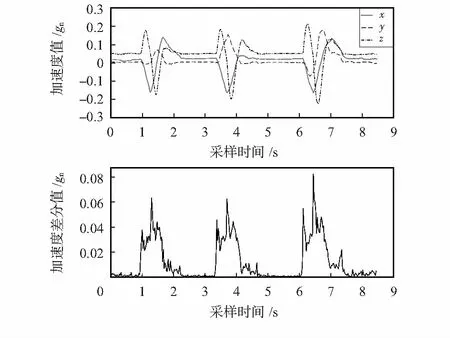
图2 加速度和加速度向后差分信号

由图可知每一个手势都对应一个加速度差分信号的主峰。手势的起点和终点通过阈值来确定,本系统采用0.02gn。差分信号阈值内数据即为有效手势信号。为避免将突发数据识别为手势,若截取起点和终点的时间小于0.15 s,则抛弃该组数据。

2.3 手势识别

现今手势识别研究中[8],考虑本系统中机能的限制,选用动态时间规整(dynamic time warping,DTW)算法较合适[9],系统的模型简单,直接利用欧氏距离计算相似度[10]。

DTW通过调整时间序列不同时间点对应元素之间的关系获得最优路径,使其能很好地度量时间序列之间的关系。假定服务器中储存的手势模板S=[s1,s2,…,sm,…,sM]和待测序列T=[t1,t2,…,tn,…，tN],其中M和N为序列中特征矢量的总帧数。m,n为矢量的时序标号。

如图3所示,在坐标系的横轴和纵轴上标出待测序列和手势模板的特征矢量,各个特征矢量之间的关系用网格表示,网格中的交叉点(n,m)表示待测序列T(n)和手势模板S(m)相交,记DTW[T(n),S(m)]为交叉点的失真。D[T,S]为待测序列与手势模板的总失真。

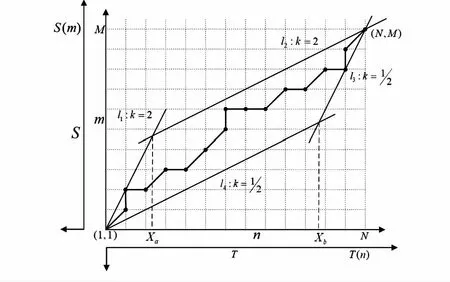
图3 DTW算法及路径限制示意

若N=M,即两个序列的长度相等有

(2)

若N≠M,定义路径代价函数d[(n,m)],其意义为从起点(1，1)出发到当前点(n,m)的累积失真,且有以下递推公式

d[(n,m)]=DTW[T(n),S(m)]+min{d[(n-1,m)],d[(n-1,m-1)],d[(n,m-1)]}

(3)

d[(1,1)]=DTW[T(1),S(1)]

(4)

式(3)表示路径中任意交叉点(n,m)前一点为(n-1,m),(n-1,m-1),(n,m-1)3个交叉点之一。根据上述公式,可从终点(N,M)反推至起点(1,1)求解最优路径,计算出长度不同的特征序列之间的最小失真度总和D[T,S]=d[(N,M)]。通过DTW算法可以使不同长度的序列相互度量。

为了避免盲目搜索,通常采用限定搜索路径中斜率的极值实现路径限制以降低算法运算量、提高速度。实际操作中虽然手势执行的速度和幅度有所不同,但各部分次序仍保持不变,因此,搜索路径必然从左下角出发,终止于右上角。通常规定以(1,1)为起点,(N,M)为终点,以经过(1,1)的直线l1,l4和经过(N,M)的直线l2,l3组成的平行四边形内进行搜索。其中l1,l3的斜率为2,l2,l4的斜率为1/2。

2.4 姿态检测

与加速度传感器不同。陀螺仪测量的是角速度,对线性机械运动敏感度较低,但其本身固有特性,工作中会产生漂移,姿态检测需要陀螺仪的测量值矫正加速度传感器测量值的错误。系统根据上一次加速度传感器测量值的估计,结合陀螺仪的测量值计算出当前时刻重力矢量的方向,再与当前时刻加速度传感器测量值加权平均,得到当前的最优估计值[11]。图4为姿态测量原理。

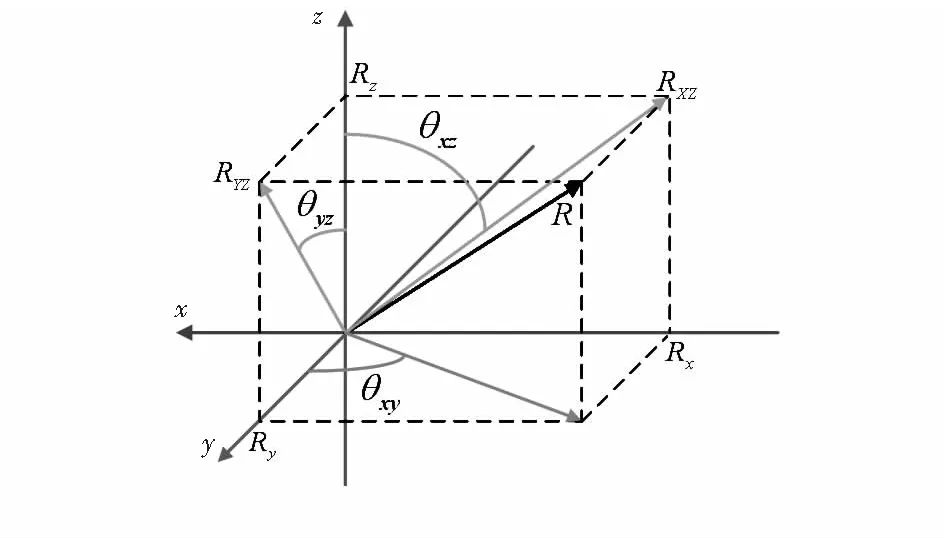
图4 姿态测量原理

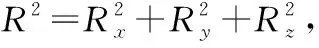
定义估计值Rest=[Rxest,Ryest,Rzest]作为算法的输出,并认为Rest(0)=Racc(0)。由图4可知tanθxz=Rx/Rz,进而求得θxz=arctan 2(Rx/Rz),利用当前加速度传感器的测量值计算陀螺仪上一时刻的角度为tan(θxz(n-1))=Rx(n-1)/Rz(n-1)。

陀螺仪的测量值为当前转动角速度ωxz,ωyz,设T为采样间隔,则得到陀螺仪在任意时刻n的角度为

(5)

引入由陀螺仪当前测量值和上一次估计值计算得到的矢量Rgvro=[Rxgvro,Rygyro,Rzgyro]。由合加速度R2可写出矢量长度,并假设长度为1 且旋转后不发生变化,有

(6)

令x=Rxgyro,y=Rygyro,z=Rzgyro,根据式(6)可得

(7)

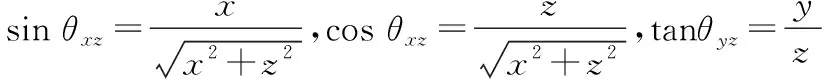
当前时刻的重力矢量估计值Rest(n)由加速度传感器当前的测量值Racc(n)和Rgyro(n)加权平均得到

(8)

式中W为陀螺仪权值,表示相对于加速度传感器,信任陀螺仪的程度,通常取5～20,本系统中取W=12。

实际工作中,只考量在与实验者身体方向相同的轴上的偏转角度,忽略其他轴上的偏转。且设定阈值为角度超过15°且持续时间超过0.75 s时系统判定为有转向意图,当角度或时间小于阈值时视为无效动作。

3 实验结果

采集手势并随机挑选3种手势各100份,其中手部和脚部分别占50份,存入服务器数据库作为模板。

结合实际情况,实验重点考察实验者开始连续执行动作到服务器给出指令所用的时间,具体某次手势的识别情况放在次要。系统工作流程如图5。

设定终端采样频率为40 Hz。传感器1～4采集加速度信号经滤波后通过WiFi传送到服务器,服务器对数据分割匹配,当超过2只传感器的手势匹配成功则直接判定为满足要求并结合脊背处传感器测出的倾斜方向输出相应指令；若只有1只传感器匹配成功,则视为无关动作；若2只传感器匹配成功,需要进一步判断是否同时为手部、脚部传感器,若是,则视为无关动作；若不是,则结合传感器0测出的倾斜方向并输出指令。

相应选取8名实验者穿戴传感器终端,距离服务器1 m处完成爬行动作15次,观察记录从实验者连续执行动作到服务器给出正确反应所用的时间,实验结果记录如表1。

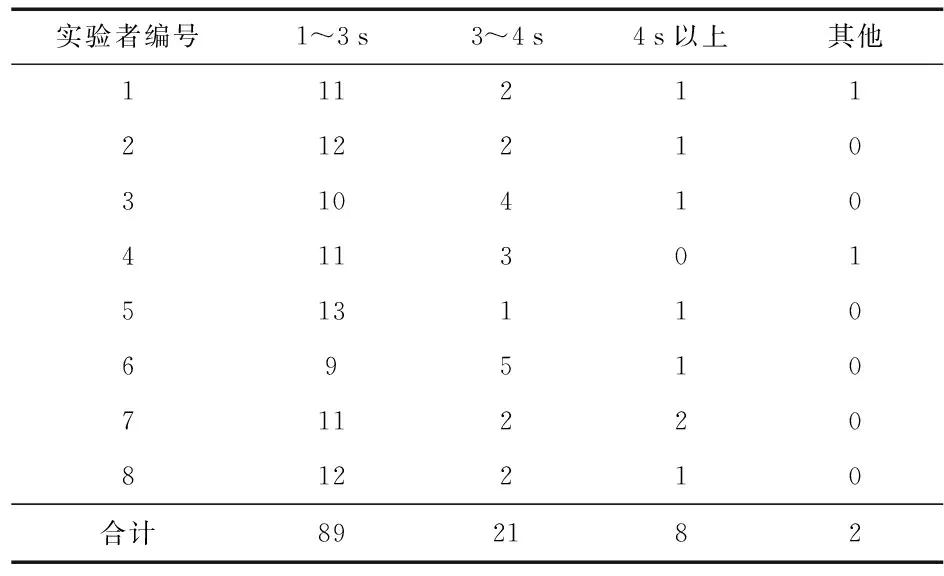
表1 系统识别时间

因为同时处理多只传感器的数据,服务器负载较大且设定了时间阈值,实验表明在动作执行1 s后服务器才能完成动作识别发出指令。其他情况是由于终端设计简单,存在供电不足等原因导致个别终端无法将数据发往服务器。

实验表明,该系统能在3 s内正确给出指令的概率为74.2 %,3～4 s内给出正确指令的概率为17.5 %,4 s以后完成识别的概率仅为6.67 %。

4 结 论

本文针对实际需要设计基于六轴传感器的无线动作识别系统,实验证明该系统可以满足实际需要。因为硬件设计简单,工作稳定性尚有不足。且基于模板匹配的手势识别有多种因素会影响识别的正确率,如手势模板的数量、执行手势的稳定性等。事实上,手势识别的应用是在线计算的过程,而文中的结论均为离线计算得到。因此,还需要对硬件和算法进一步改进,提高识别的速度和系统稳定性,以适应更加复杂的情况。