基于Duncan-Chang模型的高层建筑物分层总和法沉降计算与场地变形分析
2018-09-27江勇顺李天斌
江勇顺,唐 浩,李天斌
(1.地质灾害防治与地质坏境保护国家重点实验室(成都理工大学),成都 610059;2.四川省交通投资集团有限责任公司,成都 610041)
涉及地下空间利用的大型工程活动,由于持续性扰动,将普遍引发沉降效应[1-3]。不均匀沉降或沉降过大,都将对建筑物施工及使用产生重大影响,因而工程建设所产生的沉降问题正逐步得到重视[4-5]。引发高层建筑沉降的因素往往较为复杂,包括勘察不足或设计失误、地基土的成分差异、不良地基处理不当、建筑设计缺陷及临时堆载过大等问题[6]。目前,沉降分析的预测方法主要包括理论计算和沉降观测[7]。理论方法主要是基于本构理论通过力学分析进行沉降计算,但由于本构理论仍存在争议及缺陷,因此半经验半理论推导是目前研究的主要方式。
众所周知,地基土是一种具有复杂非线性特征的多孔材料,由于组成多样化、沉积及受外界干扰等因素共同造成了土体的各向异性。鉴于土体自身具有的复杂特性,建立一种应力-应变关系式来反映土体在各种条件下的真实情况变得十分重要,因而各种本构模型成为了研究的重点。在剑桥模型被K.H.Roscoe等[8]首先提出之后,诸如线弹性模型、弹塑性模型、流变模型等相继面世,推动了本构模型理论的进步。经过对大量本构模型的研究及相关工程实践的对比,发现Duncan-Chang模型是一种尤其适用于软土变形过程模拟的本构模型[9]。何春保等[10]通过在弹性半空间布辛奈斯克理论解的基础上推导出地基应力解,并用解析方法对Duncan-Chang模型参数进行了反演分析,反演参数较好地反映了现场沉降试验结果;何思明等[11]基于Duncan-Chang的土本构模型提出了分析地基沉降的新方法,进一步确认了土的非线性特性对单桩沉降计算具有重要影响,研究均取得了良好效果。鉴于此,本文将利用Duncan-Chang模型开展分层总和法沉降计算,并与经典沉降计算结果予以对比。
另一方面,传统的沉降监测作为辅助手段,在发现沉降变形并及时反馈,以及建立预警机制方面必不可少。当前,建筑物的变形监控及趋势预测方法较多,包括建立多元回归模型、灰色模型等理论推导方法,以及利用相关软件进行二次开发[12-14]。通过传统的沉降监测、水平位移监测和倾斜变形监测等进行离散点的位移分析是采集数据及其后续分析的基本手段[15]。由于实际建筑物的变形多为整体变形,且受到多种复杂因素影响[16],基于理论计算和实际监测结果的技术分析是掌握工程动向、判定工程质量的最有效手段,也是进行信息化施工的关键技术。高层建筑施工及工后的沉降观测,对于有效分析沉降规律,以及分析施工和工后沉降对建筑物的结构破坏、功能使用等具有不可缺少的重要意义。
本文基于一幢18层楼的高层建筑的结构特点,从观测点周围环境、观测时机和监测结果分析等方面阐述对该建筑物在施工及工后一段时期的沉降观测情况。同时,利用Duncan-Chang模型开展沉降变形计算,将计算结果与经典单向压缩分层总和法规范修正公式理论计算结果进行对比,并结合沉降监测结果综合研究在建高层建筑物的场地变形情况和时空规律特征,为今后研究类似案例提供借鉴。
1 Duncan-Chang本构模型及应用
1.1 本构模型与地基沉降
Duncan-Chang模型[17]是一种基于Kondner三轴应力-应变关系曲线建立的本构模型
σ1-σ3=ε1/(m+nε1)
(1)
其中:σ1和ε1分别为轴向应力和应变;σ3为土体围压;m、n是σ1-σ3与ε1关系曲线的拟合参数。
m=1/E0;n= 1/(σ1-σ3)μ
(2)
其中:E0为围压为σ3时土体初始变形模量。
定义Rf为土体破坏比,为破坏偏应力σ1-σ3与极限偏应力(σ1-σ3)μ之比,通常为0.75~1。可得到
(3)
其中:c为土体黏聚力;φ为内摩擦角。
由于Duncan-Chang模型仅考虑了偏应力作用下沉降量,还应加上静水压力造成的变形,因此可定义
(4)
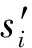

(5)
其中n为分层数。
1.2 基于Duncan-Chang模型的地基沉降分层总和法
由于不同压缩层在附加应力作用下会产生不同变形量,因此需要确定初始变形模量。在自重应力作用下,可得到铅直方向上最大主应力σ1,水平方向上最小主应力σ2=σ3,则第i压缩分层初始地应力可表示为[18]
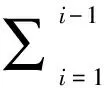
(6)
σ3ai=k0σ1ai
(7)
其中:γk和dk分别代表第k层土体的重度和厚度;σ1ai为竖直平均自重应力;σ3ai为水平平均侧压力;k0为静止土压力系数
k0=μ/(1-μ)
(8)
其中:μ为土体的泊松比。
将土体单元所受初始地应力分为自重体积应力σ3cvi和自重偏应力σ(1-3)cpi,则
σ3cvi=σ3ai;σ(1-3)cpi=σ1ai-σ3ai
(9)
由文献[18]可知,初始变形模量Eij为
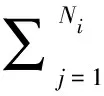
(10)
其中:m和n可由式(2)和式(3)求得。
为解决由于土的非线性特性导致力学参数变化的问题,引入分级加载思想进行沉降分析。过程如下:先将第i层土附加应力分做Mi级加载,设第i层土中第j级附加体积应力增量和附加偏应力增量分别为Δσzvij和Δσ(1-3)zpij,故

(11)

(12)
设Δε3zvij为第i层土在第j级附加体积应力增量σ3zvij作用下产生的竖向变形,采用增量胡克定律得到
(13)
其中Ezij为附加变形模量。由文献[19]可知
Ezij=Ezi(j-1)/(1-3Δε3zvij)
(14)
(15)
由此,可得
(16)
因此,采用迭代方法可得第i层土在附加体积应力和附加偏应力作用下的竖向应变之和
(17)
代入式(4)可得
(18)
代入式(5)即可得地基总沉降量。
1.3 地基沉降计算结果
根据本文研究对象的建筑特点并结合经验可知,本项目由18层地上建筑与1层地下车库组成,采用筏板基础,该基础主要发生整体沉降及部分挠曲变形,其中间位置的沉降量往往大于边缘部分3~4倍。根据保守原则,首先计算其中心位置的基础最终沉降量。
以1号楼为例,其基础宽度(b)为25 m,长度(l)为28 m。分成4个均等矩形后,宽度b/2为12.5 m,长度l/2为14 m。基础埋置深度(z)为6.06 m,地下水枯水期埋深约2 m。采用Duncan-Chang模型对该建筑物沉降分析进行计算。基于安全考量,取Rf=1.0。根据建筑地基基础设计规范(GB50007-2011),当基础宽度在30 m以内时,地基的变形深度按简化公式计算,得到zn=18.6 m;结合场地的地层岩性特点,拟定计算深度为22.0 m,即达中粗砂地层。分层厚度根据规范(b>8 m取1 m)均取1 m,因此N=22。利用布辛奈斯克解计算,首先得到基底位置的自重应力为76.15 kPa,由土压力观测得知基底平均压力p=166.2 kPa,因此可得到基底平均附加压力p0=90.05 kPa。相应地,在求得基底附加压力后得到各土层附加应力σ1zi和σ3zi,并进行5级加载(即Mi=5)。由此计算得到各压缩层的沉降si,累加得到地基土最终沉降量为58.34 mm。
2 经典分层总和法计算基础最终沉降
经典沉降计算方式包括单向压缩沉降计算法、三向变形计算法、剑桥模型法和其他方法。其中,单向压缩沉降计算法主要包括分层总和法单向压缩基本公式、规范修正公式法和考虑三向变形效应的单向压缩法。众所周知,分层总和法规范修正公式法是应用较多的方法之一。有研究表明,单向压缩沉降计算在基础面积远大于压缩土层厚度时计算结果更为精确[20]。因此,结合拟建建筑物采用具有较大面积的筏板基础这一客观因素,本文将采用规范修正公式法计算建筑荷载下中心点的最终沉降量。有关规范修正公式法计算基础最终沉降量的具体方法参见文献[21],本文不再赘述。
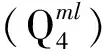
将基础等分成以中心点为形心的4个部分,通过角点法计算中心点以下由该基础荷载引起的地基竖向附加应力;利用公式
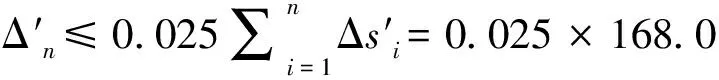
=0.63×168=105.84 mm。
3 场地监测及关键点计算
通过在建筑物主体及邻近建筑物上布置监测点,定期监测和分析建筑物在各施工阶段的沉降量和分布规律,由此总结建筑物在施工阶段的沉降响应特征及规律。
本次监测共设置沉降观测点19个,根据建筑物的结构特点及邻近建筑物位置均匀布设在外围主体结构上(相邻两点距离15~25 m)。建筑物沉降观测应在建筑物主体结构施工时每3层观测1次,竣工后观测2次,共计8次。现场监测点位布置及重点监控点位如图1,其中BM7、BM13为本次分析的重要点位,分布于场地的西北角和东南角。
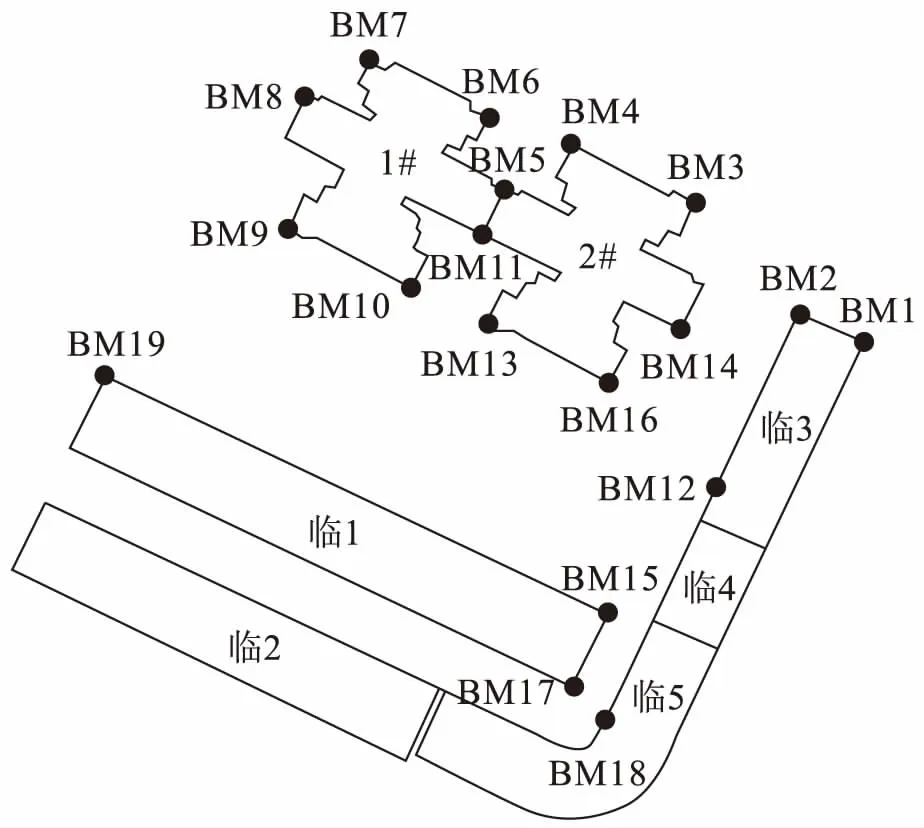
图1 19个沉降观测点位Fig.1 Diagram showing positions of 19 settlement observation points
根据现场勘查,建设区内1号和2号楼周边区域情况差异显著。其中,2号楼场地边缘距离南侧邻近既有建筑物“临1”约4.0 m,为老式多层居民楼,高7层;距离东侧邻近建筑物“临3”“临4”和“临5”约为2.0 m,也是多层建筑。1号楼与2号楼环境差异较大,其场地北面及西面5 m范围内没有建筑物,属于空旷区域。这种场地周边建筑环境不同的特点必然对场地内建筑物在施工期及工后一定时期内的沉降变化产生一定影响,为产生沉降的时空差异化提供了条件。
如图1所示,BM13监测点属于2号楼,位于整个拟建场地的南面,其东、南两个方向均受邻近建筑物影响。与其相反,BM7监测点属于1号楼,位于整个场地的西北角,其西北两面均为空旷区域,显然侧限较少。由于两个点位空间位置不同、周围环境不同,因此有必要对BM7与BM13的地基变形计算结果进行对比。
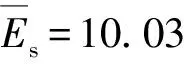
=37.3 mm。

4 结果分析
4.1 不同点位沉降差异
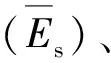
由此可见,2个点位所在区域不同,受到的环境制约具有差异,因而基地平均附加压力p0因基底所在深度范围内的地层岩性不同而有所不同,BM7为90.05 kPa,BM13为96.61 kPa;沉降变形计算深度zn根据规范标准,并经过单层压缩量与分层总和法累计沉降量代入公式验算,符合规范要求;压缩模量当量值根据附加应力系数沿土层厚度的积分值与各层土的压缩模量综合求得,BM7为9.49 MPa,BM13为10.03 MPa。受以上因素综合影响,两个点位的最终沉降量不同,显然,BM13点受到了邻近建筑物的影响,沉降量小于BM7。

表1 BM7和BM13计算结果对比Table 1 Correlation of calculation results for BM7 and BM13
中心点位和建筑物边部的沉降计算结果对比如表2。
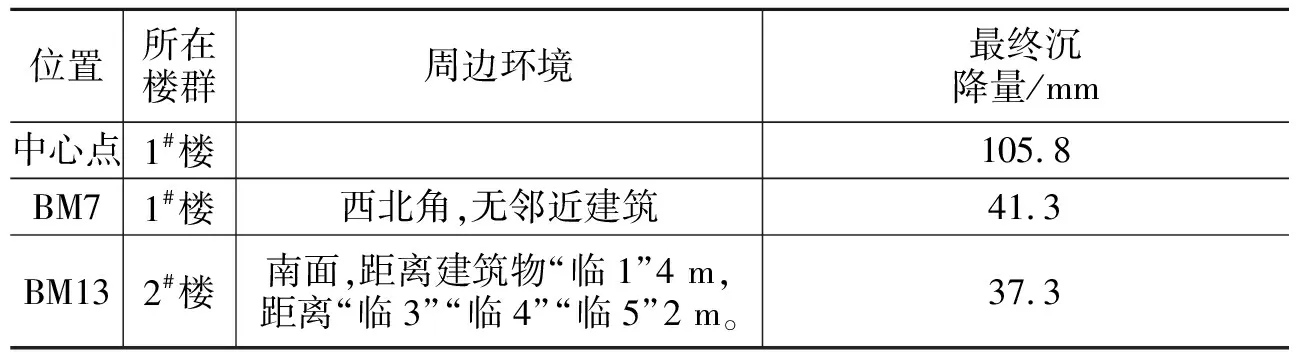
表2 多点位沉降量对比Table 2 Comparison of settlement at different points
从基础最终沉降量来看,显然BM7与BM13处于同一数量级,明显小于中心位置,印证了采用筏板基础的建筑物沉降量具有“中心较大、四周较小”的挠曲变形特点。
4.2 计算结果对比及变形趋势分析
本文分别利用Duncan-Chang模型和规范公式法经典理论对中心点基础最终沉降量进行了计算,将计算与分析结果进行对比分析(表3)。
由此可以看出,Duncan-Chang模型计算结果更为接近工程实际。与经典沉降理论相比,Duncan-Chang模型避免了选取经验系数来修正沉降量的人为误差,同时也避免了在压缩曲线(e-p曲线)上确定受压前后孔隙比时可能存在的错误,因而具有一定优越性。不过,从表3可以看出,基础的沉降不仅局限于施工过程,在工后由于土体的继续固结、人为堆载和风荷载等多种因素,仍然会产生一定的沉降变形,在今后预测沉降趋势判断时应引起足够重视,并需要开展长期监测。为此,本文选取了某一施工阶段及主体完成后的工后监测结果来分析各点位的沉降趋势(图2)。
需要说明的是,BM1、BM2、BM15~BM19为邻近建筑物上的监测点,本文只观测了其在建设期间的沉降情况(图2),由于工后其沉降极其微小,因而没有继续观测。由图2可见,不同监测点在监测周期内具有明显的时空规律,即沉降绝对值随着土体不断固结而逐渐减小,且建设期间的相对沉降量均大于工后沉降,可以认为到某一时点建筑物的沉降已可忽略不计,处于安全状态。在不同阶段,沉降较大的点位均集中在西北方,特别是BM5~BM8监测点。有关规律在全寿命周期内均有所体现,也再次证明了修建的建筑物不同程度地受到了相邻建筑物的影响。

表3 沉降计算结果对比分析Table 3 Comparative analysis of settlement calculation results
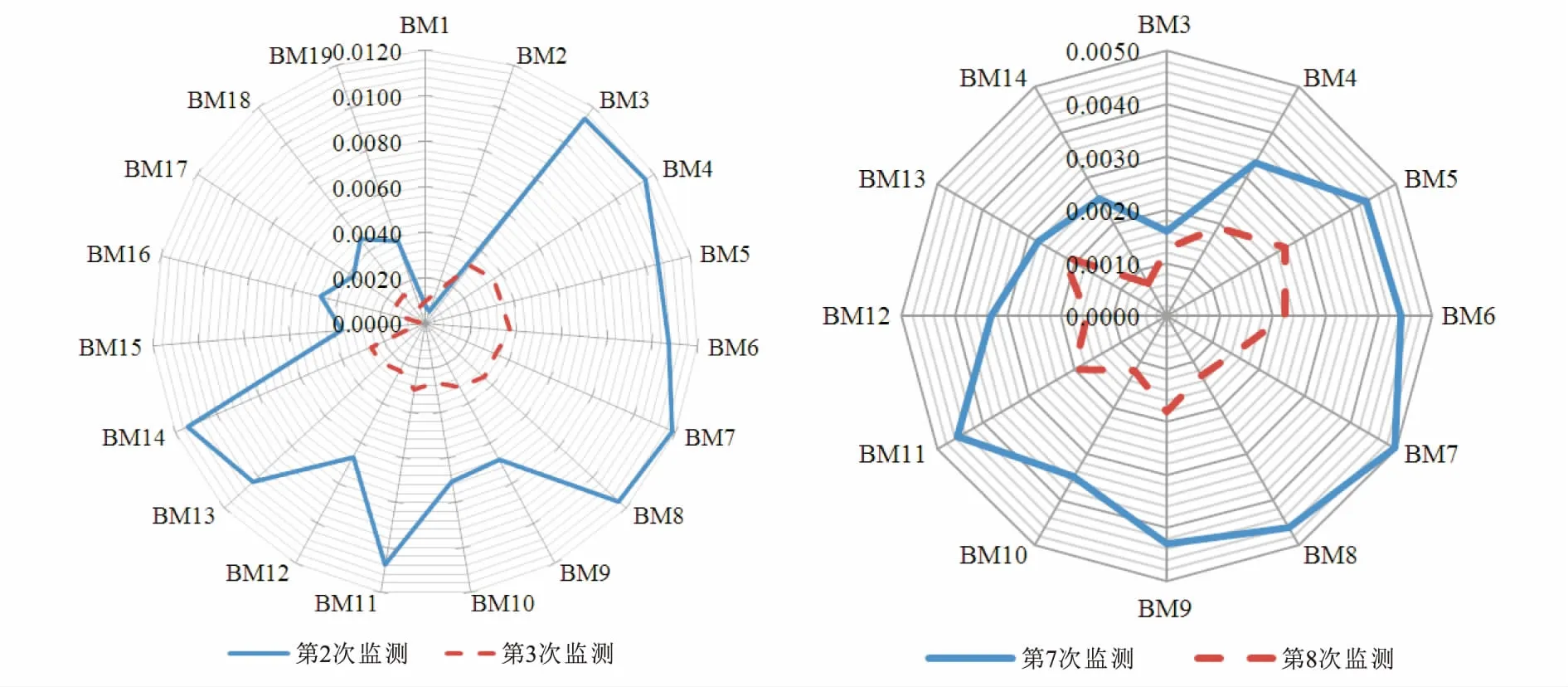
图2 相邻2次监测沉降量Fig.2 Monitored settlement in two adjacent cases(A)建设期监测数据样本; (B)工后沉降监测数据样本
5 结论及建议
通过对建筑场地内典型位置在特定时期荷重条件下采用基于Duncan-Chang 模型的分层总和法和传统的单向压缩分层总和法规范修正公式进行地基沉降变形计算,并结合多组点位沉降量持续监测结果,可以得到以下结论:
a.基于Duncan-Chang模型的沉降变形计算方法在理论上规避了分层总和法规范修正公式计算中选取修正系数时的系统误差,也避免了在e-p曲线上确定2个孔隙比时的偶然误差,其优越性较为显著,本案例中计算结果也更加接近于实测值。
b.经计算得到的1号楼基础中心位置沉降量远大于以BM7、BM13为代表的建筑边缘位置,证明了筏板基础的建筑物沉降具有差异性,即存在“中间下凹、四周上翘”的挠曲变形特点。
c.以BM13为代表的监测点由于受到周边既有建筑物限制,在施工和工后阶段沉降量受到影响,最终沉降量小于周边空旷的BM7点位,说明沉降量与周边相邻建筑物有关。
d.对比计算和监测结果可知,监测数据可以真实反映实际沉降情况;而计算结果往往存在偏差,但可作为预测沉降变形趋势的有效方式。
e.对于高层建筑集群或线性工程来说,由于布置监测点位的数量有限,导致监测盲区较多。因此,通过修正理论计算和实时反馈监测手段相结合,能够较好地达到信息化施工的目的。
需要指出的是,基于Duncan-Chang非线性本构模型的地基沉降分层总和法虽然适用于软土变形,但仍不能准确反映相关塑性变形情况,下一步将基于整个变形过程来改进和完善相关本构模型。同时,鉴于篇幅所限,本文未进行多案例、全区域沉降计算,选取的计算及监测点位不够充分,今后还将适当研究。
