基于融合概率盒的指标灵敏度分析方法

任东磊 王清心 丁家满

摘要：传统灵敏度分析方法大多忽略了指标不确定性问题，难以反映指标不确定性对评估结果的影响程度，导致关键指标辨识困难。为此，在不精确概率的数学性质基础上，提出基于融合概率盒的不确定性指标灵敏度分析方法。首先针对指标数据的分布特点采用不同方法建立指标概率盒模型，然后进行指标概率盒两两交叉融合运算，获得每次融合后的概率盒模型，最后通过计算融合后概率盒模型积分面积变化分析指标的灵敏度。与传统方法比较，结果表明该方法不仅能有效辨识出关键指标，而且给出的灵敏度排序结果与传统方法相比具有更高的区分度。

关键词：概率盒；不确定性指标；融合；灵敏度分析

DOI：10.11907/rjdk.173051

中图分类号：TP301

文献标识码：A文章编号：1672-7800（2018）007-0070-05

Abstract：Thetraditionalsensitivityanalysismethodmostlyignoretheuncertaintyoftheindex，anditisdifficulttoreflecttheinfluenceofuncertaintyonassessmentresults.Onthebasisofthemathematicalpropertieswithimpreciseprobability，thispaperputsforwardasensitivityanalysismethodbasedonfusedprobabilitybox.Firstly，accordingtothedistributioncharacteristicsofindexdatatheprobabilityboxmodelisestablishedbycorrespondingmodelingmethods，andtheneachtwoprobabilityboxesarefused，thuswecangetfusedprobabilityboxmodel；finally，thesensitivityoftheindexisanalyzedbytheratioofareaintegralbetweenthefusedprobabilityboxes.Theanalysisresultshowsthattheproposedmethodcannotonlyhavemoreeffectiveidentificationofthekeyindicatorsthantraditionalmethods，butalsocanobtainthesensitivityresultswithhigherdifferentiation.

KeyWords：probabilitybox；uncertainindex；fusion；sensitivityanalysis

0引言

为防止规划决策过程出现偏差，决策者不仅要对关键指标进行识别，并且要在众多指标中进行筛选，过滤出对方案影响小的指标以及分析各指标影响程度。因此，研究规划方案中指标的灵敏度尤为重要[1]。

灵敏度分析[2]指在一个数学模型中根据输入变量的变化观测输出变量的变化，确定灵敏度大小的方法。在指标权重赋值、设计可靠性和方案决策中，不确定指标数据的正确表达是灵敏度分析的关键环节[3]。灵敏度分析有许多经典方法，如非参数法[4]、方差分析法[5]以及矩独立分析法[6]。其中对指标不确定性描述和表达，尤其对随机不确定性表达方面，均值、方差较为常用，相当于用不确定指标数据的一个特征值描述不确定信息。在指标确定的情况下，可采用直接求导法对灵敏度进行计算；在指标不确定且变量分布有规律的情况下，常用方差分析法等进行灵敏度分析。

事实上许多不确定变量没有准确的规律可循，即便大体符合某种分布也存在漂移现象，比如某个指标基本符合正态分布，但其均值和方差不是固定值，而是区间。在决策分析中随机不确定性与认知不确定性往往同时存在。因此，如何正确表达指标数据的不确定性成为灵敏度分析的重中之重。

在证据理论基础上发展而来的概率盒理论[7]，能较好地统一表达随机不确定性和认知不确定性[8]，从其数学定义来看，概率盒用于表达不确定性变量漂移现象更为擅长，得到了广泛应用[9-10]。例如文献[11]使用概率盒解决多项式系统的可靠性问题，文献[12]将其用于处理工程分析中的不精确概率问题。本文提出基于融合概率盒的灵敏度分析方法，通过概率盒表达这些不确定指标。首先对指标进行概率盒建模，然后进行指标概率盒两两交叉融合运算，得到新的融合概率盒模型，最后根据融合概率盒两两之间的面积积分比值分析指标的灵敏度。

1概率盒及相关理论

1.1概率盒

概率盒由美国桑迪亚国家实验室（SandiaNationalLaboratory）提出，在累積概率分布函数（CumulativeProbabilityDistributionFunction，简称CDF）中引入区间类型界限，这种界限称之为“概率盒”，它既可表达随机不确定性，也可表达认知不确定性。

定义一个随机变量X属于集合（Ω，A），同样A为Ω的子集。因为累积分布函数是非递减函数，并且累积分布函数F（x）值域为R[0，1]，累积分布函数F（x）界定在（F-（x），F-（x））之间，这种表示方法称之为概率盒或概率包络（P-box）。F-（x）称为F（x）的下边界，F-（x）称为F（x）的上边界。概率盒如图1所示。

概率盒可这样理解：不管或者不必知道概率符合的分布是什么，规定一个上边界和下边界，要求累积分布处于这个范围，这个范围即称为概率盒。这种分析通过对不确定性分布函数周围进行边界划分，保证产生的界限完全处于累积分布函数之间。

1.2D-S结构体

同理，从图2可知概率盒可转化为多个D-S结构体，这个过程称之为概率盒的离散化。

2基于融合概率盒的指标灵敏度分析方法

2.1概率盒建模算法

将所知的经验信息和理论信息表现在概率盒并对概率盒建模的方法很多，专家估计法可根据已经掌握的分布或专家的经验得到某一不确定变量的概率分布，进而得到概率盒的上下界，是一种最常用的方法，也是最容易得到输入模型的方法。所以，当不确定信息足够时，该概率盒会退化为累积概率分布函数。多数情况下由于所知局限，一个分布的参数是不确定的，只能由经验估算出一个大致区间，此时可直接计算出概率盒的上下界。例如，对于一个不确定变量A服从正太分布，其均值μ∈[0，1]，方差σ∈[2，3]，就可知道概率盒的左上边界是以0为均值，2为方差的累积概率分布函数。同理，概率盒的左下边界是均值为0方差为3的累积概率分布函数，右下边界是均值为1方差为2的累积概率分布函数，右上边界是均值为1方差为3的累积概率分布函数，如图3所示。

概率盒建模方法还有参数建模、鲁棒贝叶斯、测量观测法等等。

概率盒建模算法步骤：

（1）获取指标的历史数据，采集数据特征进行不确定数据概率盒建模分类。①如果数据符合某种分布，可直接选取其密度函数或概率分布函数作为模型；②如果数据符合某种分布，但其分布参数在某个区间波动，则选择参数建模法。首先将数据分为n组，根据每组的最大值、最小值以及随机不确定性的概率均值累计分布性质，分别以最大值、最小值作为积分的上下界，累积出每组的概率上界和概率下界，最后选取所有组中概率下界最小的概率作为概率盒下界，选取所有组中概率上界最大的作为概率盒上界；③如果数据不符合以上情况，可直接使用概率盒的定义建模。

（2）进行分布累积，得到概率盒上下界。

（3）根据累积分布后的函数画出概率盒示意图。

2.2概率盒融合

2.2.1交集融合

交集融合是利用最小区域作为融合结果，该区域的所有估计是一致且高度可信的。

对于任意x都有F-*（x）≤F-*（x）。使用交集对概率盒进行融合，实质就是取各概率盒的下界最大值和上界最小值。使用交集融合的条件是所有信息源必须包含真实值，但是交集融合的容错性差，一旦信息源出现奇异源将可能得到空集。

交集融合的一般步骤是：先将所有信息源构建为概率盒，然后等信度离散成相同的份数，利用上述交集公式对每一份等信度概率盒进行融合，最后累积即可得到融合结果。

2.2.2包络融合

包络融合实质就是并集融合，取概率盒的下界最小值和上界最大值，和交集融合相反。包络法适用于信息源可靠性未知的情况。

使用包络法融合概率分布、概率盒或D-S结构体得到的结果仍是概率盒，包络法是最开放的融合方法，但是其融合结果的精确度也最差，一旦奇异源出现，决策的精度就会大打折扣。

2.2.3D-S规则融合

证据理论以焦元为基本计算单位，所以必须将概率盒离散为焦元的形式。基于D-S合成规则的概率盒融合算法主要运用证据理论中的D-S合成规则计算离散后的证据结构体，最终累积后得到融合结果，利用的便是概率盒与D-S结构体之间的关系。其步骤为：先将概率盒正则离散成D-S结构体，将每一份等信度的D-S结构体运用证据合成规则进行融合，然后依据得到的结构体累积即可得到融合的概率盒。

3基于融合概率盒的指标灵敏度分析算法

概率盒的概率边界不是传统的近似值或一个估计区间，所以数据的随机不确定性和认知不确定性描述会更加完整。可以全面考虑不确定数据的性质，例如分布参数的不确定性、分布形状、间隔依赖。因此，概率盒可根据不确定数据的简单特征构建出概率界限带入相关分析中，这比传统的计算方法全面。下例简单展示了本文方法思想。

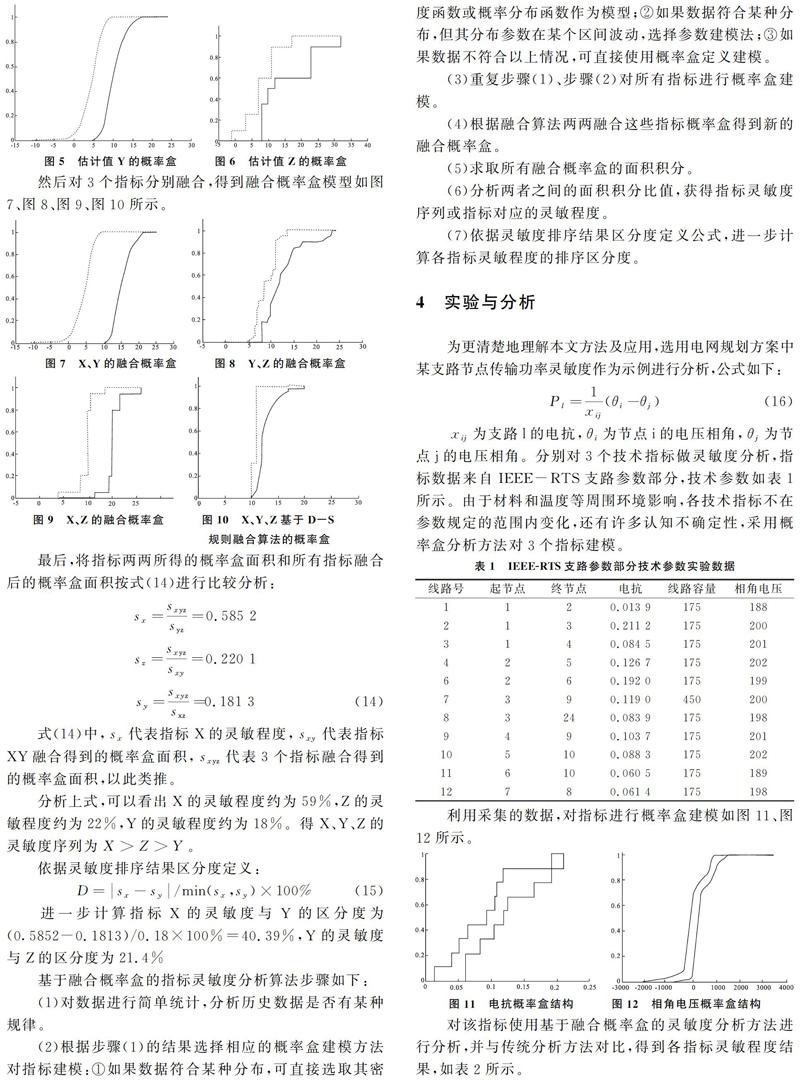
首先搜集整理历史数据，对其建模如图4、图5、图6所示。

然后对3个指标分别融合，得到融合概率盒模型如图7、图8、图9、图10所示。

最后，将指标两两所得的概率盒面积和所有指标融合后的概率盒面积按式（14）进行比较分析：

式（14）中，sx代表指标X的灵敏程度，sxy代表指标XY融合得到的概率盒面积，sxyz代表3个指标融合得到的概率盒面积，以此类推。

分析上式，可以看出X的灵敏程度约为59%，Z的灵敏程度约为22%，Y的灵敏程度约为18%。得X、Y、Z的灵敏度序列为X>Z>Y。

依据灵敏度排序结果区分度定义：

进一步计算指标X的灵敏度与Y的区分度为（0.5852-0.1813）/0.18×100%=40.39%，Y的灵敏度与Z的区分度为21.4%

基于融合概率盒的指标灵敏度分析算法步骤如下：

（1）对数据进行简单统计，分析历史数据是否有某種规律。

（2）根据步骤（1）的结果选择相应的概率盒建模方法对指标建模：①如果数据符合某种分布，可直接选取其密度函数或概率分布函数作为模型；②如果数据符合某种分布，但其分布参数在某个区间波动，选择参数建模法；③如果数据不符合以上情况，可直接使用概率盒定义建模。

（3）重复步骤（1）、步骤（2）对所有指标进行概率盒建模。

（4）根据融合算法两两融合这些指标概率盒得到新的融合概率盒。

（5）求取所有融合概率盒的面积积分。

（6）分析两者之间的面积积分比值，获得指标灵敏度序列或指标对应的灵敏程度。

（7）依据灵敏度排序结果区分度定义公式，进一步计算各指标灵敏程度的排序区分度。

4实验与分析

为更清楚地理解本文方法及应用，选用电网规划方案中某支路节点传输功率灵敏度作为示例进行分析，公式如下：

xij为支路l的电抗，θi为节点i的电压相角，θj为节点j的电压相角。分别对3个技术指标做灵敏度分析，指标数据来自IEEE-RTS支路参数部分，技术参数如表1所示。由于材料和温度等周围环境影响，各技术指标不在参数规定的范围内变化，还有许多认知不确定性，采用概率盒分析方法对3个指标建模。

利用采集的数据，对指标进行概率盒建模如图11、图12所示。

对该指标使用基于融合概率盒的灵敏度分析方法进行分析，并与传统分析方法对比，得到各指标灵敏程度结果，如表2所示。

由表2可以看出，3种方法计算出的灵敏度排序基本相同：θj>θi>xij，均辨识出指标θj最敏感，属于关键指标。

根据表2数据，求导法认为指标θi与xij一样敏感，难以区别，而方差法和本文方法可以辨识出指标θi明显比xij敏感，更为关键。其中方差法和本文方法得出θi与xij的区分度分别为45%、55.5%，θj与θi的区分度分别为40.6%、50%。在相同数据集中本文方法计算出的灵敏度排序结果区分度较高，究其原因是本文方法在对指标建模时，将所有不确定性都包含在概率盒中，在之后的每个计算步骤中，差异不断放大，最终的排序结果差异也愈发明显，区分度更高。由此可见，本文方法在采用传统评价方法难以给出灵敏度排序的情况下更具实用性。

5结语

利用概率盒描述不确定指标数据，充分描述了不确定数据的性质，通过对不确定指标数据进行概率盒建模，以及基于融合概率盒的分析方法进行灵敏度分析，可更精确地得出影响模型变化的指标，发现指标对模型的影响程度，提高了灵敏度分析精度指标，有助于决策者分析各指标的权重分布。本文方法侧重点是对不确定指标的灵敏度分析，可以应用于结构可靠性灵敏度分析，对某种结构风险进行评估，还可对指标相关性进行研究。

参考文献：

[1]陈光，林振智，周浩，等.电网规划方案决策的概率灵敏度分析[J].电力系统自动化，2013，37（9）：41-46.

[2]DANGC，IONESCUBUJORM，NAVONAIM.SensitivityandUncertaintyAnalysis，VolumeII[EB/OL].http：//www.doc88.com/p-6601231009924.html.

[3]FERSONS，TUCKERWT.Sensitivityanalysisusingprobabilitybounding[J].ReliabilityEngineering&SystemSafety;，2006，91（10-11）：1435-1442.

[4]羅毅，刘峰，刘向杰.基于主成分-遗传神经网络的短期风电功率预测[J].电力系统保护与控制，2012，40（23）：47-53.

[5]师洪涛，杨静玲，丁茂生，等.基于小波-BP神经网络的短期风电功率预测方法[J].电力系统自动化，2011，35（16）：44-48.

[6]范高峰，王伟胜，刘纯.基于人工神经网络的风电功率预测[J].中国机电工程学报，2008，28（34）：118-123.

[7]FERSONS，KREINOVICHV，GINZBURGL，etal.ConstructingprobabilityboxesandDempster-Shaferstructures[R].SAND2003-4015，Albuquerque，NM：SandiaNationalLaboratories，2003.

[8]杨旭锋.含认知不确定性参数的高效高精度可靠性分析方法研究[D].西安：西北工业大学，2016.

[9]黄心，王清心，丁家满.基于概率盒理论的电网规划方案中指标不确定性建模[J].信息与控制，2016，45（3）：272-277.

[10]TUCKERWT，FERSONS.Sensitivityinriskanalyseswithuncertainnumbers.[J].FersonSKreinovich，2006（2）：156-159.

[11]CRESPOLG，KENNYSP，GIESYDP.Reliabilityanalysisofpolynomialsystemssubjecttop-boxuncertainties[J].MechanicalSystems&SignalProcessing;，2013，37（1-2）：121-136.

[12]BEERM，FERSONS，KREINOVICHV.Impreciseprobabilitiesinengineeringanalyses[J].MechanicalSystems&SignalProcessing;，2013，37（1-2）：4-29.

（责任编辑：杜能钢）