基于分组主成分分析法的大学生综合素质测评研究

侯小洁，张俊华

（商洛学院 生物医药与食品工程学院，陕西 商洛 726000）

大学生综合素质测评是对学生在校表现和各方面素质的测定和评价，是学生全面发展的导向目标，也是对学生进行教育和管理的重要环节之一[1-2].测评结果体现学生的综合素质，可作为奖助学金评定、评优树模、确定入党积极分子以及就业推荐等工作的根本依据.目前，我国高校在对大学生综合素质测评成绩进行计算时，多采用简单加和法，即将加权平均成绩与其他指标量化值直接相加[3].这种方法指标模糊，计算方法不科学，无法真正体现学生的真实情况，导致综合素质测评失去其本身对学生的激励和指引作用.分组主成分分析法能对多维变量进行降维处理,避免了传统简单加和法中存在的指标间信息重叠，更加客观地确定各指标的权重，提高了测评结果的科学性[4].本文采用分组主成分分析法，选取了7个测评指标，从指标的相关性出发构建大学生综合素质测评模型，并将测评结果和常规算法进行了对比研究.

1 研究方法

1.1 测评指标选取

依据科学、公开、合理、全面的原则，通过咨询专家和调查研究，选取7个评价指标.

X1：身心素质指标.学生的大学体育、心理健康课、体能测试成绩的加权平均值，其中体能测试成绩按1个学分计.

X2：课程指标.除去外语、计算机、体育、心理健康、实验课外所有课程成绩的加权平均值，公式：课程指标

X3：外语指标.学生的外语成绩的加权平均值，四六级成绩换算成百分制，分别按2个、3个学分计.

X4：计算机能力指标.学生计算机课程成绩的加权平均值，计算机等级考试按2个学分计.

X5：实验技能指标.学生实验课、专业实习成绩的加权平均值.

X6：德育指标.学生参加政治学习、获得荣誉、做好事加分，违反校规校纪、不文明行为扣分总和.

X7：能力指标.学生参加各类比赛获奖、担任学生干部、发表文章、参加社会实践活动加分总和.

1.2 分组主成分分析法构建评价模型

设参与测评人数为n，每个测评对象有7个评价指标，则形成的原始数据构成一个n×7维的矩阵（Xij）n×7，其中i=1，2，…7.将原始数据进行标准化处理，求出矩阵（Zij）n×7的相关系数矩阵R、特征值λi(i=1，2，…p)和对应的特征向量 Li(i=1，2，…p)，其中R=（rij）p×p[5].按主成分法提取累计贡献率大于85%的m个主成分，将初始因子载荷矩阵采用方差最大旋转法进行旋转，得到旋转因子载荷矩阵[6].从指标的相关性出发，按照各因子中具有较大荷载的指标分为同一组的原则[7]，将P个指标分成k组.分别对各组指标进行主成分分析，由于组内各指标相关性较强，故只提取第一主成分并求出第一主成分的得分Cj(i=1，2，…k)[8].以各组的第一主成分为各组得分，旋转后各因子的方差贡献率作为权重wj=，即可建立大学生综合评价模型，（i=1，2，…7；j=1，2，…k）.

2 实例研究

本文以商洛学院食品科学与工程专业2015级68名学生为例，选取2015—2016学年的各科成绩、德育素质成绩和能力素质成绩为原始数据.

2.1 大学生综合素质测评模型的构建

参与测评人数为68，每个测评对象有7个评价指标，则形成的原始数据构成一个68×7维的矩阵.用SPSS软件将原始数据进行标准化处理，然后进行主成分分析.KMO和Bartlett检验结果显示，KMO值为0.656，大于0.6，Bartlett球度度检验的Sig值小于显著水平0.05，说明原有指标间存在相关关系，符合因子分析的条件，可以进行因子分析[9-10]，并进一步完成主成分分析.

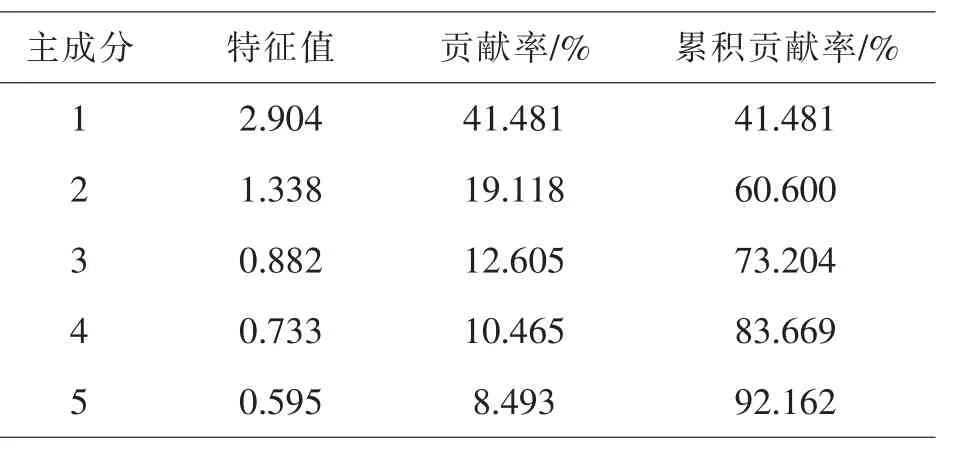
表1 各主成分的特征值和累计贡献率

表1显示前5个主成分的累积贡献率达92.162%，满足≥85%的条件，故提取前5个主成分.采用方差最大旋转法进行因子正交旋转后，得到如表2所示的旋转因子载荷矩阵.从旋转因子载荷矩阵可以看出，德育指标X6和能力指标X7在主成分1上载荷较高，故将主成分1命名为德育和能力因子；课程指标X2和实验技能X5在主成分2上载荷较高，故将主成分2命名为专业能力因子；指标 X1、X3、X4分别在主成分 3、4、5 上荷载较高，分别为身心素质因子、计算机能力因子和外语能力因子.

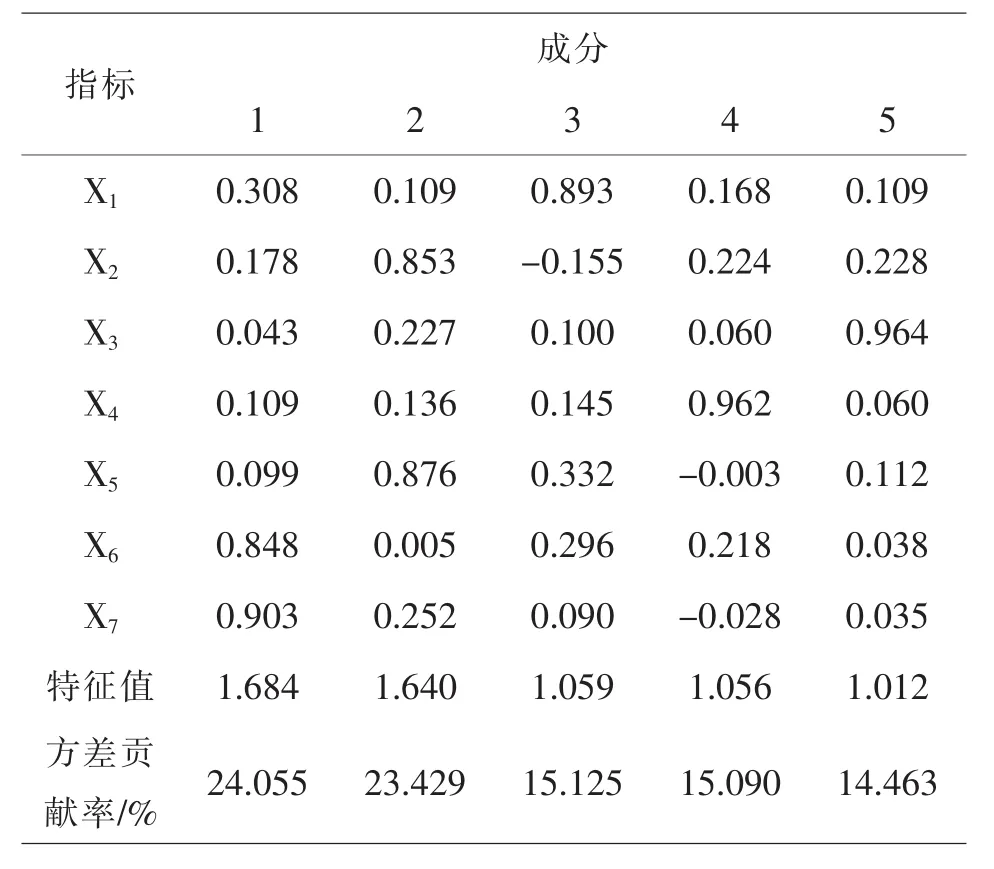
表2 因子正交后的旋转因子载荷矩阵

依据载荷系数较大的变量分为一组的原则，可以将指标分为 5 组，（X6，X7）（X2，X5）（X1）（X4）（X3）.由于第3、4、5组分别只有一个指标，因此只对1、2组进行主成分分析.用SPSS软件分别对1、2组进行主成分分析，并计算特征向量，得到结果如表3所示.由于各组的第一主成分均已达到80%以上，虽然没有达到85%，但已经比较接近提取标准，故每组只提取第一主成分[11].

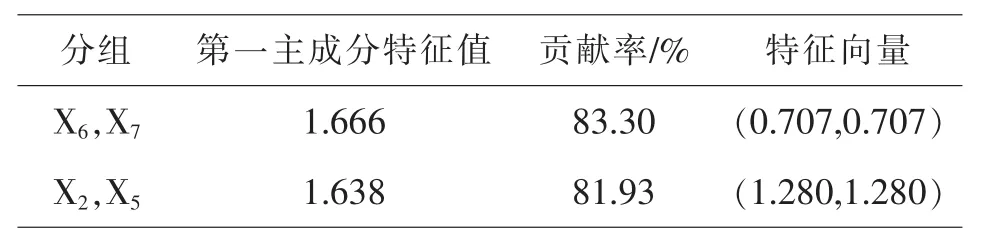
表3 分组主成分分析结果

根据表2和表3，即可构建大学生综合素质评价模型

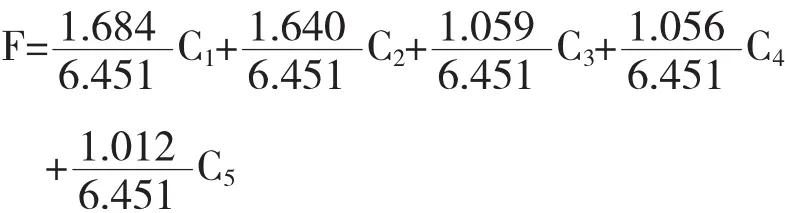
其中：C1=0.707X6+0.707X7，为“德育和能力”因子

C2=1.28X2+1.28X5，为“专业能力”因子得分

C3=X1，为“身心素质”因子得分

C4=X4，为“计算机能力”因子得分

C5=X3，为“外语能力”因子得分

2.2 学生综合素质测评结果分析

将标准化后的各项学生成绩数据代入大学生综合素质评价模型，即可得到如表4所示的学生综合素质测评各因子得分和综合素质测评总成绩.总体来看，学生综合素质测评各因子得分有正有负，大小不一，说明学生的各方面表现差异较大.得分越高说明学生在该因子上表现越好，在下一学年需继续保持，争取稳重求进.得分为负表明学生在该因子上表现较差，低于专业平均水平，需要改进学习方法，在该因子上重点加强.分别有37人、34人、29人、32人、28人在德育和能力因子、专业能力因子、身心素质因子、计算机能力因子、外语能力因子上得分为负.德育和能力因子得分为负的学生人数最多，与这两个班平时气氛不够活跃，参加活动不积极，获奖少且两极分化严重的事实十分吻合.有一半的学生专业能力因子得分为负，说明学风建设力度不够，理论课和实验课学习效果不好，学生对专业知识和技能的掌握还需进一步加强.将近一半的学生身心素质因子得分为负.由于多数学生的心理都是健康的，所以此项得分较低主要是缺乏锻炼，身体素质较差导致的.可以学校运动会、学院越野赛、拔河比赛以及团中央提议的“走下网络、走出宿舍、走向操场”三走活动为契机，鼓励学生积极参与，加强体育锻炼，提高身体素质.有29名学生计算机能力因子得分为负，可鼓励他们在学好计算机课程的基础上进一步提高计算机水平，考取计算机等级证书，为将来更好地就业增加筹码.有28人外语能力因子得分为负，相比其他因子人数较少，可见学院特色学风建设活动“领导带班晨读”以及校团委“四六级模拟考试”活动效果显著.仅有17号、26号、30号、41号、43号、57号6名学生各因子得分均为正，综合测评排名分别为第 2、5、1、14、11、4，表明他们在各方面发展均衡，综合能力处在专业前列.21号、28号、49号学生各因子得分均为负，应当深入了解实际情况并分析原因，有针对性地对其进行帮扶.

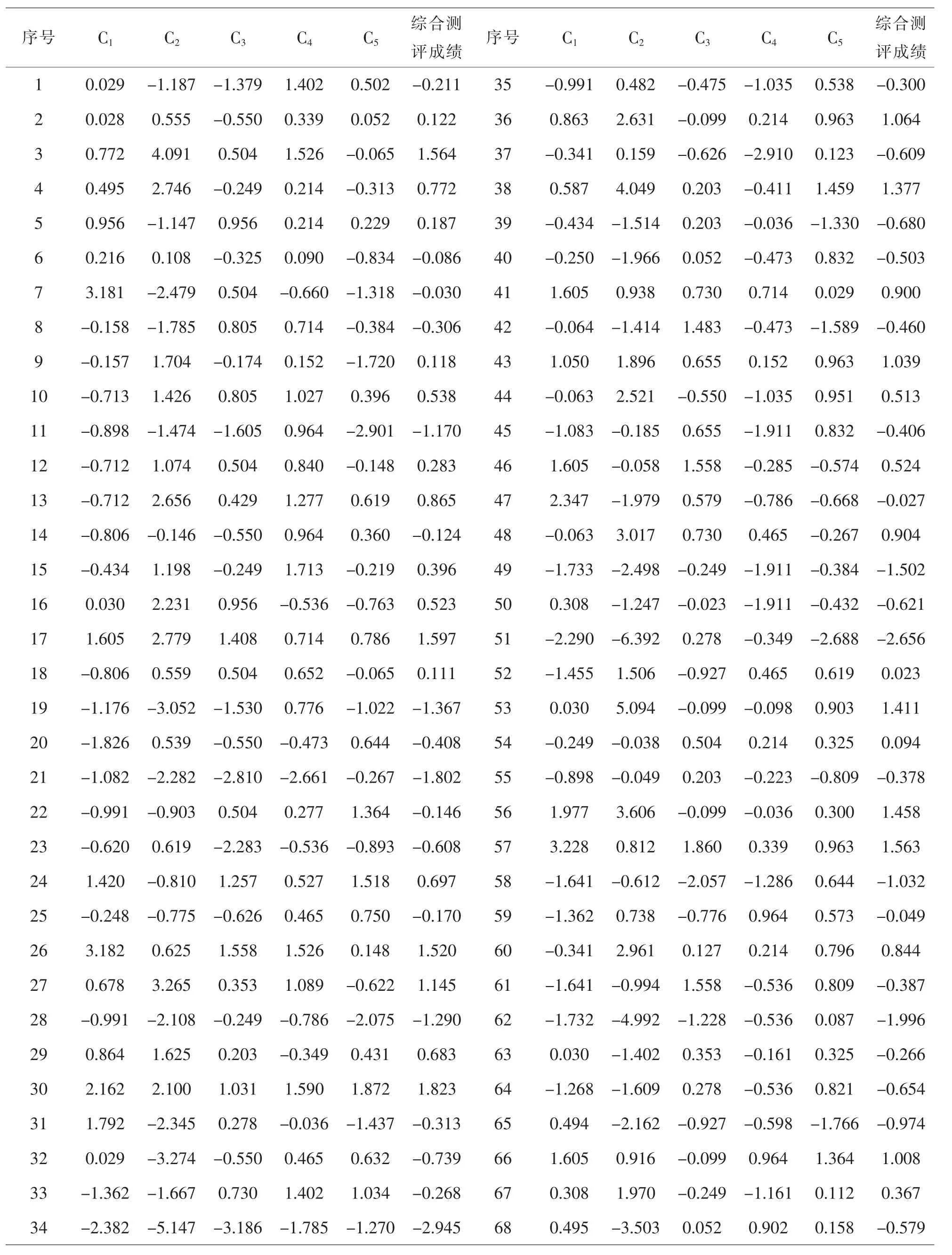
表4 学生综合素质测评各因子得分及总成绩

2.3 分组主成分分析法学生的综合测评与常规测评结果比较

学生的综合素质测评内容主要包括专业素质、德育素质和能力素质三个方面[12]，涉及学生的思想政治表现、课程成绩、所获荣誉情况、竞赛获奖情况、担任学生干部工作表现和违纪情况等多个指标.目前多数高校在对大学生综合素质测评成绩进行计算时直接把加权平均成绩和其他指标量化值简单相加[3].表5把基于分组主成分分析法的大学生综合素质测评排名与常规算法的排名进行了比较.可以看出，两种方法得到的排名结果差异很大.仅有 3、11、17、30、43、45、51 号 6 名学生的两种排名相同.其余62名学生均存在不同程度的差异，有3名学生的差异甚至高达18个名次，分别是33、47、67号.造成差异的主要原因是多个测评指标之间存在着信息重叠，直接相加导致测评结果出现偏差，不能科学、客观地反映学生的综合能力.分组主成分分析法能够在最大限度地保留原有信息的基础上，对多维变量进行综合降维处理[13-14]，将相关性较强的指标重新组合成一组新的互相无关的综合指标来代替原指标，有效地避免了常规算法中出现的信息重叠问题，提高了综合评价的科学性和合理性.

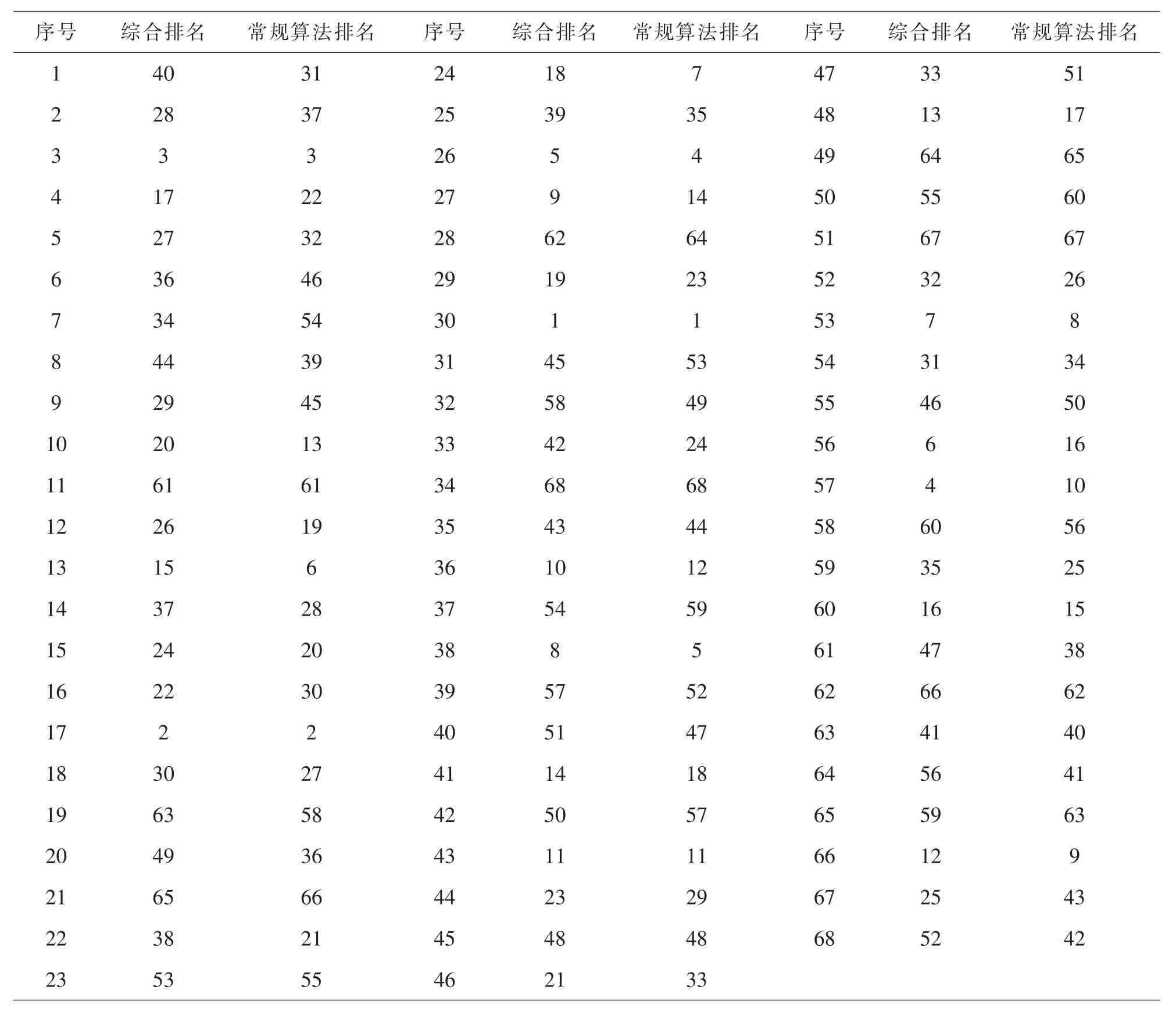
表5 分组主成分分析法与常规算法学生的综合测评排名比较

3 结论

采用分组主成分分析法构建评价模型，以商洛学院2015级食品科学与工程专业68名学生为例，对其2015—2016学年的综合素质测评成绩进行计算和分析，并与目前我国高校普遍使用的计算方法进行了比较.结果表明：两种算法得到的结果差异很大.相比常规算法，采用分组主成分分析法计算大学生的综合素质测评成绩有以下优点：计算精度更高，操作更方便，用SPSS软件即可完成数据处理工作；通过提取主成分并重新分组，克服了常规加和法中出现的各指标信息重叠问题，提高了测评结果的科学性、全面性和合理性；评定结果的公平性能够得到保障，得到的测评成绩和排名可作为评奖评优的依据；综合素质测评各因子得分能够清晰地反映出学生各方面的优势和劣势，可让学生明确努力方向，激发奋斗热情.也可为高校辅导员或班主任有针对性地开展教育和引导工作，帮助学生全面发展、提升综合素质提供有效参考.