隧道衬砌可靠指标的优化求解方法

龚彦峰， 陈文博， 房 倩

(1. 中铁第四勘察设计院集团有限公司， 湖北 武汉 430063； 2. 水下隧道技术湖北省工程实验室， 湖北 武汉 430063；3. 北京交通大学城市地下工程教育部重点实验室， 北京 100044)

0 引言

JC法是工程结构可靠度计算中最常用的方法，由Rackwitz和Fiessleer于20世纪70年代末提出，是以当量正态化考虑随机变量实际分布的可靠指标计算方法，之后被国际安全度联合委员会(JCSS)推荐采用[1]。吴世伟于1990年在《结构可靠度分析》[2]中对JC法的简化和改进算法做了详细说明； 1999年，徐军等[3]采用改进的JC法对具有高次非线性和复杂性的三维岩体强度准则进行可靠指标计算； 李典庆等[4]于2002年提出一种改进的JC法，解决了功能函数为线性时JC法不一定收敛的问题； 李继祥等[5]在李典庆等的基础上进一步改进了JC法的求解过程，使得计算精度和收敛速度得到提高。

JC法适用于随机变量为任意分布下结构可靠指标的求解，计算精度基本能够满足工程要求。我国GB 50068—2001《建筑结构可靠度设计统一标准》和Q/CR 9007—2014《铁路工程结构可靠度设计统一标准》均推荐JC法为工程结构可靠指标计算方法[1]。2015年，中国铁路总公司发布的Q/CR 9129—2015《铁路隧道极限状态法设计暂行规范》[6](简称《暂行规范》)也采用JC法对隧道结构可靠指标进行校准，并优化设计了表达式分项系数。以往JC法的应用和研究均针对单一且连续光滑的功能函数，然而，对于隧道素混凝土衬砌或钢筋混凝土衬砌，其极限状态的功能函数在空间上是分段、不光滑的，分别由抗裂与抗压极限状态、大偏心与小偏心极限状态的功能函数组合而成，不同衬砌的极限状态功能函数在空间上虽然连续但不光滑，且各段有其可行条件。JC法在迭代过程中不能对验算点位置有所限制，最终计算结果可能超出函数的可行域，因此，选取各段计算的可靠指标中的最小值作为结构可靠指标，也是不合理的。为解决该问题，喻渝等[7]以偏心距均值和受压区高度均值分别作为素混凝土和钢筋混凝土衬砌的极限状态功能函数选用的判据，但由于围岩物理力学参数、衬砌材料性能等的变异性，使得衬砌的受力状态具有不确定性，以偏心距或受压区统计量作为判据缺乏理论支撑，其严谨性和准确性存疑。

为了能够考虑功能函数分段性质及各段的约束条件，本文引入基于可靠指标几何意义的优化求解方法。该方法与JC法同源于二阶矩方法，其优点是能够通过约束函数限制解的可行域。近年来，优化算法的研究和应用已经十分成熟， 1991年，Liu等[8]采用梯度投影法、罚函数法、增广拉格朗日法、序列二次规划法等优化方法进行可靠指标的计算； 之后Powell法、遗传算法、粒子群算法、蚁群优化算法等相继应用到可靠指标的优化求解中，但其在约束条件上的优势并未受到重视。

本文对高速铁路隧道二次衬砌(下文中衬砌均指二次衬砌)承载能力极限状态各功能函数的约束条件进行整理，通过抽样计算得到衬砌力学响应的统计特征，分析隧道衬砌受力状态的统计特征，建立有约束的可靠指标优化求解模型，分别应用到素混凝土和钢筋混凝土衬砌，并与JC法进行比较。

1 功能函数可行域的判别

1.1 素混凝土衬砌的功能函数

素混凝土衬砌有抗裂和抗压2种极限状态。对于有抗裂要求的素混凝土矩形截面偏心受压构件，参考地面建筑结构的混凝土结构设计相关文献[9]，考虑裂缝出现瞬间受拉区混凝土的塑性特征，建立素混凝土矩形构件抗裂验算表达式； 20世纪90年代，原铁道部建设司工程建设科研项目通过大量强度试验，引入偏心影响系数α建立了素混凝土衬砌偏心抗压承载力验算表达式[10]。素混凝土衬砌的2种极限状态功能函数见式(1)—(2)。

(1)

(2)

式(1)—(2)中：γ为抵抗矩塑性影响系数；φ为构件纵向弯曲系数；ft为混凝土抗拉强度；b为截面宽度；h为截面高度；e0为轴力偏心距，e0=M/N，其中M为弯矩，N为轴力；α为轴向力偏心影响系数；fc为混凝土抗压强度。

根据素混凝土抗压、抗裂验算表达式，得到Ⅲb型素混凝土衬砌抗压、抗裂承载力随偏心距变化示意图(见图 1)。由图1可知： 当偏心距较小时，抗裂承载力呈现剧烈波动，但此时拉应力并不是混凝土破坏的因素，因此不需要抗裂验算； 当偏心距在0.2h附近，抗裂与抗压承载力接近，之后抗裂承载力逐渐下降且低于抗压承载力。

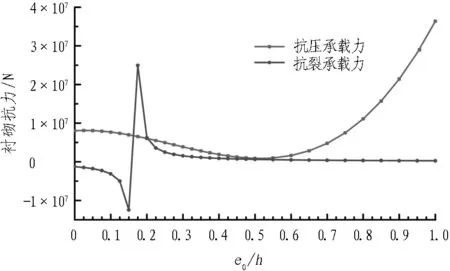
图1 素混凝土衬砌抗力变化曲线图

《暂行规范》[6]中规定： 仅当偏心距不小于0.2倍截面高度时，才进行抗裂验算。选取0.2h附近交点为临界偏心距e0*，则素混凝土衬砌的抗裂状态功能函数的约束条件为e0≥e0*，抗压状态功能函数的约束条件为e0≤e0*。

1.2 钢筋混凝土衬砌的功能函数

参考《暂行规范》[6],对钢筋混凝土衬砌的极限状态方程进行换算，消去相对受压区高度，以极限轴力、材料性能参数和截面几何参数表示钢筋混凝土衬砌功能函数，见式(3)—(4)。

(3)

(4)

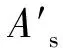
σs根据相对受压区高度分别取值，见式(5)。

(5)

式中：fy为钢筋抗拉强度；ξb为界限相对受压区高度；β1为等效矩形应力的高度系数； 3个参数都只与材料特性有关。

本文采用界限偏心距e0b来区分大小偏心极限状态，其依据与计算公式见文献[11]。钢筋混凝土衬砌的大、小偏心极限状态功能函数的约束条件分别为e0≥e0b、e0≤e0b。

2 隧道衬砌力学响应的统计分析

高速铁路隧道工程建设中对不同围岩条件、设计行车速度的双线隧道采取不同的二次衬砌设计参数，不同速度、围岩条件下衬砌结构和材料的类型见表1。

表1不同速度、围岩条件下的衬砌和材料类型

Table 1 Types of lining and materials under different speeds of train and surrounding rocks

速度/(km/h)围岩等级衬砌类型材料350、250ⅡⅡa、Ⅱb素混凝土ⅢⅢa、Ⅲb素混凝土ⅣⅣa、Ⅳb钢筋混凝土ⅤⅤa、Ⅴb钢筋混凝土

本文选取时速350 km高速铁路双线隧道Ⅲa型(二次衬砌为素混凝土结构，拱墙厚40 cm，仰拱厚50 cm)、Ⅳb型(二次衬砌为钢筋混凝土，拱墙厚45 cm，仰拱厚55 cm)衬砌，采用荷载-结构模型，参考相关研究对材料性能、围岩物理力学参数等的统计数据[7]，编制Monte-Carlo随机有限元计算程序。

从素混凝土和钢筋混凝土衬砌中，各选取从拱顶到仰拱中心的51个截面，对其力学响应特征进行统计，对以偏心距表示的受力状态进行分析，截面编号如图2所示。图3示出Ⅲa型衬砌拱顶处轴力、弯矩的均值和变异系数随抽样次数增加的变化趋势，当抽样次数达9 000 时，衬砌轴力和弯矩的均值和变异系数已经趋于稳定。经抽样发现，Ⅲa型和Ⅳb型衬砌各截面的力学响应特征均符合此规律，故确定随机抽样的样本容量为 9 000次。图 4(a)和4(b)分别示出Ⅲa型衬砌拱顶处轴力和弯矩的分布直方图、正态和对数正态分布拟合曲线及其拟合优度。由图4可知，正态和对数正态分布的拟合优度接近，并逼近于1，说明拟合效果均较好。考虑到计算的简便性和2种分布的特点，假定轴力和弯矩服从正态分布，其抽样置信水平为95%。

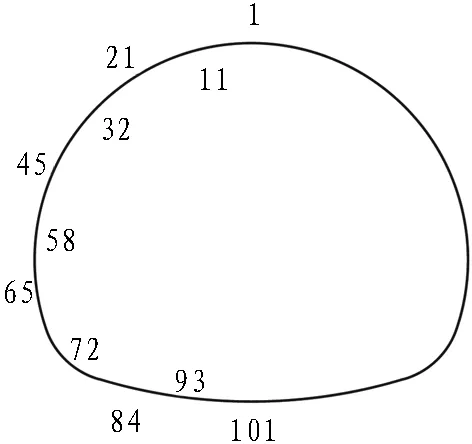
图2 衬砌单元编号示意图

图5示出Ⅲa、Ⅳb型衬砌截面偏心距平均值和变异系数随截面位置的变化曲线。由图5可知： 2种衬砌的偏心距均值及变异系数的变化趋势大致相同，从拱顶到拱底呈现波浪式变化，拱顶偏心距最大，其次为拱腰附近，Ⅳb型衬砌的偏心距均值稍大于Ⅲa型衬砌； 2种衬砌各截面偏心距的变异系数均低于5‰，基本分布在均值附近。各截面偏心距的低变异性表明了极限状态出现概率的两极分化，可以从侧面说明喻渝等[7]判别极限状态功能函数的方法具有一定的合理性，但缺乏对约束条件的明确表达，仍然不够严谨和准确。

3 可靠指标的优化求解

3.1 优化计算模型的建立

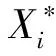
(6)

式中：σX为随机变量X的标准差；μX为随机变量X的均值。

(a) 轴力均值

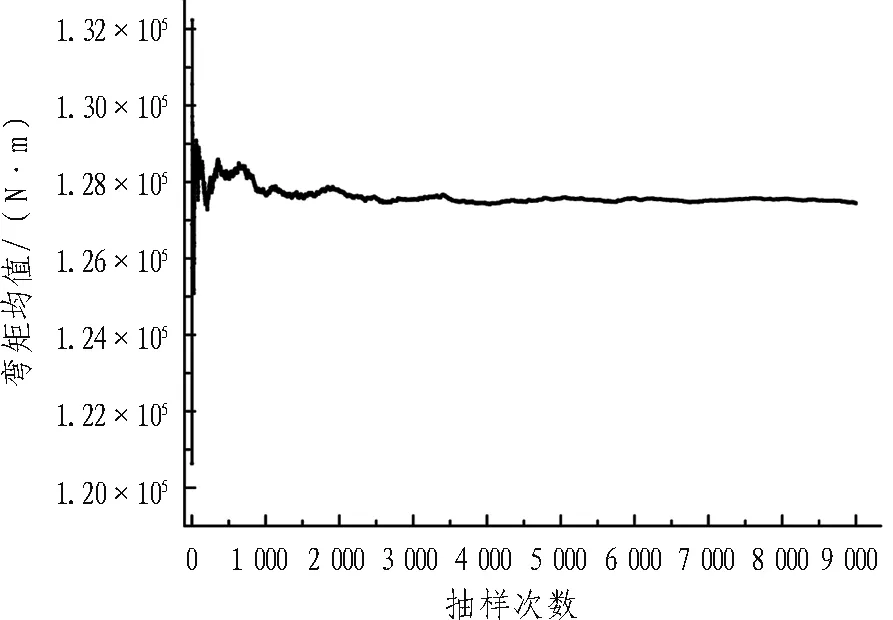
(b) 弯矩均值

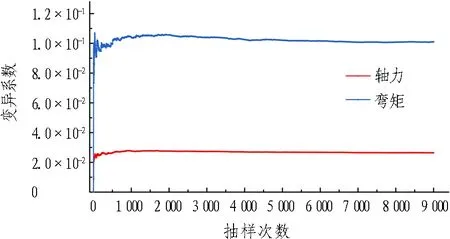
(c) 变异系数

Fig. 3 Variation curves of mean value of axial force and bending moment and coefficient of variation of lining of type Ⅲa

由结构可靠度理论可知，可靠指标的几何意义是：标准正态坐标空间中原点到极限状态曲面的最短距离[1]。根据材料强度参数、几何参数和抽样计算所得弯矩、轴力的分布类型与统计特征(均值、标准差)，通过坐标变换，可以将极限状态函数及其约束条件分别表示为优化求解模型中的等式约束与不等式约束，目标函数则为标准正态空间中功能函数曲面到原点的最小距离，如式(7)所示。

(7)

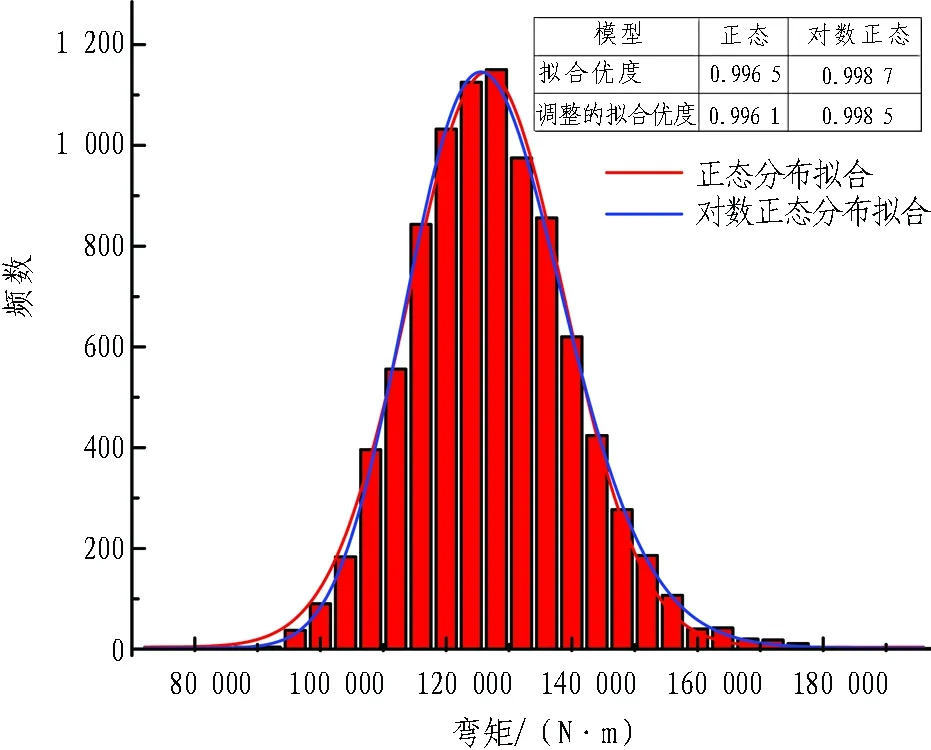
(b) 弯矩

Fig. 4 Distribution fitting of mechanical response of lining of type Ⅲa

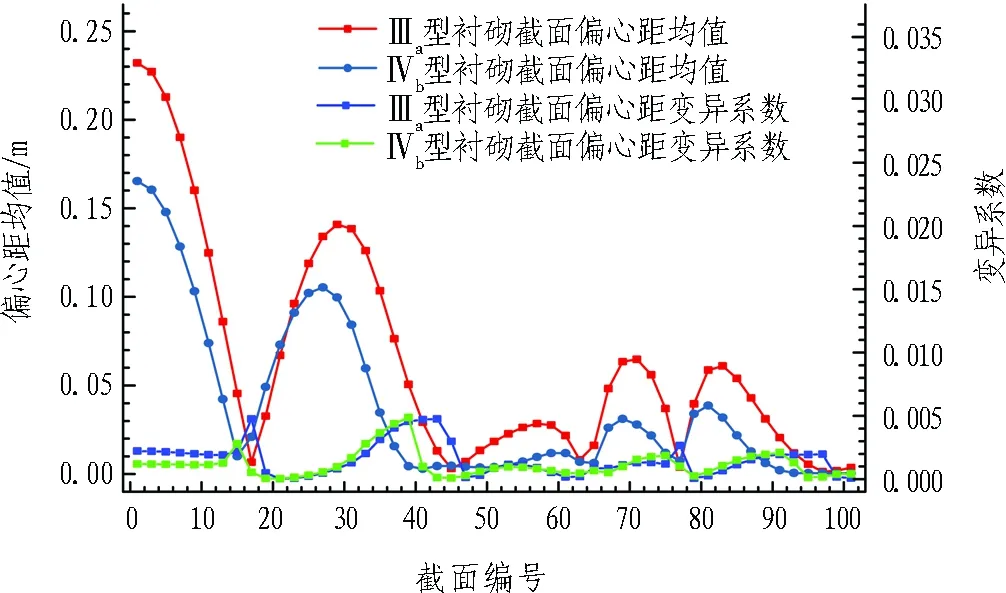
图5 Ⅲa、Ⅳb型衬砌截面偏心距平均值和变异系数变化曲线

Fig. 5 Variation curves of mean value and coefficient of variation of eccentricity of lining sections of type Ⅲaand Ⅳb

以钢筋混凝土衬砌为例说明优化方法相对于JC法的优点。图6示出钢筋混凝土衬砌大、小极限状态功能函数在轴力、弯矩空间的投影，其中AOB、COD分别对应大偏心和小偏心极限状态，仅AOD段代表实际极限状态，OB、OC段为无效段，界限偏心距e0b=cotα。当采用JC法计算可靠指标时，由于验算点在一个固定的功能函数上持续迭代，验算点位置有可能出现在OB、OC段，使得计算结果有误； 同时，采用JC法对2种极限状态计算得到的2个可靠指标，仍要验算其是否符合约束条件，过程复杂。优化求解方法则可通过约束条件将求解域限定在AO、OD段，所求最小值即为最终求解值，从而优化求解值也必将大于等于JC法迭代计算的最小值。

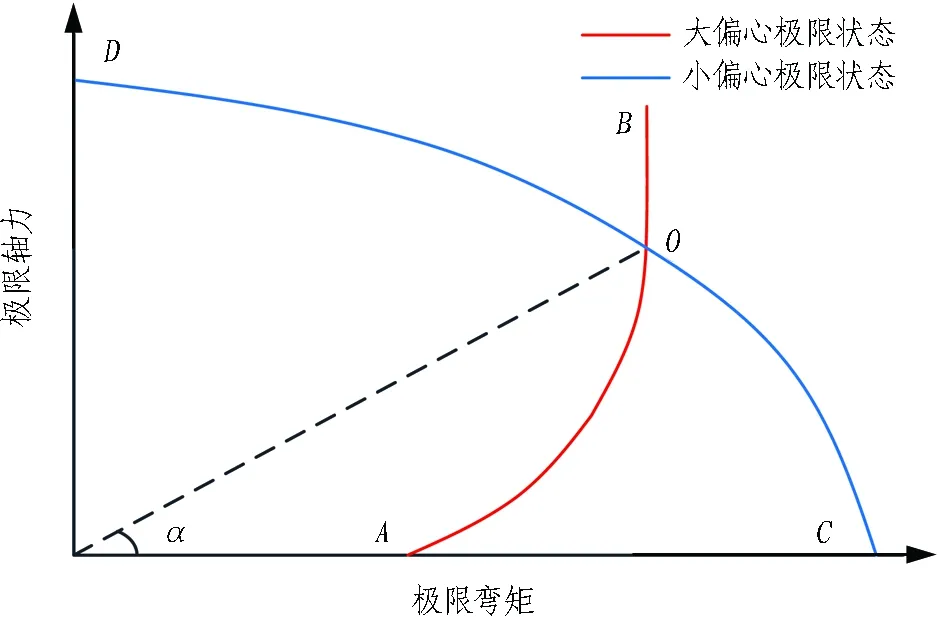
图6 功能函数空间示意图

3.2 素混凝土衬砌可靠指标计算

利用前面抽样计算得到的衬砌内力响应的统计特征和喻渝等[7]得出的C30混凝土衬砌厚度和混凝土抗压、抗拉强度的统计特征(见表2)，以弯矩、轴力、衬砌厚度和混凝土抗压、抗拉强度为随机变量，计算Ⅲa型衬砌各截面可靠指标。

表2衬砌性能与几何参数统计(C30)[7]

Table 2 Statistics of characteristics and geometric parameters of lining (C30)[7]

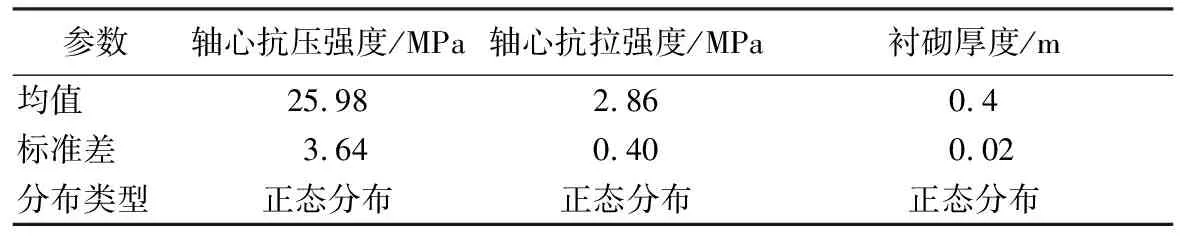
参数轴心抗压强度/MPa轴心抗拉强度/MPa衬砌厚度/m均值25.982.860.4标准差3.640.400.02分布类型正态分布正态分布正态分布

为测试优化算法性能，采用Matlab优化工具箱中的Global Search函数和JC法分别对素混凝土衬砌抗裂和抗压极限状态的可靠指标进行求解计算。Global Search是一种从基于分散搜索生成的试验点开始，分别进行搜索的全局最优化算法，适用于目标函数和约束函数均连续的优化问题。在算法测试中，对所有功能函数均不设置约束，求解目标均为可靠指标最小值。

素混凝土衬砌2种方法的可靠指标计算结果见图7，当偏心距较小时，抗裂承载力较小，采用JC 法计算的抗裂可靠指标为负值； 而优化求解计算的是验算点到原点的空间距离，为正值，因此两者会出现互为相反数的情况，本文取其绝对值进行比较。图7(a)中，Global Search函数优化求解值与JC法求解值完全重合； 图 7(b)中，JC法和Global Search函数求解值也完全重合，说明Global Search函数寻优性能良好，能够满足素混凝土的可靠指标求解。因此，采用Global Search函数对可靠指标进行优化求解(有约束)，并与 JC法求解值(无约束)作对比，结果如图8所示，Global Search优化值与JC法求解值分段重合。以上计算结果说明： 优化方法中功能函数约束条件的引入，解决了采用JC法时功能函数界限模糊、计算值难以区分的问题，实现了衬砌各截面可靠指标的准确求解。

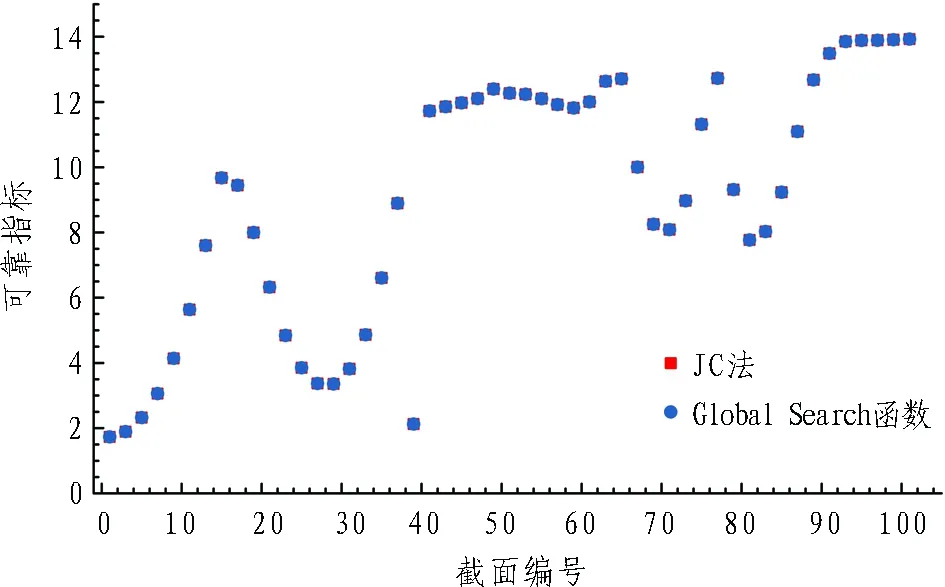
(a) 抗裂

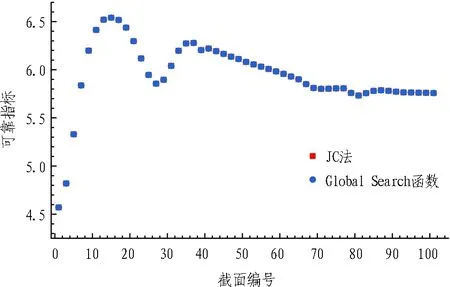
(b) 抗压

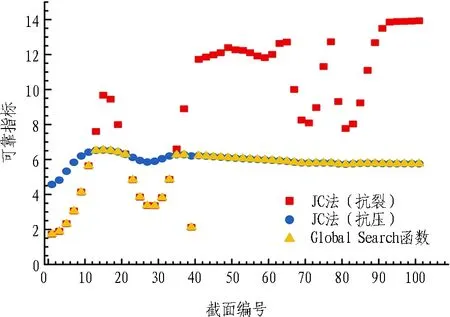
图8 素混凝土衬砌可靠指标优化求解计算结果

3.3 钢筋混凝土衬砌可靠指标计算

利用前面抽样计算得到的衬砌内力响应的统计特征和喻渝等[7]得出的C35混凝土衬砌厚度、混凝土抗压强度和钢筋抗拉强度的统计特征(见表3)，以弯矩、轴力、衬砌厚度、混凝土抗压强度和钢筋抗拉强度为随机变量，对Ⅳb型衬砌各截面可靠指标进行计算。

表3衬砌性能与几何参数统计(C35)[7]

Table 3 Statistics of characteristics and geometric parameters of lining (C35)[7]

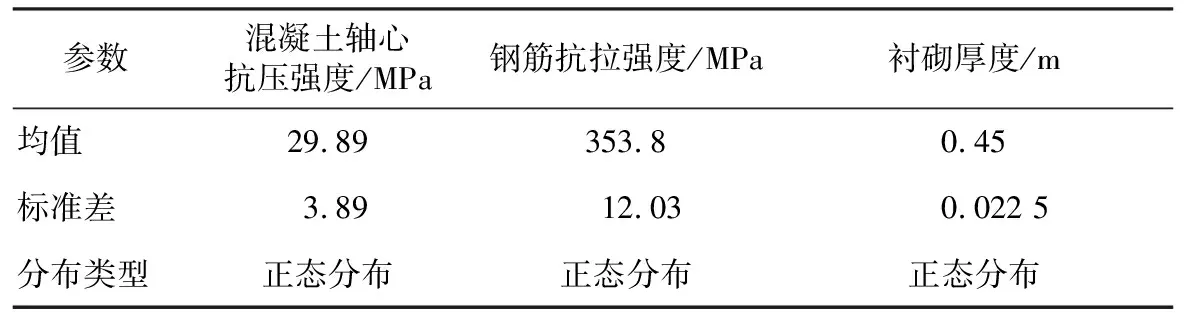
参数混凝土轴心抗压强度/MPa钢筋抗拉强度/MPa衬砌厚度/m均值29.89353.80.45标准差3.8912.030.022 5分布类型正态分布正态分布正态分布

同样采用Global Search函数和JC法分别对钢筋混凝土衬砌的可靠指标进行求解计算，结果如图9所示。由图 9可知： 对于2种功能函数，JC法和Global Search函数优化求解值完全重合。因此，钢筋混凝土衬砌的可靠指标优化仍选用Global Search函数。

(a) 小偏心状态

(b) 大偏心状态

Fig. 9 Comparison of calculation methods forRIof reinforced concrete lining

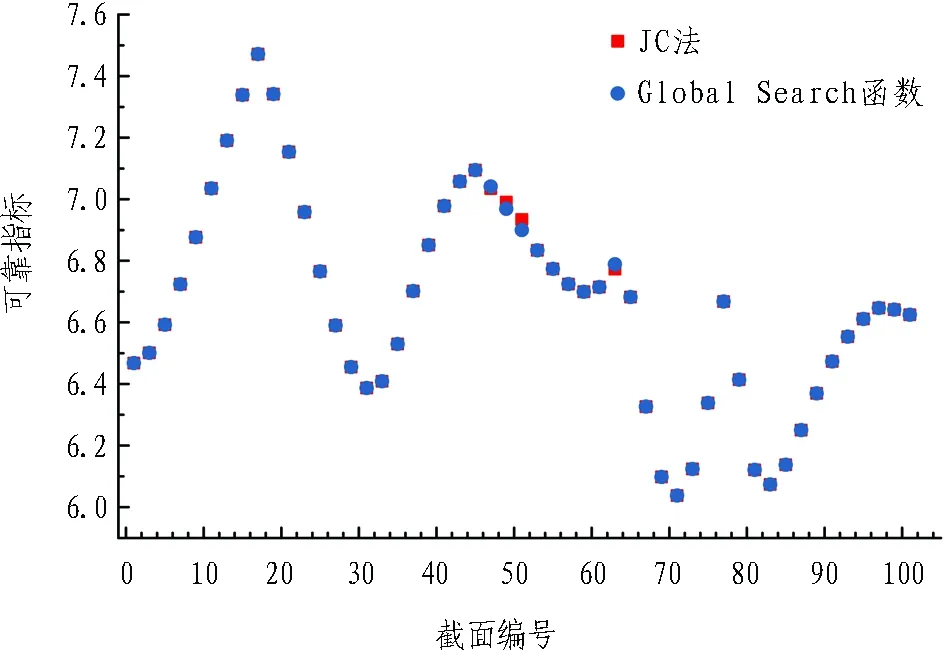
钢筋混凝土衬砌可靠指标优化求解计算结果如图10所示，由图10可知： 1—39号截面的优化求解结果与不同极限状态下的JC法计算结果分段重合； 40号截面之后的优化求解值与JC法计算值不重合，但不小于JC法计算的最小值。分析可得： 求解值重合是因为该处迭代终止点并未落在失效段，且可靠指标最小，优化法成功搜寻到最优解并与其重合； 不重合的原因是由于缺乏约束，JC法迭代终止点落在了失效段，JC法计算值始终为该功能函数所求的最小值，而优化法仅在可行域之内搜寻，故JC法计算最小值结果小于优化值。计算结果一方面表明考虑极限状态约束条件的优化求解方法在钢筋混凝土衬砌可靠指标计算中取得成功应用，另一方面也说明采用JC法分别计算2种极限状态的可靠指标，再取其中最小值的方法是不可取的。

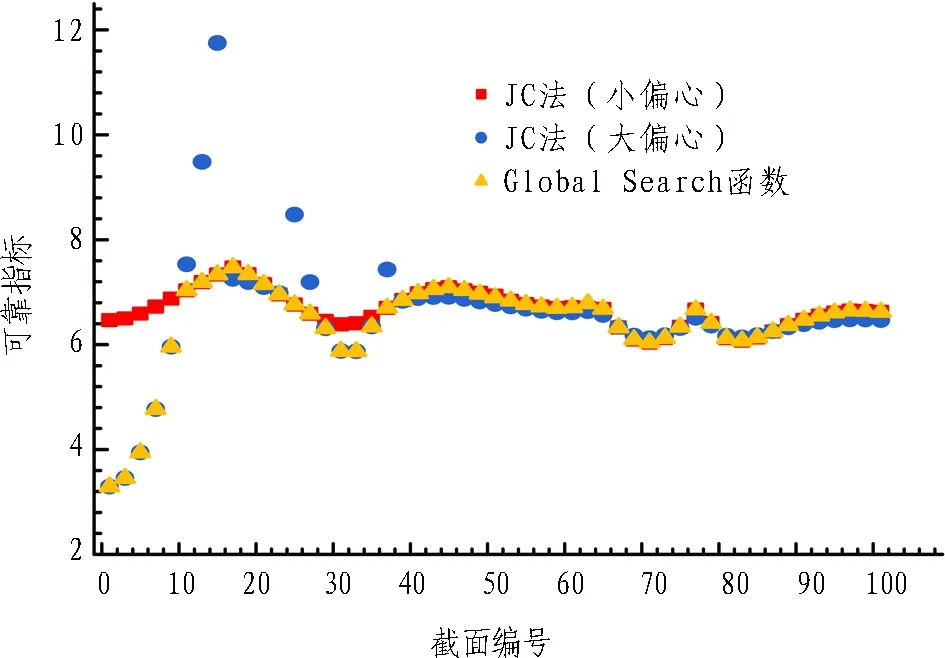
图10 钢筋混凝土衬砌可靠指标优化求解计算结果

Fig. 10 Optimization solution results forRIof reinforced concrete lining

4 结论与讨论

4.1 结论

本文通过采用随机有限元方法、Monte-Carlo抽样计算、优化函数的调用和对相关研究的归纳整理等手段，对隧道衬砌受力状态和可靠度计算方法进行研究，得到以下结论。

1)综合素混凝土衬砌和钢筋混凝土衬砌极限状态功能函数的相关研究，给出抗裂与抗压、大偏心与小偏心极限状态的判别条件。

2)对时速350 km双线隧道Ⅲa、Ⅳb衬砌进行抽样计算，考虑2类衬砌各截面偏心距的低变异性，分析目前可靠指标计算中极限状态功能函数选用方法的合理性及不足。

3)建立可靠指标的优化求解模型，证明了Global Search函数寻优性能较好，能够考虑各极限状态功能函数的适用条件，消除极限状态功能函数选取的模糊性，实现了对隧道衬砌各截面可靠指标的准确快速求解。

本文研究采用优化求解方法，解决了JC法求解隧道衬砌可靠指标中极限状态功能函数选取的问题，与目前采用偏心距或受压区高度均值的判别方法相比，更具有严谨性和便捷性； 同时，证明了用JC法分别计算2种极限状态然后取其最小值的不合理性。

4.2 存在问题及建议

隧道赋存于复杂的地质条件中，围岩参数及衬砌与围岩的相互作用模式具有高度的不确定性。本文采用荷载-结构模型和根据当前隧道规范提供的地层荷载计算方法，并未考虑计算模型的不确定性和围岩物理力学参数的空间变异性。此外，“单失效模式”的可靠性分析方法虽然被广泛采用，但对于隧道这种高次超静定结构，其评价指标过于单一，理论基础也不尽合理； 而对于隧道结构多失效模式的可靠指标计算(如点估计法、界限范围估计法等)，优化方法能够排除不同极限状态的干扰，无需进行极限状态判别和计算值的验算与比选，从而实现快速准确求解，适用性更强。

在当前的研究现状下，描述和考虑围岩物理力学参数及力学计算模型的不确定性，建立基于隧道-围岩体系的失效模式及可靠性评价体系仍是隧道可靠性研究的重点和难点。本文仅对可靠指标的计算方法进行部分改进，下一步应紧紧围绕以上几个基本问题，基于目前隧道失效模式、隧道与围岩相互作用关系及其不确定性描述的最新研究成果，发展隧道可靠性评价体系，进一步强化可靠性计算的手段与方法。