基于非线性模型的深水隔水管横向振动固有频率分析

郝逸，王文明,*，李皓冉，龚普，熊明皓，顾继俊

1 中国石油大学(北京)机械与储运学院， 北京 102249

2 南京晨光集团有限责任公司地面设备设计研究所，南京 210006

0 引言

隔水管是海洋钻修井作业的关键装备，其长度长、柔度大，易发生振动。随着作业深度增加，海洋载荷复杂多变，隔水管动力响应十分复杂，严重时会发生共振导致作业事故[1-2]，造成巨大的经济损失，甚至对作业人员生命安全和海洋环境造成威胁。随着国家深水战略的提出，对千米级隔水管作业要求愈发严格。因此，对隔水管固有特性开展研究十分重要[3-6]。

国内外学者对隔水管固有频率进行了大量理论和实验研究。Sparks C P[7]研究了隔水管横向模态振动的物理特性，提出了固有频率、节点和反节点位置、底部球绞的最大转角和隔水管最大弯曲位置的简化公式；刘清友等分析了钻井液的流速、顶张力和隔水管结构参数等对固有频率的影响[8]；畅元江等[9]基于能量守恒定律提出了隔水管固有频率的简化计算公式，其计算结果与相关文献[10]计算结果比较吻合；郭海燕等[11]利用有限元方法研究了内部流体流速和顶张力对隔水管固有频率的影响，结果表明内部流体流速越大，固有频率越小；韩春节等[12]采用微元法得到了隔水管数学模型，并利用分离变量法求解；邵卫东等[13]考虑浮体升沉及张紧环运动，提出了计算深水顶张力立管固有频率的方法。以上对隔水管固有频率的研究，忽略了隔水管轴向力沿长度的变化，主要利用有限元软件或者通过实验确定隔水管的固有频率。

论文采用微元法建立了隔水管横向振动力学模型，考虑轴向力变化，通过施加不同频率的外界激励引起隔水管系统共振，从而获得隔水管系统固有频率，利用有限差分法求解了隔水管非线性模型。基于隔水管非线性振动模型，分析了隔水管的管长、壁厚、顶部张力、附加质量和钻井液对隔水管固有频率的影响。

1 隔水管力学模型的建立

1.1 隔水管系统模型

隔水管系统建立力学模型，如图1所示。以海底井口正上方的海平面为坐标原点o，z轴正方向指向海底，海洋载荷沿着x轴作用在隔水管上，隔水管上端通过上挠性接头与海上平台连接，隔水管下端通过下挠性接头连接在海底井口防喷器组。由于海洋载荷(海流、海浪等)的作用，平台一般小范围偏离井口正上方，从而引起隔水管弯曲变形。隔水管受力复杂，在建立隔水管数学模型之前做如下两点假设：

(1)隔水管振动属于小变形问题；(2)隔水管是由均质、各向同性、线弹性材料制成的，管径一致，抗弯刚度沿水深不变。

1.2 隔水管微元受力分析

将隔水管划分为n段微元，取任一微元段ds做受力分析如图2所示。其中，隔水管单位长度受到的浮重为Fw、弯矩为M、轴向力Frt、剪力Frs、海洋载荷Fws和惯性力。

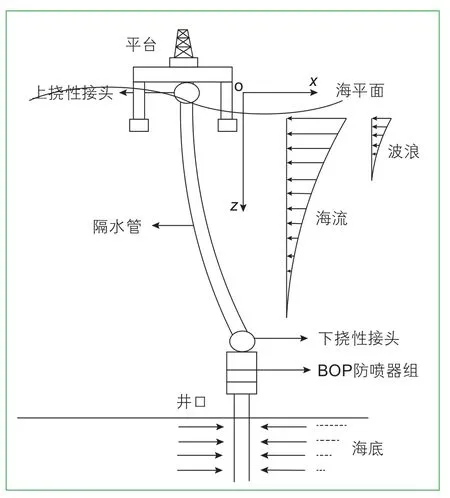
图1 隔水管系统模型Fig. 1 The riser model

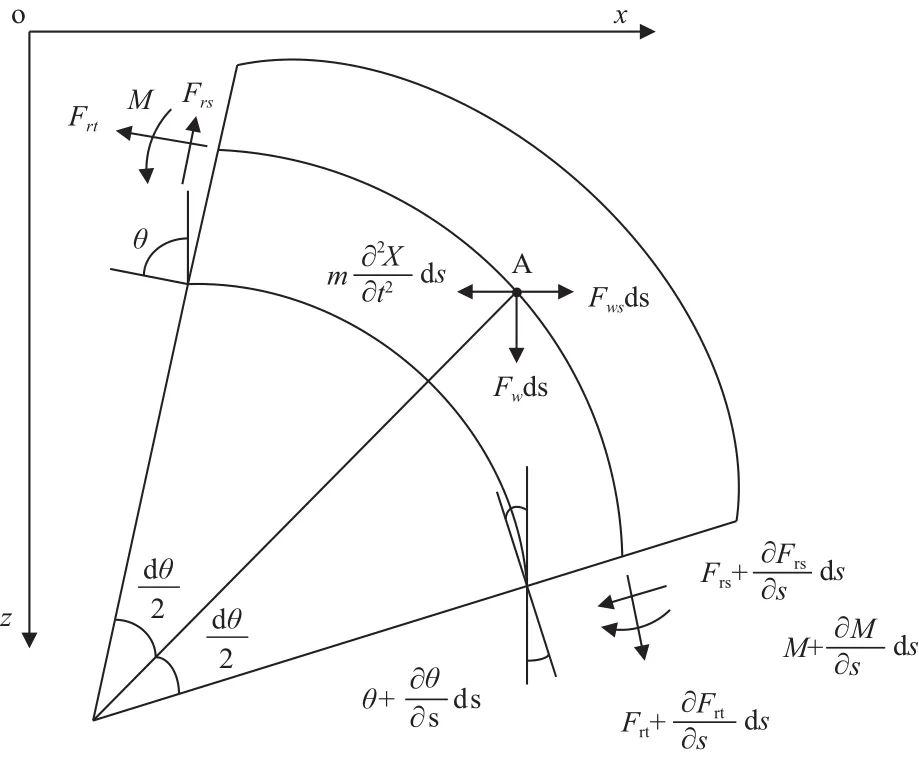
图2 隔水管微元受力分析Fig. 2 Analysis of riser microelement

对x方向受力分析：

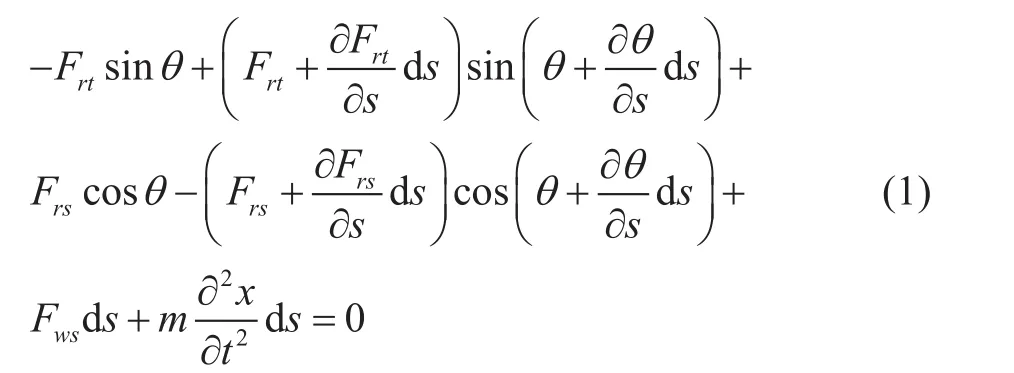
对z方向受力分析：

对A点取矩：

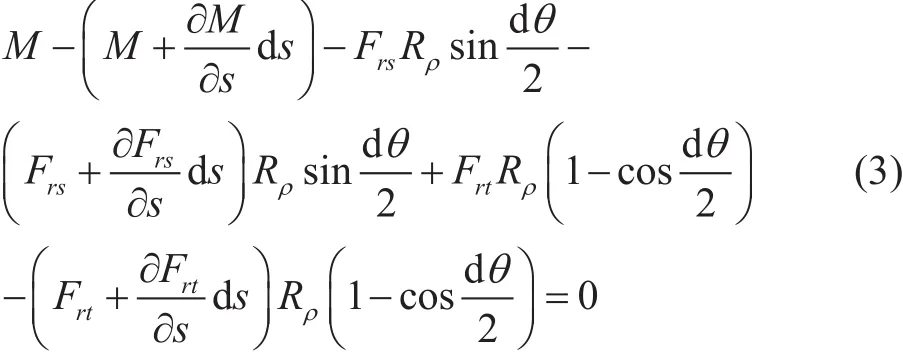
式中：Frt为隔水管微元段所受轴向力，N；Frs为隔水管微元段所受剪切力，N；m=mr+ma+ml，分别表示单位长度隔水管的重量、单位长度附加水质量和单位长度钻井液的质量；M是隔水管微元段所受弯矩，N·m；Fw是单位长度隔水管的浮重，N；Fws为单位长度隔水管所受海洋载荷，N；Rρ为隔水管微元段的曲率半径；θ是微元段横截面法线与z轴的夹角；是微元段横截面法线与z轴的夹角的变化量。

假设隔水管为等截面梁，则有：

式中：E为材料的弹性模量，Pa；I为截面惯性矩，m4。

将式(5)带入式(4)可得：

式(6)为剪力和弯矩关系，带入式(4)得隔水管横向振动控制方程：

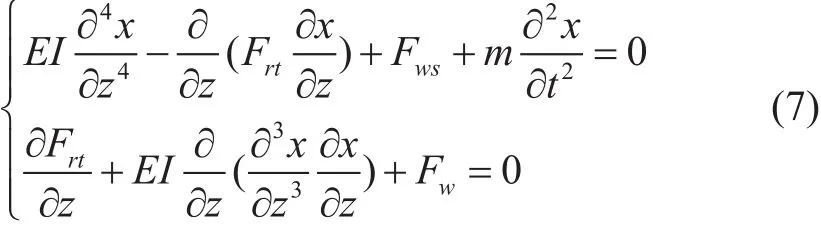
式(7)中已知量有：抗弯刚度EI，轴向力Frt，单位长度质量m，海洋载荷Fws，单位长度浮重Fw，任意一点的海洋深度z，未知量为x和Frt。

根据实际工况，隔水管的顶端和底端为铰接，则隔水管的转动刚度为0，下端位移为0，上端位移为常数，可得边界条件如式(8)所示。

其中：S为平台相对井口的水平偏移量，m。

对隔水管横向振动的研究都是基于对(7)式的求解，然而方程高度非线性，无法直接表示轴向力Frt。国外内研究通常假设隔水管轴向力沿着海洋深度不变或者线性变化，本文探讨采用非线性模型对该问题进行求解。

2 非线性模型求解

2.1 假设模型

(1)线性模型：认为轴向力Frt为恒定不变，隔水管任意位置的轴向力为整段隔水管浮重的1.2～1.6倍。顶张力系数取1.2，因此隔水管横向振动控制方程变为下式：

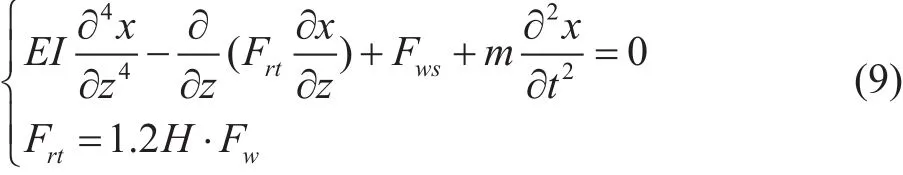
其中：H为海洋深度。

(2)非线性模型：考虑隔水管质量，认为轴向力Frt随海洋深度线性变化，隔水管顶部张紧力为整段隔水管浮重的1.2～1.6倍。因此隔水管横向振动控制方程变为式(10)：

其中：F0为隔水管顶部张紧力，顶张力系数取1.2。

非线性模型的顶张力系数取1.2，故轴向力为：F（rtz , t） = 1 .2HFw- Fwz ， 带 入 横 向 振 动 方 程 式 得 式(11)。

式(11)为非线性偏微分方程，需采用数值解法求解。为求得固有频率，假设对隔水管在沿管长方向均匀施加外部激励Fws(z, t) = fwseiϖt，选取不同的激励频率，当隔水管的固有频率和外部激励频率相近时，就会发生共振，幅值会无限大，确定隔水管的固有频率[13]。

假 设 立 管 的 稳 态 振 动 形 态 为x( z, t) = xˆ( z, ϖ )eiϖt，将外部激励和振动形态带入式(11)将偏微分转化为常微分得：

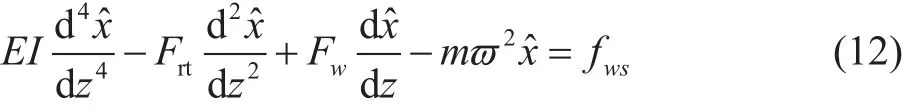
用中心差分公式代替微分[14]，带入式(12)，得到离散化方程，如式(13)，其中i=1,2,3…n。

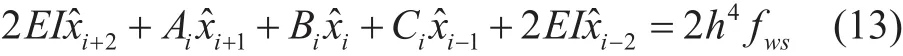
上式一共有n个方程，但是有x-1～xn+2共n+4个未知数，为此引入4个边界条件，并对边界条件进行差分[15]，得4个附加方程：

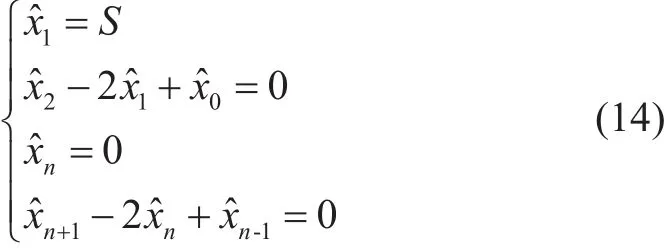
其中：S为浮体偏移，m。

式(13)与式(14)联合得到大型带状方程，利用Matlab软件编程求解。

2.2 算例

假设作业水深为1000 m，隔水管计算参数如表1所示。

非线性模型的固有频率通过共振法求解，通过对系统施加不同频率的外部激励，引发系统共振，间接求得固有频率。对整个隔水管施加0～2 rad/s的激励，隔水管在水下300 m、500 m和800 m 3个位置的位移如图3所示。

图3横轴代表外界载荷激励频率的变化，纵轴表示振动位移。在图3中，隔水管在300 m、500 m和800 m的位移都在特定激励频率作用下同时达到无限大，这些特定激励频率引起了隔水管的共振，由图3可得非线性模型前十阶固有频率如表2所示。

2.3 非线性模型求解精度分析

为了验证非线性模型求解结果的准确性，利用有限元分析软件ABAQUS提取隔水管前十阶固有频率，其中隔水管选取B21梁单元，划分为1000个单元，隔水管底部x、z方向和顶部x方向固定[18]，施加重力、浮力和顶张力，在频率提取分析步考虑附加质量，计算结果汇总在表3中。

为了对比非线性模型求解精度，与已有参考文献的求解结果公式进行对比。文献[16]给出固有频率计算简化公式如下，其前十阶计算结果见表3，

其中：Tl是隔水管顶端张紧力，N；Tb是隔水管底端张紧力，N。

文献[8]给出固有频率的简化计算公式如下，相比式(16)，考虑了抗弯刚度的影响，其前十阶计算结果见表3，

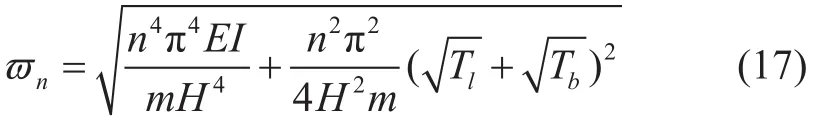
线性模型利用分离变量法即可求解[12]，其前十阶计算结果如表3所示。

采用不同计算方法得到的固有频率如图4所示。可以看出，非线性模型求解的固有频率整体小于线性模型，并且随着阶数升高，线性模型和非线性模型的差距越来越大。线性模型和非线性模型的一阶频率差0.060 rad/s，十阶频率差0.498 rad/s。原因在于线性模型假设隔水管各个位置轴向力为常数，没有考虑重力对轴向力的影响。

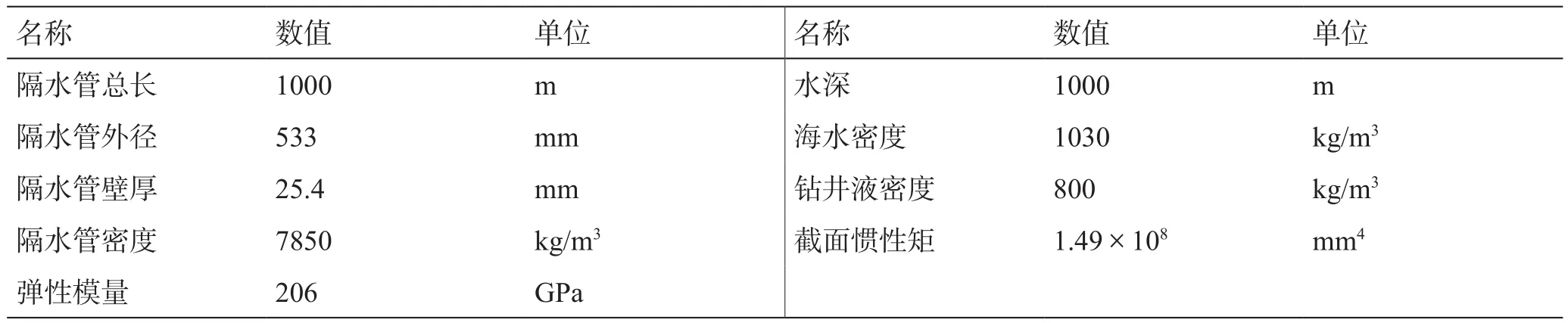
表1 算例参数Table 1 Examples parameters

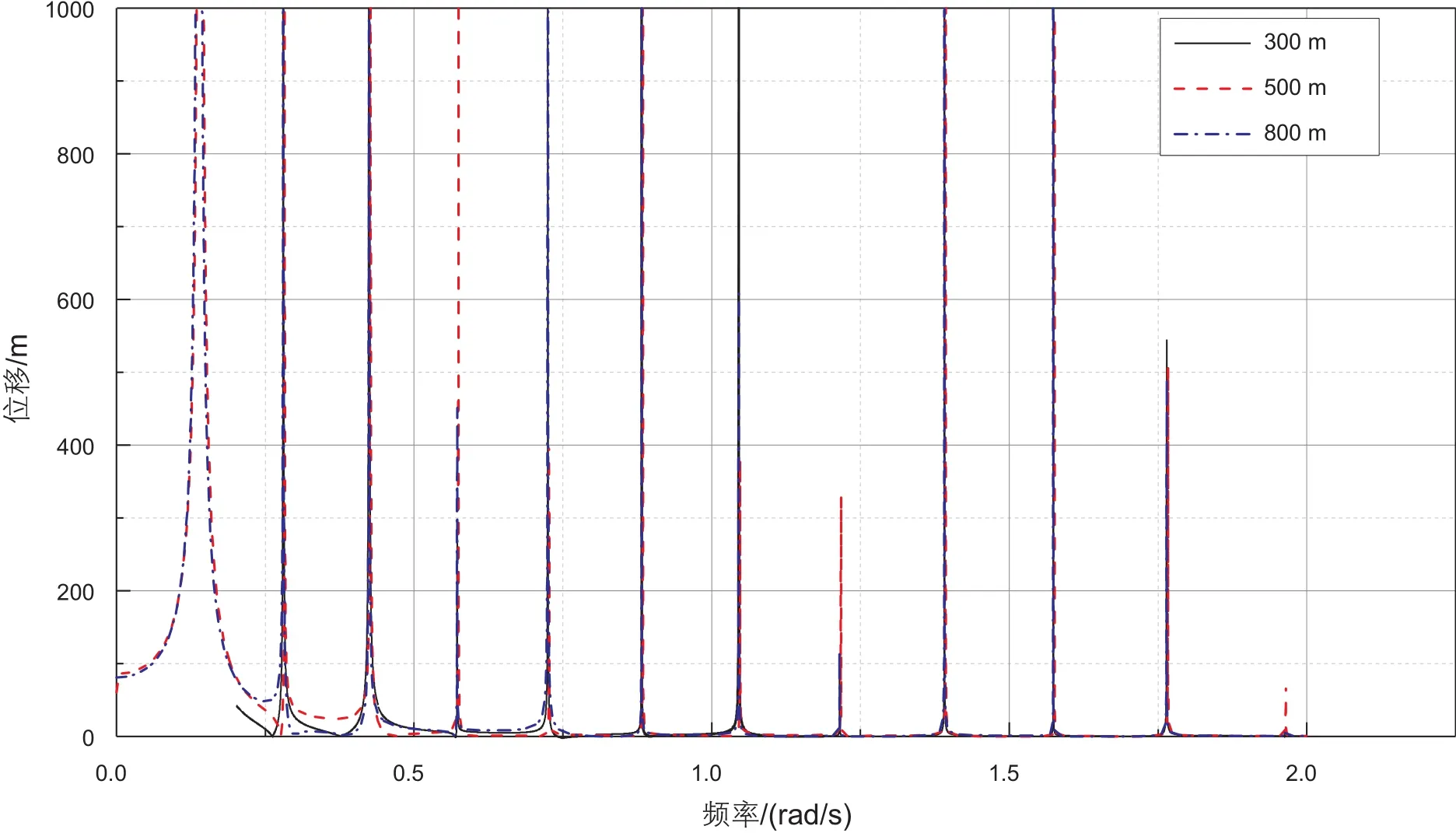
图3 不同位置的位移图Fig. 3 Displacement in different positions

表2 非线性模型前十阶固有频率Table 2 The natural frequency of nonlinear model

表3 有限元仿真、线性模型、文献[16]、文献[8]计算的前十阶固有频率Table 3 natural frequency by different methods

非线性模型与仿真结果相比，频率差值很小，虽然随着阶数升高，两者频率差逐渐增大，但十阶频率的差值也只有0.0147 rad/s，证明非线性模型计算结果准确性较高。

非线性模型与文献[16]在低阶固有频率的结果比较接近，一阶频率差只有0.0009 rad/s。但随着阶数升高，差值明显增大，十阶频率相差达到0.1802 rad/s。非线性模型与文献[8]的差值较小，十阶频率相差为0.0506 rad/s，可以看出非线性模型的求解精度更高。

综上可知，非线性模型考虑轴向力的变化，符合实际作业情况，结果对比分析也证明，非线性模型准确性较高。对隔水管的振动分析，应优先采用非线性模型。

3 隔水管固有频率的影响因素

影响隔水管固有频率的因素有外在因素和内在因素，外在因素主要是顶部张力、附加质量和钻井液；内在因素主要是管长和壁厚。论文在探究各因素对隔水管固有频率影响时，均以非线性模型进行计算。

3.1 顶张力对固有频率的影响

隔水管的长度、直径、壁厚和钻井液等因素假设不变，分析顶张力对固有频率的影响。隔水管顶部张力会影响隔水管的刚度，从而对固有频率产生较大影响。隔水管顶部张力一般为浮重的1.2～1.6倍，取浮重的1.2倍、1.4倍和1.6倍进行分析，计算结果如图5所示。

由图5可以看出，随着顶张力增大，隔水管各阶固有频率整体增大。针对海洋环境的复杂多变性，可通过调整隔水管顶部张紧力的大小改变系统特性[17]。

3.2 附加质量对固有频率的影响

图4 采用不同计算方法得到固有频率Fig. 4 Using different methods to get the natural frequency

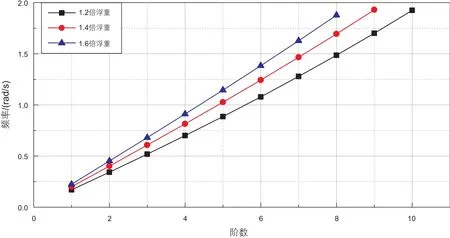
图5 顶部张力对固有频率的影响Fig. 5 The effect of top tension on natural frequency

海洋载荷会迫使隔水管振动，对管柱周围的流体做功，使管柱周围流体速度发生变化。计算时一般将其等效为附加质量，单位长度附加质量如式(18)所示。

式中：Cm为附加质量系数，取1；D为隔水管外径，m；ρw为海水密度，kg/m3。

假设隔水管的长度、直径、壁厚、钻井液和顶部张紧力等因素不变，分析附加质量对固有频率的影响，计算结果如图6所示。

由图6可以看出。模型考虑海水作用时计算的频率要比不考虑海水作用的整体偏低，并且随着阶数升高其频率差值呈增大趋势，十阶频率的数值相差最大为 0.351 rad/s。因此，计算时必须考虑由水动力引起的附加质量。

3.3 钻井液对固有频率的影响

隔水管作业时内部会充满钻井液，选取钻井液密度为 800 kg/m3、1000 kg/m3、1200 kg/m3和不考虑钻井液4种情况。计算时不考虑钻井液的流动，假设隔水管的长度、直径、壁厚和顶部张紧力等因素不变，计算结果如图7所示。

由图7可以看出，与不考虑钻井液相比，考虑钻井液计算得到的固有频率明显偏大，但随钻井液密度增大，隔水管固有频率仅略微升高。对比不考虑钻井液与隔水管内部充满1000 kg/m3的钻井液，其十阶频率相差达0.7346 rad/s。因此，计算时需考虑钻井液的影响。

3.4 隔水管管长对固有频率的影响

假设隔水管直径、壁厚、内部钻井液和顶部张紧力等因素不变，选取1000 m、1200 m和1500 m 3种管长。隔水管管长越长，隔水管柔度越大，计算结果如图8所示。

由图8可得，随着管长增大，隔水管频率整体降低，虽然在前三阶变化并不明显。但随着阶数升高，频率相差越来越大，长度1000 m 和1500 m隔水管的十阶频率相差达到0.469 rad/s。

3.5 隔水管壁厚对固有频率的影响

从式(19)中可以看出，隔水管壁厚增加，会使得隔水管的截面惯性矩增大，从而影响结构的抗弯刚度，

式中：D为隔水管外径，m，d为隔水管内径，m。

为了探究壁厚对固有频率的影响，选取25.4 mm、31.8 mm和50.8 mm 3种壁厚，假设隔水管长度、直径、内部钻井液和顶张力等因素不变，计算结果如图9所示。

由图9可得，壁厚越大，各阶固有频率越高。虽然在前几阶变化不显著，但随着阶数升高，频率差值明显增大。壁厚25.4 mm和50.8 mm的隔水管在九阶频率差为0.247 rad/s。

图6 附加质量对固有频率的影响Fig. 6 The effect of additional mass on natural frequency

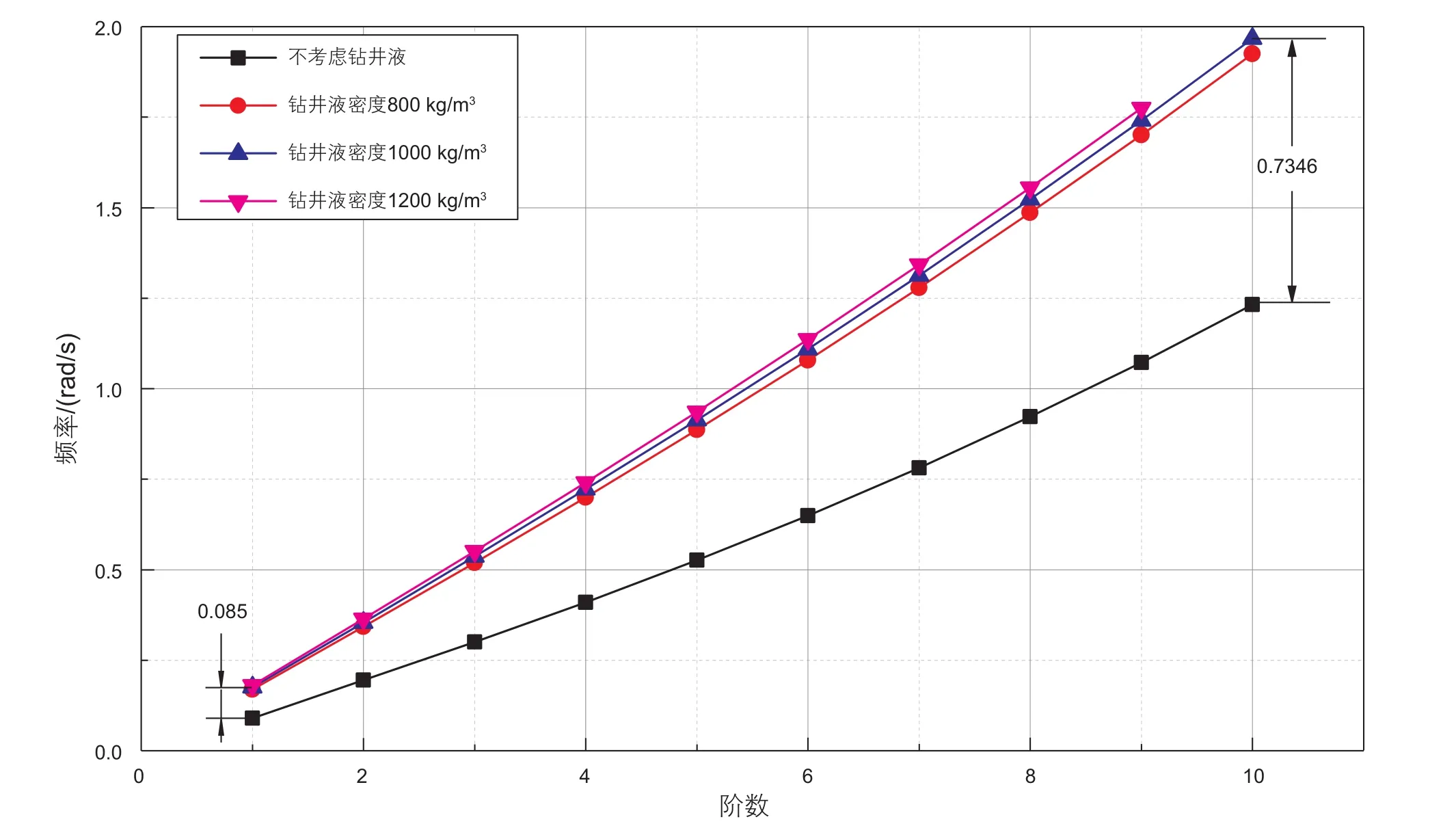
图7 钻井液对固有频率的影响Fig. 7 The effect of drilling fluid on natural frequency

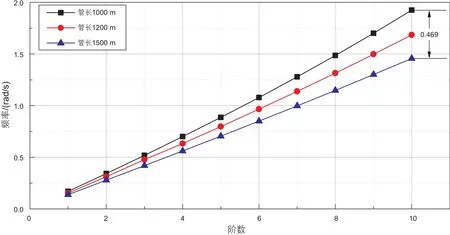
图8 管长对固有频率的影响Fig. 8 The effect of pipe length on natural frequency

4 结论

通过以上分析，得到的结论如下：

(1)利用微元法构建了隔水管横向振动控制方程，假设隔水管轴向力沿着深度方向线性变化，得到了非线性模型，能够较真实地简化实际工况。

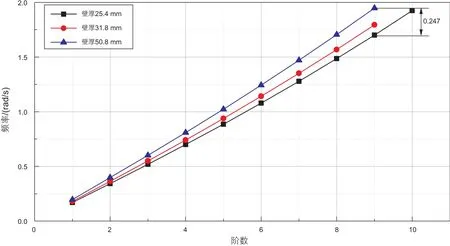
图9 壁厚对固有频率的影响Fig. 9 The effect of wall thickness on natural frequency

(2)利用共振法求解得到了隔水管的各阶固有频率，与有限元仿真结果、参考文献结果、线性模型结果进行对比，验证了非线性模型的准确性。

(3)分析了隔水管管长、壁厚、顶部张力、钻井液和附加质量对固有频率的影响。随着隔水管壁厚和顶部张力增加，隔水管固有频率增高；随着隔水管管长增大，隔水管固有频率降低；固有频率计算时需考虑附加质量和钻井液的影响，但钻井液密度大小对固有频率影响较小。