具有倾斜极化层的自旋阀结构中磁翻转以及磁振荡模式的微磁模拟∗
2018-09-21吕刚张红侯志伟
吕刚 张红 侯志伟
1)(山东农业大学信息科学与工程学院,泰安 271018)2)(河南工业大学物理系,郑州 450001)(2018年5月13日收到;2018年6月5日收到修改稿)
1 引 言
近期的研究表明,具有垂直磁各向异性(PMA)的自旋转移矩纳米柱结构具有良好的磁热稳定性、翻转临界电流低、受样品边比尺寸影响小等优点[1−5].因此,垂直磁各向异性材料在非易失性磁性存储器[6]与自旋转矩振荡器[7]领域有着广泛的应用前景.一种比较典型的优化结构为:自由层磁矩具有垂直磁各向异性,而极化层具有倾斜的垂直磁各向异性[8].倾斜的极化层磁矩在面内(in-plane,IP)及面外(out-of-plane,OP)均有分量,这为调控磁矩的动力学行为提供了一种新方法,可用来优化微波信号、增强自旋转矩效率以及调控静态与动态的磁模式[8−10]等.近期,一种具有IP和OP分量的双自旋极化层的结构模型已被提出[11−16].在这种器件中,PMA起到了非常重要的作用[17−19].已有研究表明,自旋霍尔效应与Dzyaloshinskii-Moriya相互作用(DMI)可诱导磁畴壁(DW)的有效传播[20−23],这使得具有PMA的材料在基于磁畴壁的信息存储器件方面有了一定的发展前景.此外,在具有较强垂直磁各向异性的纳米接触点中,自旋转矩作用还可以驱动固定在局域内的自旋波[24−27].
基于由(Co/Ni)材料构成的具有PMA的自旋纳米柱结构,我们已经研究了小角度倾斜的磁场、倾斜的自由层磁矩以及倾斜的极化层磁矩等降低的对称性对自由层磁矩磁化翻转曲线的影响.在自由层磁矩垂直膜面方向的分量平均值〈mz〉随磁场演化的进动曲线中,我们观察到一个明显的“凹槽”出现在低磁场区域[28].为了进一步澄清凹槽出现的物理机制以及该区域内自由层磁矩的动力学特性,我们做了进一步的微磁模拟研究工作.本文主要介绍具有垂直磁各向异性的椭圆形多层膜纳米柱结构中“凹槽”的物理机理.
2 研究模型与方法
模拟中,采用了自由层磁矩与极化层磁矩均为垂直磁各向异性的多层膜结构,其中极化层磁矩向面内方向倾斜3°.样品结构面内形状为椭圆形,尺度为50 nm×200 nm,自由层厚度为1.6 nm.微磁模拟研究基于模拟软件MuMAX3[29]采用有限差分法展开.自由层磁矩的动力学行为通过基于Landau-Lifshitz-Gilbert-Slonczewski(LLGS)方程的微磁模拟来研究[29−31].
在模拟中,电子从极化层流向自由层的方向定义为正向电流.材料的饱和磁化强度Ms=6.5×105A/m3,交换常数A=1.6×10−11J/m,各向异性常数K=2.5×105J/m3,自旋极化率为0.28.模拟样品被离散为一系列尺度为2.0 nm×2.0 nm×1.6 nm的单元格.初始平衡态下,自由层磁矩沿垂直膜面方向的 +z轴,而极化层磁矩偏离+z轴向面内长轴方向倾斜一个小角度3°.外加磁场的方向沿着−z方向,可驱动自由层磁矩偏离 +z方向翻转至−z方向.而正向的极化电流产生的自旋转矩作用将抑制自由层磁矩的翻转.
3 自由层中磁矩翻转与磁振荡的微磁模拟
图1(a)展示了自由层磁矩z轴分量的平均值〈mz〉在不同电流下与外加磁场的演化关系.我们注意到,在翻转曲线中出现了三个明显的“凹槽”区域,分别对应三个固定的磁场区域:−80 mT<µ0H<0 mT,−310 mT<µ0H< −250 mT以及−400 mT<µ0H<−340 mT.凹槽的出现可能来源于自旋转矩(STT)、各向异性场以及外加磁场之间的竞争.较小的应用电流下,例如I=0.3 mA,I=0.5 mA,相对较小的外加磁场即可驱动磁矩转向面内,而STT会抑制磁矩转向面内的进动.初始阶段,由于自由层与极化层磁矩夹角非常小,外加磁场产生的移矩作用强于STT,从而导致自由层磁矩随着磁场增强而逐渐倾斜.当自由层与极化层磁矩夹角增加到一定数值时,增强的STT作用以及各向异性场产生的移矩作用将克服外磁场的移矩作用并驱动磁矩回到初始位置,这导致了−80 mT<µ0H<0 mT区域内凹槽的出现.应用电流较大时,需要较强的外加磁场才可驱动磁矩偏离+z方向,这导致了另外两个凹槽的出现.在一定电流范围内,凹槽出现的位置不受电流大小的影响.
由于STT、各向异性场、外加磁场之间非稳定的平衡竞争,可导致凹槽区域多种磁振荡模式的出现.模拟结果显示,在不同的凹槽区域内自由层磁矩的磁振荡模式是不同的,但同一个凹槽区域内的磁振荡模式是类似的.图1(b)展示了−80 mT<µ0H<0 mT区域内−20 mT磁场下不同电流对应的〈mz〉随时间的振荡曲线,均为周期性振荡.对应图1(b),通过快速傅里叶变换我们给出了相应的频谱图,见图1(c).我们注意到随着电流的增加,主频峰的幅度在减小,这来源于增强的自旋转矩作用引起的〈mz〉振荡幅度减小(图1(b)).而随着电流的增加,频率值出现了蓝移.模拟结果显示,频谱图中最高峰对应的主频率值与自由层磁矩的进动频率相近.具有面内与面外双极化层的自旋阀结构中,自由层磁矩的周期性进动频率

式中γ为旋磁比,ħ为普朗克常数,Pop为垂直于自由层的极化分量,|J|为电流密度,α为阻尼因子,e为电子质量,l为自由层薄膜厚度[16].进动频率与面内极化层的自旋转矩作用无关.可以用该模型定性地解释频谱中出现的频率蓝移.而由于自旋转矩与阻尼矩之间的竞争,局域磁矩在一个进动周期内进动角会发生小的波动.这导致图1(b)中〈mz〉的振荡曲线并不满足严格的正弦或余弦函数变化关系.因此,在应用傅里叶变换得到的频谱图中出现了频率为基频值(主频值)整数倍的高阶谐波频率.I=1 mA情形下,由于频谱中主频峰对应的幅度值较小,具有更小幅度的谐波频率没有被观测到.进一步的模拟结果显示:尽管随着电流的增强,〈mz〉振荡幅度在减小,三个电流下自由层磁矩的振荡模式却均为相同的非一致进动模式:沿长轴方向,样品中间区域磁矩的进动角度大于两端区域内磁矩的进动角(图1(c)插图).
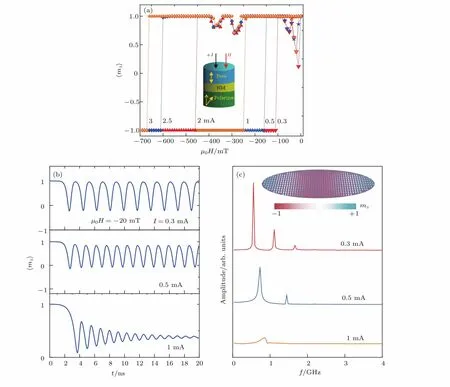
图1 不同电流下的磁翻转曲线、振荡曲线和相应的频谱 (a)自由层平均磁矩垂直分量〈mz〉随电流及磁场的演化曲线;(b)和(c)各自展示了−20 mT下不同电流对应的〈mz〉振荡曲线与频谱;(c)中的插图展示了周期性振荡中典型的磁结构暂态截图Fig.1.Magnetization switching curves,the oscillation curves and the corresponding frequency with different current:(a)Average perpendicular magnetization 〈mz〉of the free layer as a function of the applied magnetic field with different current;(b)and(c)respectively shows the typical periodic oscillation curves of〈mz〉and the corresponding frequency spectrum at fixed magnetic field−20 mT with various current;the inset in(c)shows the typical transient magnetization con figurations.
微磁模拟研究表明,样品自由层厚度对凹槽的出现位置有一定的影响.模拟中自由层磁矩具有垂直磁各向异性,极化层的极化取向偏离 +z轴方向倾斜3°.施加的电流固定为2 mA,对应电流密度为2.5×107A/cm2,外加磁场从0变化到−500 mT.自由层面内尺寸为50 nm×200 nm,厚度从1.6 nm变化到8.0 nm.基于MuMAX3[29]的模拟研究中,Slonczewski面内自旋转矩项因子为式中p为自旋极化率.对于固定的电流密度J,自旋转矩作用随着样品厚度l的增加而减小.对于自由层厚度较大的样品,相对较小的外加磁场即可驱动磁矩偏离+z轴方向.这致使〈mz〉振荡曲线中的凹槽随厚度增加而向低磁场区域移动,见图2(a).然而,在厚度l=8.0 nm的振荡曲线中,我们没有观察到凹槽的出现,这表明自旋转矩作用对于凹槽的出现是一个必不可少的条件,但不是惟一的影响因素.
图2(b)给出了厚度l=1.6 nm,µ0H=−270 mT参数下对应的〈mz〉振荡曲线,相应的频谱如图2(c)所示.频谱中的主频f1=2.78 GHz对应振荡曲线中的周期性振荡频率.而其他峰值对应的高阶频率与主频之间满足fn=n·f1,式中n为从1开始的整数.为了解磁矩的振荡模式,微磁模拟结果给出了图2(b)一个振荡周期内自由层磁矩的暂态结构,见图2(d).在这种磁模式中,磁矩的面内分量关于椭圆样品的中心或反对称分布.在磁矩的振荡过程中,两列自旋波沿着长轴方向相向传播,形成类驻波,椭圆中心处为节点位置.而沿着短轴方向,磁矩形成了一个180°的螺旋排列.

图2 不同厚度下的磁翻转曲线以及固定磁场下的振荡曲线和相应的频谱 (a)电流密度为2.5×107A/cm2时,不同自由层厚度下〈mz〉随磁场和电流的演化曲线;(b),(c)−270 mT磁场参数对应的〈mz〉振荡曲线及其频谱;(d)图(b)对应的磁振荡周期性暂态图Fig.2.Magnetization switching curves with different thickness,the oscillation curves and the corresponding frequency at a fixed magnetic field:(a)Simulated average magnetization 〈mz〉curves as a function of the magnetic field with different thickness for a given current density of 2.5×107A/cm2;(b),(c)typical periodic oscillation curves of 〈mz〉in free layer and the corresponding frequency spectrum at−270 mT;(d)snapshots of the transient magnetization con figurations for one oscillation periodic in Fig.2(b).
图3(a)展示了l=1.6 nm,µ0H=−370 mT参数下对应的〈mz〉振荡曲线,相应的频谱如图3(b)所示.可以看出高阶频率与主频f1=0.71 GHz之间仍然满足倍频的关系,fn=n·f1.微磁模拟结果显示主频对应的磁振荡模式为伴随着磁矩进动的局域磁振荡模式,如图3(b)中插图所示.在这种振荡模式中面内磁矩分量关于椭圆中心呈现出对称的分布特性.

图3 磁振荡曲线与频谱 (a)图2(a)中µ0H =−370 mT参数下对应的〈mz〉振荡曲线;(b)对应的频谱,插图为对应的磁振荡暂态图Fig.3.Magnetization oscillation curves and the corresponding frequency spectrum:(a)Oscillation curves of〈mz〉at−370 mT in Fig.2(a);(b)the corresponding frequency spectrum,the inset in(b)shows the transient magnetization con figurations.
当厚度l=3.2 nm时,〈mz〉随磁场的演化曲线中只出现了一个较为明显的凹槽.在该凹槽区域内,我们研究了−50 mT对应的〈mz〉随时间演化的振荡曲线以及频谱特性(图4(a)).尽管−50 mT对应振荡曲线与l=1.6 nm,µ0H=−370 mT参数下的振荡曲线类似(见图3(a)),两种参数下的频谱却显示出了不同的特性.如图4(b)所示,−50 mT对应频谱图中出现了一系列间谐波的频率峰:fn=f0+0.31n,其中f0=0.65 GHz为主频值.模拟结果显示,主频对应的自旋波为局域自旋波模式:磁矩的振荡被限制在椭圆的中央区域,该区域内磁矩进动角度较大,而沿长轴方向的两端磁矩进动角度较小.

图4 磁振荡曲线与频谱 (a)图2(a)中µ0H=−50 mT参数下对应的〈mz〉振荡曲线;(b)对应的频谱,插图为典型的磁振荡暂态截图Fig.4.Magnetization oscillation curves and the corresponding frequency:(a)Oscillation curves of 〈mz〉at−50 mT in Fig.2(a),(b)the corresponding frequency spectrum,the inset in(b)shows the transient magnetization con figurations.
4 结 论
基于自由层与钉扎层均为垂直磁各向异性的自旋阀结构,我们研究了小角度倾斜的极化层模型中自由层磁矩进动翻转曲线以及磁振荡模式的动力学特性.研究结果表明:小角度倾斜的极化方向可导致自由层磁矩进动曲线中多个凹槽的出现.在一定的电流范围内,凹槽出现的位置与电流大小无关.在相同的电流下,样品的厚度将会影响凹槽出现的位置.凹槽区域内可激发多种磁振荡,包括非一致进动模式、自旋驻波模式、局域自旋波模式等.下一步,我们将就该物理现象展开相关的模拟研究,探讨多个凹槽出现的物理机制.希望所得研究结果能够加深对受限于几何形状多层膜结构中的磁结构动力学行为的物理机制的理解,进一步促进自旋转矩纳米振荡器及磁存储器件的发展.
