反对称拱塔斜拉桥风场及结构力学特性

孟令藏，毛 毳

（天津城建大学 土木工程学院，天津 300384）

异形拱桥因其构造新颖奇特，近年来越来越常见于实际工程之中[1].对于异形拱桥的研究，目前主要集中在桥梁的外形设计、整体稳定性分析、抗震动力响应、非线性分析以及施工监控等方面[2-4]，而对拱桥风场特性及拱塔在风场中的力学特性研究较少.在我国公路桥涵抗风设计规范中，也没有关于异形拱桥在抗风设计方面的相关规定.本文以山西省太原市北中环桥[5]中跨为工程背景，建立有限元模型，采用雷诺平均法，研究反对称拱塔斜拉桥风场特性及拱塔在风场中的结构力学特性，以期为此类拱桥设计提供参考.

1 工程背景

北中环桥位于山西省太原市北中环与汾河交点处，由西向东依次跨越滨河西路、汾河、滨河东路，为五跨反对称拱反对称索面拱塔斜拉桥.桥梁跨径为（65+45+90+45+65）m，桥宽 43.5 m，全长 310 m，双向8车道.斜拉塔为钢拱，拱轴线采用二次抛物线，主梁为钢箱梁，主梁与钢拱之间设有反对称斜拉索.桥上5个钢拱塔，跨中拱塔最高，78 m，边跨两侧拱高48 m，次边跨拱高63 m.北中环桥立面如图1所示.

2 风场的数值模拟

2.1 模型与模拟方法

北中环桥中跨在河流中间位置，对风荷载比较敏感，因此，本文取中跨（90 m）作为节段模型，采用定常雷诺平均方法（reynolds average navier-stokes，简称RANS）[7]对节段模型风场进行模拟.

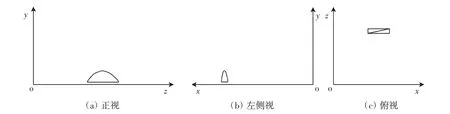
图2 流场计算域三视图

2.2 流场计算域的建立与参数设置

2.2.1 计算域的选取

根据流体计算模拟理论，流场计算域的尺寸选取应满足阻塞率小于3%[8]的要求.阻塞率的计算公式为

式中：Ab为建筑物最大迎风面积；Ad为流域横截面面积.

参照桥梁节段模型尺寸和阻塞率要求，流场计算域取890 m×840 m×1 683.5 m.其中，流场入口到结构正面距离为680 m，出口到结构背面距离为960 m，两侧到结构侧面距离为400 m，计算域上边界到拱顶距离为750 m，底边界到桥面底部距离为20 m.结构在计算域内摆放位置如图2所示.对模型及流场计算域进行网格划分，得到约500万个单元.

2.2.2 流场的边界条件与求解控制参数

表1为流场的边界条件设置，其中vz为入口处不同高度处的平均速度.

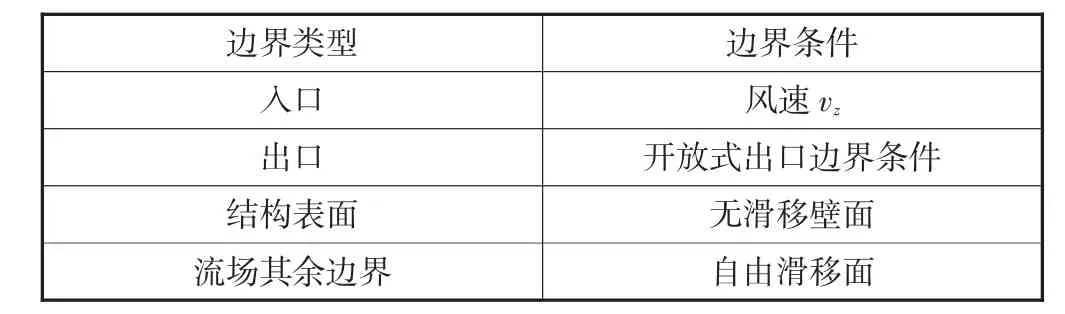
表1 流场边界条件参数设置

vz速度方向平行于x轴，大小按照指数率[9]风速剖面进行计算

式中：zb为标准参考高度，m；z为离水面高度，m；α为地面粗糙度指数，在大气边界层内可认为是常数，本工程所处地理环境属于A类地面粗糙度，故取0.12；vb为标准参考高度处的平均风速，m/s，取太原百年一遇风压，其中w0=0.45 kN/m2.

因为拱塔是曲体拱，标准模型k-ε对带有弯曲壁面的复杂湍流运动不适用.针对这一问题，重整化的RNG k-ε模型相对更为合适.RNG k-ε模型求解控制参数[10-11]见表2.

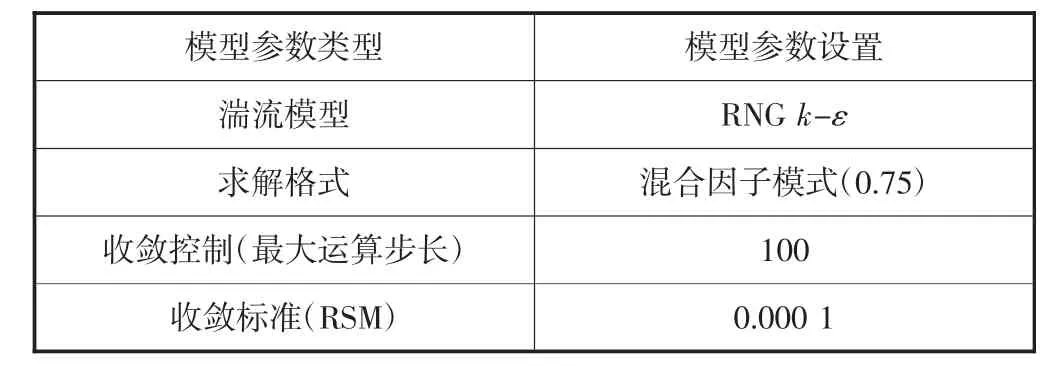
表2 求解控制参数

2.3 风场特性分析

2.3.1 拱塔风场特性分布

工程中，反对称拱塔截面呈六边形，拱顶处横截面风场速度矢量图和压强分布云图如图3-4所示.

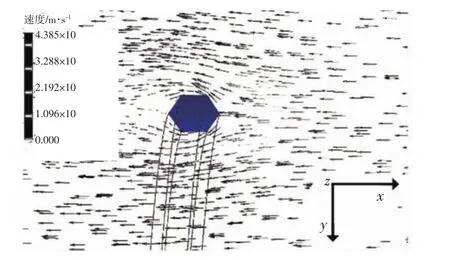
图3 拱顶截面风场速度矢量图

图4 拱顶截面风场压强分布云图

由图3可知，在迎风面气流沿拱塔上下边界发生分离，绕过两侧，在尾部附近出现边界层分离，在拱塔背风面形成少量回流，无旋涡出现.由图4可知，正压区出现在迎风面，风压自风入口方向逐渐增大，最大正压值出现在尖角，以尖角为中心向两侧对称减小；拱塔上下边界及背风面出现负压，背风面负压对称分布，向风出口方向逐渐减小.

2.3.2 主梁风场特性分布

扁平箱梁跨中横截面处流速分布如图5所示，相应的压强分布云图如图6所示.

图5 梁跨中横截面流速分布

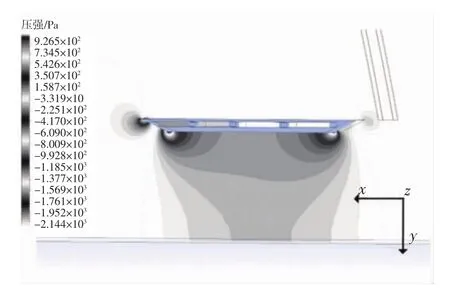
图6 梁跨中横截面压强分布云图

由图5可知，梁横截面长宽比大，迎风面处气流沿桥面上下边界发生分离，分别在上下边界层内形成速度梯度，紧贴结构壁面处流速为零，并由近边界向远离边界逐渐增大，直到达到来流速度大小；背风侧有少许回流，但无旋涡脱落.由图6可知，主梁迎风面受正压，最大压强为920 Pa，风压梯度较大；背风面受负压，最大压强为-902 Pa；梁上边界受正压，压强梯度较小；梁下边界受负压，两钝角处压强呈对称分布，压强梯度较大.

2.4 拱塔截面形状对风场特性的影响

对拱塔建立局部坐标系，得到结构模型见图7.

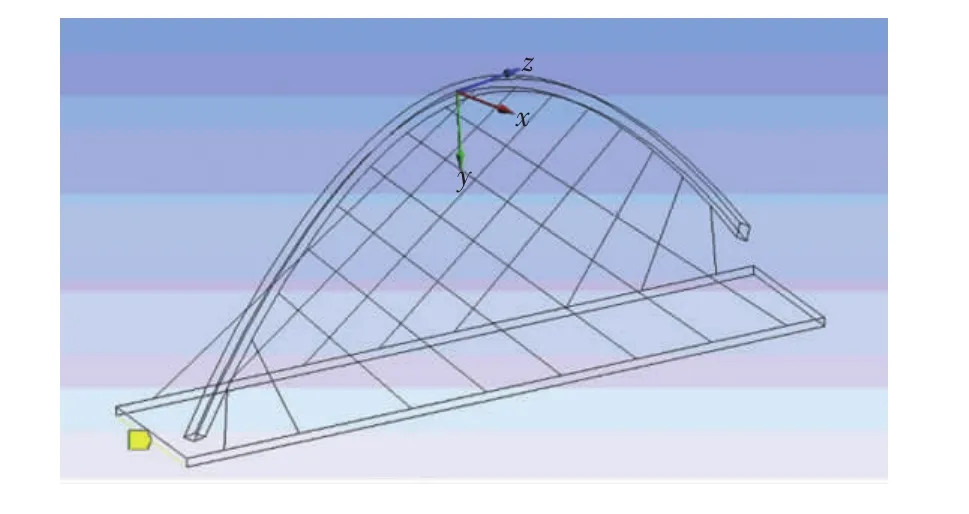
图7 结构模型

由于拱塔对风载非常敏感，在保证用钢量不变的情况下，分别取正方形、圆形作为拱塔截面形式进行流场模拟，并与原六边形截面进行对比分析.正方形、圆形及六边形截面拱顶处压强分布云图如图8-10所示.提取x轴线正向各点处压强值，分析不同截面形状压强梯度变化，如图11所示.

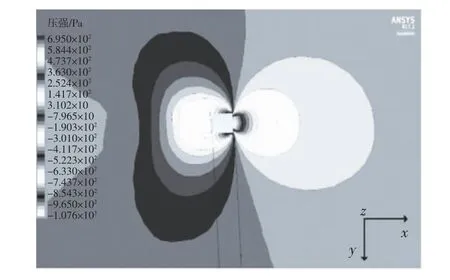
图8 正方形拱顶截面风场压强云图

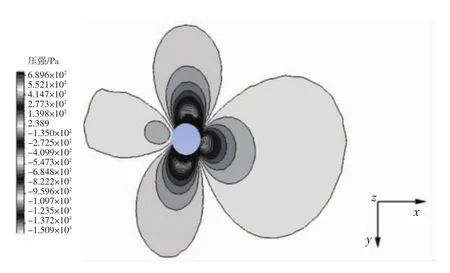
图9 圆形拱顶截面风场压强云图

图10 六边形拱顶截面风场压强云图

图11 不同截面形状拱塔沿x轴风场压强曲线

由图8-11可以看出：不同拱塔截面形状周围的风场压强分布不同；圆形截面由于流线型布置，对气流分离作用小，风场压强值最小，扰动最小；六边形拱塔压强比圆形拱塔的大，由于前缘尖角对气流的分离作用，使得其拱塔压强比正方形情况略小；正方形截面迎风面气流分离作用最强，压强最大，扰动最大.

3 结构风载力学特性模拟

3.1 结构模型及材料参数

（1）单元类型选择.反对称拱塔斜拉桥拱塔及主梁采用solid185实体单元，拉索采用link180受拉线单元模拟.

（2）材料简化及参数.由于实体拱塔结构两端分别自拱脚向拱顶2 m内灌注混凝土，所以对该混合区按等效刚度原则计算弹性模量，按等质量原则计算密度，拱塔其余部分取钢材弹性模量和密度.桥面取钢材弹性模量和密度.

（3）约束情况.根据实际工程约束情况，梁两端采用简支约束，拱塔两端设为全约束.

（4）荷载布置情况.由于对风场进行稳态模拟，故将风稳定后的压强传递到结构上进行静力分析.

（5）不考虑材料的非线性，将结构视为均质弹性体.

拱塔及主梁材料参数如表3所示.其中，钢材采用Q345qD，混凝土等级为C40.

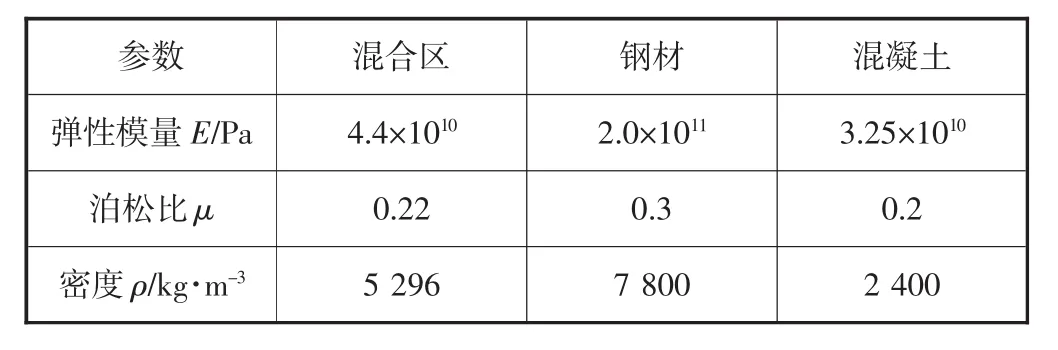
表3 材料参数

3.2 拱塔在风场中的力学特性

图12给出了拱塔在风场中的变形矢量图.

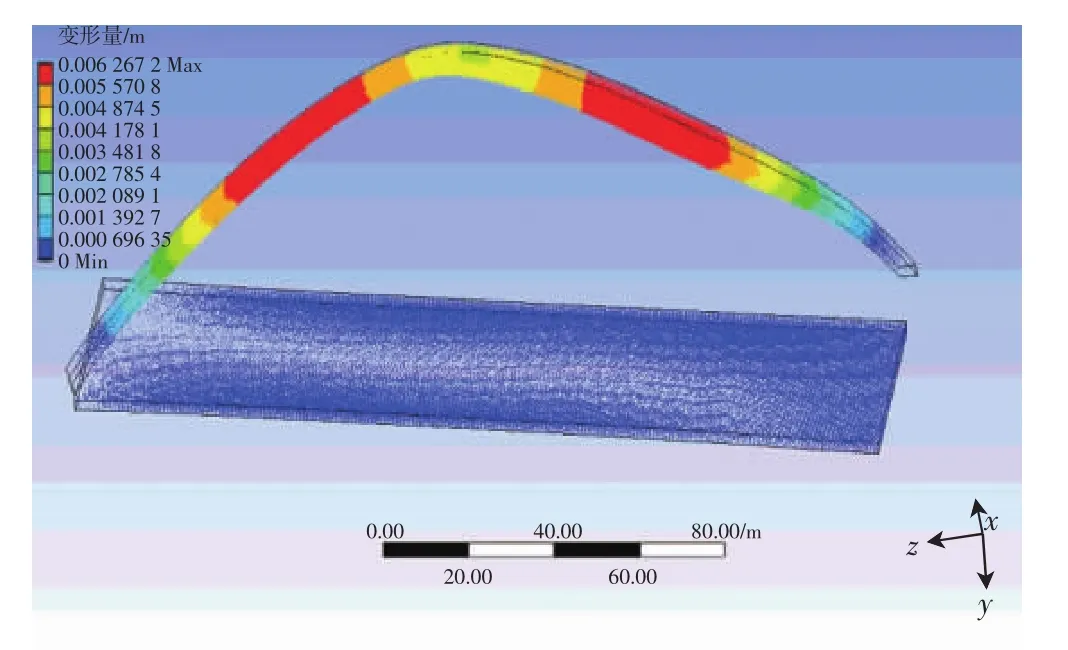
图12 拱塔风场总变形矢量图

由图12可以看出：风载作用下，拱塔发生较大变形，拱顶两侧变形较大.选取拱塔轴线若干点，提取各点处沿各轴向变形量和总变形量进行对比，见图13.

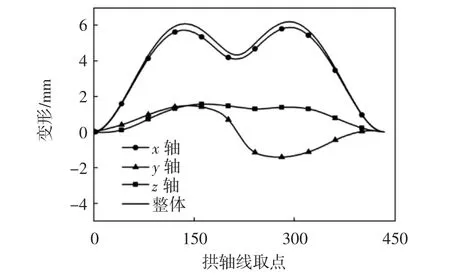
图13 拱塔轴线各提取点的变形量曲线

由图13中x轴向变形曲线可以看出：从一侧拱脚向拱顶沿拱轴线方向，变形先增大后减小，从拱顶向另一侧拱脚沿拱轴线方向，变形先增大后减小；在拱顶两侧3/5拱高处，出现拱轴线上最大变形；拱轴线的总变形量与沿x轴向变形量变化规律相似，由此可知，拱塔总变形变化由x轴向变形量决定；同时y轴向变形小于x轴向变形，拱塔两侧变形方向相反，一半拱塔竖直向上，一半拱塔竖直向下，轴线上最大变形位置不变，在拱顶两侧3/5拱高处；而z轴向变形量最小，分布规律相同，最大变形位置不变.由于拱塔受到拉索的空间拉力作用，拉索的分布不对称性引起反对称拱塔最大变形位置的特殊性，有别于一般拱桥拱顶所出现的最大变形.

4 结论

（1）在拱塔周围一定范围内风场压强受扰动较明显，不同截面形状正压区和负压区分布形状不同和大小范围不同；正方形截面压强最大，六边形截面压强次之，圆形截面压强最小.对于风载作用下的反对称拱塔斜拉桥，为了减小结构对风场的扰动，并考虑到风向角度的影响，选择圆形拱塔截面较为理想.

（2）扁平主箱梁背风面出现边界层分离，有少量回流，尾流区未出现旋涡.扁平主梁对原有流场状态扰动范围相对较小，尾流区无旋涡出现，降低了风场因自身受到扰动所引起的对结构的反作用.在考虑风场因素影响的情况下，反对称拱塔斜拉桥宜选择扁平主梁形式.

（3）反对称拱塔斜拉桥在风载作用下，斜拉索的不对称分布使得拱塔轴线上最大变形不在拱顶处，而是在3/5拱高处，两侧各有最大变形点，且关于拱顶对称分布.一般拱桥拱塔轴线最大变形多出现在拱顶处，而由于反对称拱塔斜拉桥拱塔变形不同于一般拱桥，因此对其特殊的变形位置应采取有针对性的抗风措施.