全等三角形常见错题剖析
2018-09-21蔡大双
蔡大双
一、忽略“对应”
1.文字表述与数学语言有区别.
【例1】如图1,在 ABC中,∠C=90°,AC=10,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问AP=_______时,才能使△ABC和△APQ全等.

图1
【错解】∵△ABC与△APQ全等,
∴BC=PA(全等三角形性质),
∴PA=6.
【错因剖析】这种错误在于忽略了两个三角形全等时“对应的多样性”.在△ABC和△APQ中,直角边PA既可以与BC是对应边,也可以与CA是对应边,因此答案不唯一.
【订正】第一种情况:BC与PA是对应边,答案是BC=PA=6;
第二种情况:PA与CA是对应边,答案是PA=CA=10.
注:如果题目问的是AP=______时,△ABC≌△QPA,则答案唯一,此时两三角形的对应边已经确定,AP=CB=6.
2.运用“AAS”时,S不“对应”.
【例2】如图2,在△DBC 中,∠DBC=90°,在△AEC中,∠ACE=90°,AE垂直DC交DC于点F,且AC=BC,请说明AE=CD.
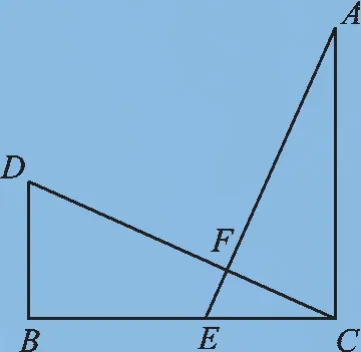
图2
【错解】在△DBC中,∠D+∠DCB=90°,
在Rt△AEC中,∠ACE=90°=∠ACD+∠DCB,
∴∠D=∠ACD(等式的基本性质).
在△DBC与△CFA中,

在Rt△ACE中,直角边AC<斜边AE,所以AE≠CD.
【错因剖析】上述过程错误的原因是,在用“AAS”证明全等时,选择的边AC是∠AFC的对边,边BC是∠D的对边,因此对应关系出现了问题,所以证明出的结果是错误的.

二、错用等式基本性质
【例3】如图,∠1=∠2,∠A=∠B,证明:AE=BE.
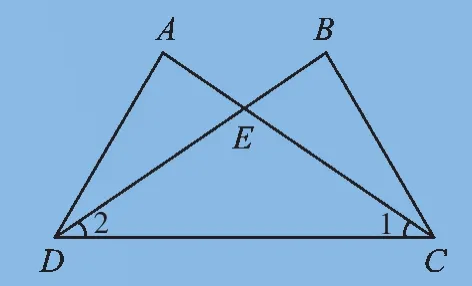
图3

【错因剖析】这种错误主要是在证明两个三角形全等过程中错用了等式的基本性质一:等式两边同加(同减)同一个数(式子),等式仍然成立.将两个全等三角形同时减去相同的部分,并不能说明剩余部分的三角形全等,只能说明它们面积相等.
【订正】在△ADC与△BCD中,

