火眼金睛识全等
2018-09-21江苏省苏州外国语学校八韦昊宇
江苏省苏州外国语学校八(3)班 韦昊宇
本学期第一章是有关全等三角形的知识,很多同学明明对概念了然于胸,自己做时却不知从何下手,这就需要我们用一双火眼金睛来找出题目中的全等三角形了.
我们先来回顾一下全等三角形的五种判定方法:SSS(边边边)、SAS(边角边)、ASA(角边角)、AAS(角角边)、HL(一条斜边与一条直角边).
一、根据结论找出全等关系
【例1】已知图1中AD⊥CE于D,BE⊥CE于E,AC=BC,∠ACB=90°,求证:DE+EB=AD.

图1
【分析】由结论DE+EB=AD以及图中CD+DE=CE,可知道需要证明 AD=CE,CD=BE.如此,我们不难发现,只要证明△ACD与△CBE全等即可.
∵AD⊥CE,BE⊥CE,∴∠ADC=∠CEB=90°,∴∠DAC+∠ACD=90°.
又 ∵∠ACB=90°,∴∠ACD+∠BCE=90°,∴∠DAC=∠BCE.又 ∵CA=CB,∴△ACD≌△CBE(AAS).
二、巧添辅助线构造全等
【例2】如图 2,D为 BC中点,AC平分∠DAE,2AD=CE,求证:AB=CE.
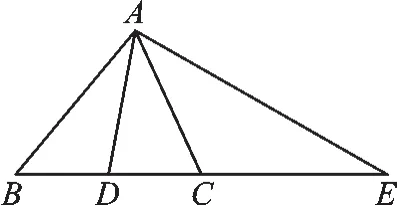
图2
【解法】要解此题,我们需先倍长中线,如图3,延长AD使DF=AD.通过已知条件证明△ABD与△FCD全等,再证明△ACF与△ACE全等,之后便可得到AB=CE.

图3
教师点评:生活中不缺乏美,而是缺乏发现美的眼睛;几何证明中不缺乏乐趣,而是缺乏发现乐趣的角度.全等的三角形有时会直接存在于图形中,需要同学们像孙悟空一样用自己的“火眼金睛”透过现象看本质;有时候却令人烦恼,图形中根本没有可以用的全等图形,这时候就需要同学们静下心来,仔细观察图形,结合已知条件,添加适当的辅助线来构造全等的图形.朱老师套用《游击队之歌》的歌词,改编为“没有边,没有角,自有图形中的隐含条件现出来;没有全等,没有相互关系,咱们添加辅助线自己造”,方便同学们记忆.
