从变换的角度看全等
2018-09-21周青松
初中生世界 2018年34期
周青松

几何是初中数学学习的重要内容,八年级数学最初几章就是几何知识.学好了几何,有利于同学们思维的发展、思路的拓展及解题能力的提高.“全等三角形”的学习是建立在“平面图形认识”的基础上的,同学们有了一定的几何基础,可从变换的角度再次认识“全等三角形”.
一、平移
我们通过平移的方式使得两个三角形重合可以验证三角形全等,即两个三角形满足三条边对应相等,三个角也对应相等.
1.直接平移.
如图1,直接平移使得△ABC与△DEF重合即可.即△ABC≌△DEF,从而得到对应元素相等.

图1
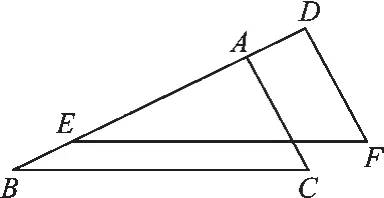
图2
2.共线平移.
如图2,△ABC与△DEF沿着ED边平移至重合.即△ABC≌△DEF,从而得到对应元素相等.
二、旋转
我们通过旋转的方式可以验证三角形全等,两个三角形有公共顶点.
1.旋转180°.
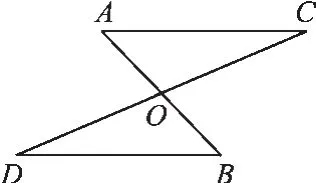
图3
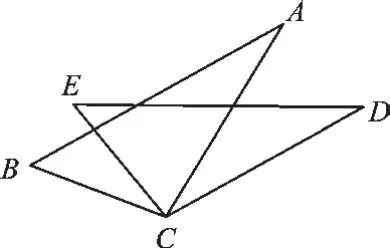
图4
如图3,△AOC绕O点旋转180°得△BOD.易证得△AOC≌△BOD,从而得到对应元素相等.
2.旋转任意角度.
如图4,△ACB绕C点旋转任意角度得△DCE.即△ACB≌△DCE,从而得到对应元素相等.
三、翻折
我们通过翻折的方式可以验证三角形全等,两个三角形有公共边.
如图5,△ABC与△ABD有公共边AB,沿AB翻折重合即可.即△ABC≌△ABD,从而得到对应元素相等.
四、总结
通过平移、旋转、翻折三种方式验证了三角形全等,也帮助我们顺利地找到了两个全等三角形中的对应元素.通过上述探究我们还可以把全等三角形按公共角和公共边进行分类.
第一类:有公共边的两个全等三角形,如图5、图6、图7.

图5
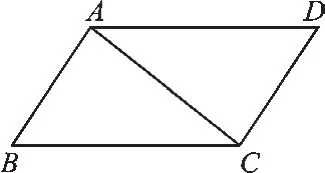
图6
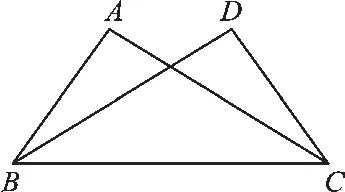
图7
第二类:有公共角的两个全等三角形,如图8、图9.

图8
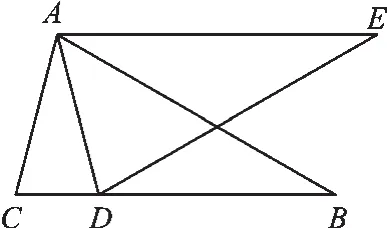
图9
