巧连辅助线 事半而功倍
2018-09-21张茜
张 茜
一些较难的证明题往往需要添加辅助线才能证明,下面为同学们梳理五种常见辅助线的作法.
一、补全图形
【例1】如图1,在△ABC中,AB=AC,∠BAC=90°,BD平分∠ABC交AC于点D,CE垂直于BD,交BD的延长线于点E.求证:BD=2CE.

图2
【分析】要证明BD=2CE,就要找到与2CE相等的线段.这里BD⊥CE,且BD平分∠ABC,所以想到了补全图形,构造全等.
证明:如图2,延长CE、BA交于点F,
易证Rt△BEC≌Rt△BEF(ASA),
∴CE=EF,∴CF=CE+EF=2CE.
∵∠ABD=∠FCA(同角的余角相等),
易证Rt△CAF≌Rt△BAD(ASA).
∴BD=CF.
又∵CF=2CE,∴BD=2CE.
【说明】补全图形,构造出2CE,再利用三角形全等,证得结论.
二、倍长中线法构造全等
三角形问题中涉及中线(中点)时,将三角形中线延长一倍来构造全等三角形是比较常用的解题思路.
【例2】如图3,在△ABC中,∠A=90°,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试探索线段BE、CF及EF之间的等量关系,并加以证明.

图3
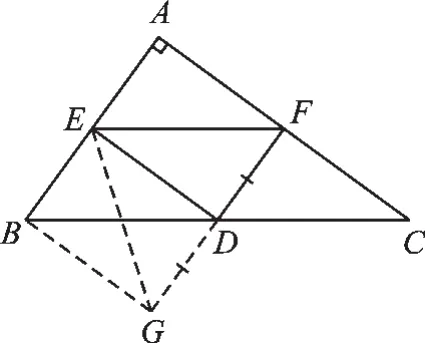
图4
【分析】此题中需要倍长FD,连接BG,达到了将△DFC绕点D旋转180°的效果.再加上DE⊥DF,三线合一,故连接EG形成等腰△EGF.再证出△FDC≌△GDB后,将边CF及∠C转移到△EBG中,且易证∠EBG=90°,则可得证.
证明:如图4,延长FD至点G,使得FD=DG,连接BG,EG.易证△FDC≌△GDB.
∵DE⊥DF,DF=DG,∴EG=EF.
易证∠EBG=90°,
∴BE2+BG2=EG2,即 BE2+CF2=EF2.
【说明】倍长中线法的解题思路,就是见到中点,将与中点连接的线段倍长,目的是通过几何变换将分散的条件集中起来,所以说见到图形某边上的中点是我们利用倍长中线法的一个重要信号.
三、利用角平分线构造全等
角平分线所在的直线是角的对称轴,在证明全等过程中不仅提供了两个相等的角,还有一条公共边.利用角平分线在角的两边截取相等的线段,或向两边作垂线,进而构造出全等三角形是常用的证明方法.
【例3】已知,如图5,AC平分∠BAD,CD=CB,AB>AD.求证:∠B+∠ADC=180°.

图5

图6
【分析】因为AC是∠BAD的平分线,所以容易想到过点C向∠BAD的两边作垂线,构造直角三角形,通过证明三角形全等解决问题.本题考查了角平分线性质的应用.
证明:如图6,作CF⊥AB于F,CE⊥AD交AD延长线于E,易证Rt△CDE≌Rt△CBF(HL).
∴∠B=∠CDE.
∵∠ADC+∠CDE=180°,
∴∠B+∠ADC=180°.
【说明】关于角平分线的问题,常见图7、图8的两种辅助线.用好角平分线模型,根据轴对称性构造全等三角形是常见的一种题型,须熟练掌握.
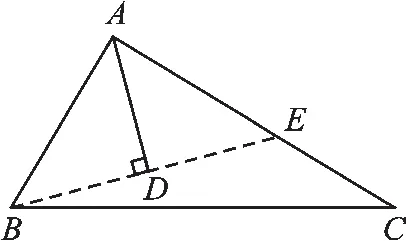
图7

图8
四、作平行线
在三角形问题中遇到有相等的角或等腰等条件时,可通过作平行线,将相等的角转换到某一个三角形中,得到另外的等腰三角形或相等的角,从而为证明全等提供条件.
【例4】如图9,在等腰△ABC中,AB=AC,在AB上截取BD,在AC的延长线上截取CE,且使CE=BD,连接DE交BC于F.求证:DF=EF.
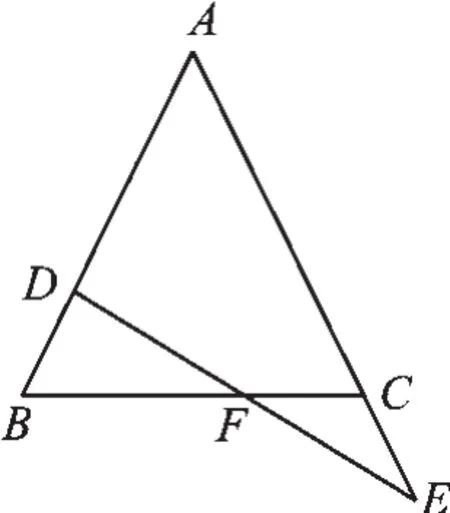
图9
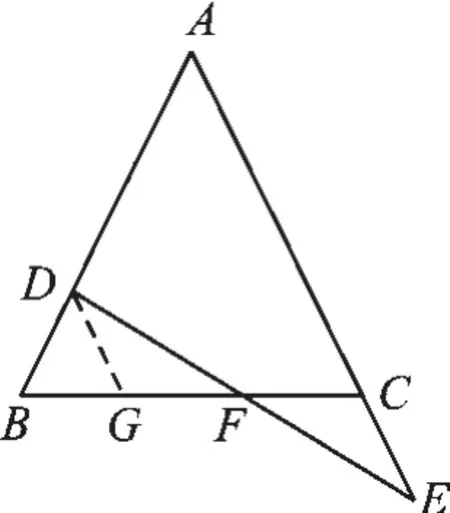
图10
【分析】要证DF=EF,需要借助三角形全等,可以将CE平移至DG处,这样的平移不仅构造了全等三角形,而且形成了等腰△DBG.再证明△DGF≌△ECF即可.
证明:如图10,过点D作DG//AC,交BC于点G.
∵AB=AC,DG//AC.
易证BD=DG,∴DG=CE.
又∵DG//AC,
∴∠GDE=∠CEF,∠DGF=∠FCE.
∴△DGF≌△ECF,∴DF=EF.
【说明】将分散的条件集中,可以采用“平移”变换的方法构造全等三角形.
五、截长补短法
一般地,当已知或所证结论中涉及线段的和、差及倍数关系,且这两条线段不在同一条直线上时,通常可以考虑用截长补短法,在长线段上截取一部分使之与短线段相等,或将短线段延长使其与长线段相等,再利用三角形全等的有关性质加以说明.
【例5】如图11,AD∥BC,点E在线段AB上,∠ADE=∠CDE,∠DCE=∠ECB.求证:CD=AD+BC.

图11

图12
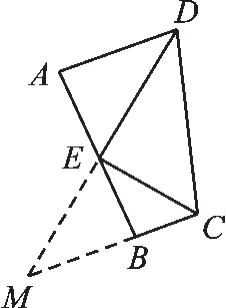
图13
【分析】要求证CD=AD+BC,可考虑“截长”,在CD上截取CF=CB,再证DF=DA,这就转化为证明两线段相等的问题了.
证明:(截长法)如图12,在CD上截取CF=CB,∴△FCE≌△BCE(SAS),∴∠2=∠1.
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠DCE+∠CDE=90°.
∴∠2+∠3=90°,∠1+∠4=90°.
∴∠3=∠4.
∴△FDE≌△ADE(ASA),∴DF=DA.
∵CD=DF+CF,∴CD=AD+BC.
证明:(补短法)如图13,延长DE交CB的延长线于点M.
∵AD∥BC,∴∠ADE=∠M.
∵∠ADE=∠CDE,∴∠CDE=∠M,∴CD=CM.
∵∠DCE=∠ECB,∴DE=EM,∴△ADE≌△BME(ASA).
∴AD=BM,即CD=CM=AD+BC.
【分析】本题考查全等三角形常见辅助线的做法,截长法或补短法.
以上是全等三角形中,五种常见的辅助线作法.同学们,你们掌握了吗?形成自己的解题习惯,拥有良好的解题基本功,不仅要掌握知识结构,培养思维能力,还要积累解题经验,才能在面对问题时迎刃而解.
