运输取送系统模型设计
2018-09-21陈时陈宪议
陈时,陈宪议
运输取送系统模型设计
陈时,陈宪议
(四川中康大件运输有限责任公司,四川 成都 610036)
基于车辆取送货系统问题特点,联系企业的实际情况对单源、多车辆带有软时间窗约束的路径优化问题进行了深入研究。依照简化实际问题研究思路,对企业面临的取送线路优化问题做出了有选择性到达的单源多路径的软时间约束路径优化模型。
物流公司;送货业务;取送货系统;利润率
1 问题描述与分析
D公司是一家专业的第三方物流公司,每日都会有从中心点到各下属节点的运输送货业务,相应的各节点也有关于中心节点的货物运输业务。
企业现有的运输取送方式主要遵循“分区取送”“就近选择”“满载即归”的规则。具体的做法是将下属节点按照地理位置划分为几大区域,每个区域有不同的车队负责取送服务,每次车辆出发都由节点的取送质量计算好需要服务的节点,每到一个节点后选择距当前位置最近的节点作为下一站服务的对象。如果运输过程中车辆满载或即将满载,则车辆立即返回节点,余下工作交由加班车辆完成。本模型中暂不考虑加班车辆。根据取送货系统的定义可知,系统需要选择最优的路径,使车辆的利润率最高,且需要考虑考超载和到达时间对客户满意度的影响[1-2]。
运输取送问题的优化目标主要包括3个部分:①最大化整个系统过程的总收入,收入则与货物种类、货物移动距离有关;②最小化系统操作过程的运输成本由运输距离决定;③最小化系统运作过程中产生的时间成本包括等待成本和晚到成本,基于此可提升服务质量和客服满意度。
由3个部分组合为最终的优化函数,即达到利润的最优值。在整个系统中,为了使收入达到最高,应选择更多的节点运输,但这样会使得运输路径的距离变长,运输成本增加,运输时效降低,而且还有可能造成车辆超载等实际问题。所以,如何在准载范围内平衡三者的数量关系就是本文要达到的目的。
运输取送问题可以理解为:在只有1个运输中心的情况下,有∈(1,2,3,…)辆车,每辆车的额定载货量为k,行驶速度为k,并在运输过程中,不允许有超载的情况。有(=1,2,3,4,…)个运输节点提出了业务需求。其中,各节点的业务作业方式包括单一取货模式、单一送货模式、取送结合模式。第个节点需求的质量为i[,],其中,为取货质量,为送货质量。第个节点的时间限制为i[,],为最早时间,为最晚时间。,分别为早到时的等待成本和晚到的惩罚成本,都属于常数。从中心点出发,最后返回中心点。过程中至少行驶1个节点,每个节点也只能由一辆车作业。需要在充分考虑系统收入、车辆行驶总费用、车辆违背时间窗造成的损失的情况下,规划好所有车辆的运输路线,使得整个系统的利润取得最大值。
2 运输取送系统模型的设计
2.1 设定条件
本文的运输取送货系统是对实际业务的一种理想化模型。由于能力有限,且为了简化模型结构,模型有以下假设条件和已知变量:①所有的客户服务优先等级相同;②在单个节点的取送操作中,只能由一批次车辆作业操作;③车辆数、节点数、节点货物质量,取送性质已知;④各车辆的最大载重量已知,并规定严禁超载;⑤各节点的标准作业时间范围已知,超出时间约束范围以外的需要付出成本,惩罚系数已知;⑥系统取送过程中,为了求利润最大值可选择性地到达某节点;⑦节点坐标,车辆速度已知且不变;⑧车辆在取送操作间隙的装卸时间不予考虑;⑨成本只与距离相关,收入则受距离、质量的影响;⑩系统只考虑节点与中心点的互动,不考虑节点之间的作业情况。
2.2 变量描述
对模型中涉及的变量进行以下界定,包括定义、取值方式、范围等。其中,包括2个决策变量和多个已知常量:①对所有节点按顺序升序编号,中心起点标号为0,其中=(0,1,2,3,…,)。②为车辆编号,=(1,2,3,…)。③k为车辆的行驶速度,其中∈(1,2,3,…),k∈^+。④ij为节点到节点的距离,由节点坐标求得,其中=(0,1,2,3,4,5…),=(0,1,2,3,4,5…)。⑤,分别为早到时的等待成本和晚到的惩罚成本,都属于常数。⑥i,i分别为节点的时间窗最早时间(作业最早时间)、最晚时间(作业最晚时间)。⑦ik为车辆到达节点时间,其中=(1,2,3,…),=(0,1,2,3,4,…)。⑧k为车队的最大载重量,其中=(1,2,3,…)。⑨为收入系数,为路费成本系数。⑩i为节点的送货质量,i为节点的取货质量。其中,=(0,1,2,3,4,5,…)。当i=0,表示节点只有取货作业;同理,当2i=0,表示节点只有取货作业。⑪ik为当前车辆的载重量。其中=(1,2,3,…),=(0,1,2,3,4,…)。⑫为所有车辆行驶的总距离。⑬ik为当前节点时车辆的载重量。其中=(1,2,3,…),=(0,1,2,3,4,…)。
定义2个决策变量如下。

2.3 建立运输取送货模型
其中先引入以下函数。
收入函数()为整个系统运输货物的运输总输入收入,主要包括送货收入和取货收入两部分。
取货收入:
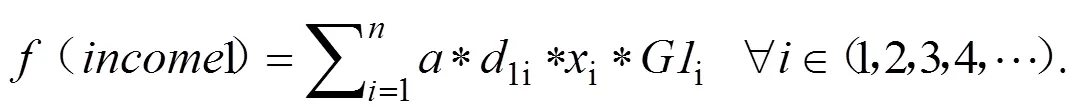
送货收入:
()为运输系统的运输成本,计算公式为:
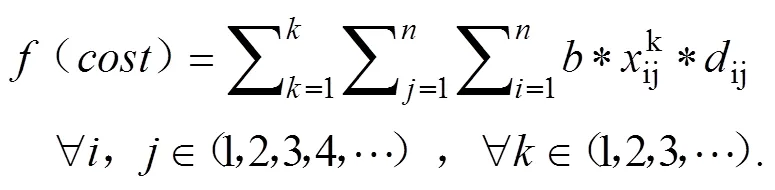
()为到达时间,计算公式为:
对于惩罚函数,由于节点作业时间的限制,论文有软时间窗限制。在时间窗以外,有一定的惩罚成本,其中,惩罚系数已知并不变。
早到等待成本函数为:
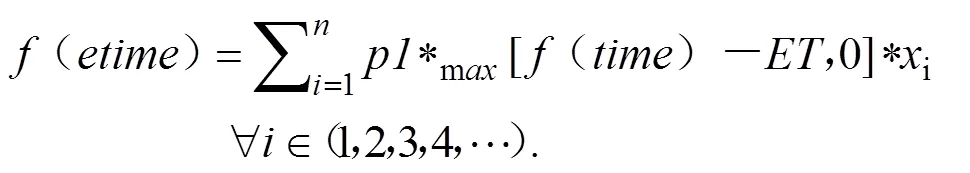
迟到惩罚成本函数为:
综上所述,得到的最终优化模型为:
=(i)-()-()-().(1)
St:

i≤ik≤i
(3)


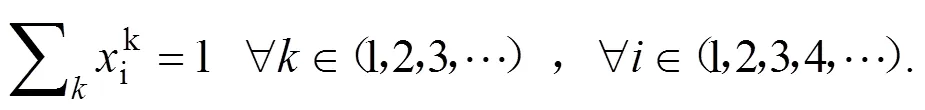
式(1)为该模型的目标函数,优化目的为利润最大值,其中,包括收入函数、运输成本函数、时间成本函数;式(2)说明辆车不能超过各自的额定承载重量;式(3)为车辆到达节点的时间需要在最早作业时间和最晚作业时间之间;式(4)为每辆车必须经过至少一个节点(除中心点外);式(5)为车辆需要从中心点出发;式(6)约束了每个节点只可以由唯一的车作业。
[1]周康.求解TSP算法[J].计算机工程与应用,2007(29).
[2]高海昌,冯博琴,朱利.智能优化算法求解TSP问题[J].控制与决策,2006(03).
[3]谷浩.带时间窗的车辆路径问题的研究与应用[D].哈尔滨:哈尔滨工业大学,2014.
[4]张晨光.统计模型在物流规划中的应用[J].技术与方法,2016(10).
[5]张燕翠.无线传感器网络中继器放置问题算法研究[D].杭州:杭州电子科技大学,2011.
2095-6835(2018)18-0128-02
F224.7
A
10.15913/j.cnki.kjycx.2018.18.128
〔编辑:张思楠〕
