基于Logistic混沌映射的数字图像加密算法*
2018-09-21郑继明汤智睿邓建秀林姚
郑继明,汤智睿,邓建秀,林姚
基于Logistic混沌映射的数字图像加密算法*
郑继明,汤智睿,邓建秀,林姚
(重庆邮电大学理学院,重庆 400065)
针对图像信息传输的安全问题,运用混沌映射加密理论,提出了一种新的数字图像加密算法。该算法运用Logistic-control-Logistic(LCL)混沌映射生成混沌序列,并结合SCAN模式对图像进行置乱,再对图像进行多方向扩散。实验与加密性能分析表明,该算法具有很好的安全性,且执行效率高,容易实现。
图像加密;LCL混沌映射;SCAN模式;多方向扩散
使用互联网传输数字图像具有方便快捷、开支小等优点,但美中不足的是,数字图像在网络上传输存在许多安全隐患。如何保证数字图像的安全传输是备受人们关注的问题。由于图像数据量大、强冗余性、相邻像素间的强相关性以及现在图像攻击技术的快速发展,传统的图像加密算法已不能满足实际需要。
混沌系统具有不确定性、不可预测、非周期和初值敏感性,这正是密码学中密钥和密钥流寻求的特性。许多学者开展了基于混沌理论加密的研究,得到了一些有效的加密方法。文献[1-3]中提出,将SCAN模式用于图像加密,且在加密过程中使用具有扩散性的随机序列;利用Logistic混沌序列的随机性、对初始条件敏感和迭代不重复的特性,得到了一些基于Logistic映射的数字图像加密算法[4-5];Hua[6]通过对混沌映射的参数进行动态控制,使原混沌系统具有更复杂的混沌行为;文献[7]用高维混沌系统对图像加密,Akram[7]将SPN与混沌理论融合,设计出新的算法用于图像加密;文献[8]将2个一维混沌映射融合为二维的混沌映射对图像进行了加密;Wang[9]使用混沌映射对彩色图像加密;Liu[10]通过变化参数改进 Baker映射,增强了初值的敏感性,通过动态参数的映射加密图像,使算法能够有效抵抗相空间重构攻击。Logistic混沌映射表达式简单且性能优良,非常适合数字图像加密。但是,该映射存在不动点、稳定窗等不足,产生的混沌序列不能保证图像加密足够安全。本文基于LCL映射、SCAN模式提出了一种新的图像加密算法,该方法具有较大密钥空间。仿真结果表明,该算法能有效抵抗差分攻击、暴力攻击等,具有较高的安全性。
1 Logistic与Logistic-control-Logistic映射的混沌特性
经典的Logistic映射是一个一维离散时间非线性映射,其表达式为:
n+1=4n(1-n). (1)
式(1)中:∈[0,1]为映射的参数;n∈[0,1]。
当∈[0.9,1]时,Logistic映射具有混沌特性。
LCL映射是基于Logistic映射的组合映射,它使用一个Logistic映射动态控制另一个Logistic映射的参数。图1(a)给出了LCL的结构,其中,1()、2()均为Logistic映射,()为变换函数。1()生成序列控制2()的参数,称为控制映射;2()为最终产生混沌序列的映射,称为种子映射;变换函数()将1()的输出映射到2()参数的混沌范围,使得种子映射2()总是具有混沌行为。
LCL的数学表达式如下:
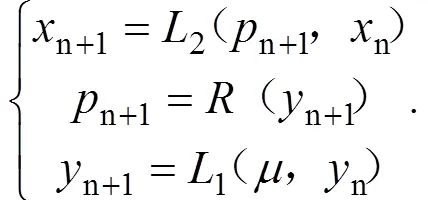
在式(2)中,1()的输出为[0,1],而2()的参数混沌范围约为[0.9,1]。变换函数()是将1()的输出映射到2()参数的混沌范围,即():[0,1]→[0.9,1]。为了简化计算,定义变换函数()为下面的线性函数,即:
n+1=1-0.1n+1. (3)
分别将式(1)、式(3)代入式(2),则可得:

任意给定初始值x0,y0以及常数μ的值,可由式(4)生成一组混沌序列{xn}。图1(b)给出了LCL映射的李雅普诺夫指数(LE)值。
2 置乱与扩散模式
2.1 SCAN模式置乱
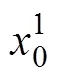
以原图中小块1,1为例,采用索引排序对序列排序,得到置换序列,从而将小块1,1表示成二维数组,选取{二次对角型,连续正交型,平行对角线型,螺旋型}扫描模式,经过2次,将得到的图像序列表示成二维数组,结果如图2所示。

图2 二维数组置乱示例
在此需要注意,由于每一次置乱都是在块内进行,因此,需要通过螺旋矩阵再对整幅数字图像进行整体置乱,使每个像素可能出现在任何位置。
2.2 多方向扩散
传统的扩散方式是1个像素点或2个像素点单方向地向下一个像素点扩散。为了获得较好的扩散效果,这种扩散方式往往周期比较长。本文设计多方向扩散机制,1个像素点从4个不同的方向朝4个像素点方向扩散,以缩减扩散周期,获得高效的加密算法,具体扩散方式如下:


3 加密算法设计
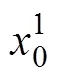

图3 算法流程图
4 实验结果及加密性能分析
利用本文提出的算法对Lena图进行实验,原始图像及其灰度直方如图4(a)、图4(c)所示,原始图像加密后效果及加密后灰度直方图如图4(b)、图4(d)所示。
4.1 密钥空间
加密图像能否抵抗穷举攻击与密钥空间的大小有关,只有足够大的密钥空间,才能抵抗穷举攻击。本算法中共有7组密钥,共21个密钥,令每个密钥的最大精度为10-14,那么,密钥空间大小为:(1014)21=10294.在相同精度下,本算法的密钥空间远大于文献[2]的密钥空间,具有更高的安全性。

图4 实验结果
4.2 密钥灵敏度分析

对其他密钥进行相应的改变时,也可以得到类似的解密结果图。从图5(a)、图5(b)、图5(c)中可以看出,当密钥中的任何一个进行10-14级的微小改动时,解密结果图与原始明文图像完全不同。这说明,本文的加密算法能够抵挡各种敏感性攻击。
4.3 相关性分析
图4(a)原始图像水平、垂直和对角方向的相关性分别如图6(a)、图6(b)、图6(c)所示,采用本算法加密后,水平、垂直和对角方向的相关性分别如图7(a)、图7(b)、图7(c)所示。

图7 加密图像相关性
从图6和图7中可以明显看出,原始图像3个方向上的像素具备较强的相关性。经过本文所示的算法加密后,像素之间基本不具备相关性。
4.4 信息熵测试
图像的信息熵可以度量灰度值的分布,结果显示,信息熵越大,其灰度分布越一致。对于理想的随机图像,其信息熵等于8.
本文加密图——图4(b)的信息熵为7.997 4,已经比较接近理想值8,即加密之后图片灰度分布较一致。
4.5 像素改变率和一致平均改变强度
像素改变率(NPCR)和一致平均改变率(UACI)用于测试整个加密图中一个像素改变的影响。本文将每个图像的第一个像素的灰度值减少5,以Lena为例计算出像素的改变率为99.630 7,一致平均改变强度为33.402 6.
表1给出了本文算法与文献[7-9]关于相关性、信息熵、像素改变率和一致平均改变率的对比结果。
表1 本文算法与文献[7-9]的结果对比
加密图像文献[7]文献[8]文献[9]原始图像 相关性分析水平0.003 3-0.004 8-0.006 60.002 00.949 2 垂直0.003 8-0.011 2-0.008 90.003 80.970 5 对角0.002 5-0.004 50.042 4-0.001 90.960 7 信息熵7.997 47.996 37.996 57.997 1 NPCR99.630 799.622 899.609 299.586 4 UACI33.402 633.704 133.632 233.253 3
5 结束语
本文给出了利用LCL映射对图像加密的算法,通过LCL混沌映射,加密算法具备了更大的密钥空间。在置乱阶段,先使用SCAN模式进行块内置乱,再用螺旋矩阵进行整体置乱;在扩散阶段,控制每个像素点直接扩散到4个像素点,有效地减小了像素点的相关性。从仿真结果与性能分析中可以看出,像素之间的相关性变得非常小,像素改变率和一致平均改变强度达到了比较理想的结果,且本算法具有较高的安全性。
[1]Maniccam S S,Bourbakis N G.Image and video encryption using SCAN patterns[J].Pattern Recognition,2004,37(4):725-737.
[2]Bourbakis N,Alexopoulos C.Picture data encryption using SCAN patterns[J].Pattern Recognition Journal,1992,25(6):567-581.
[3]Bourbakis N.Image data compression encryption using G-scan patterns[C]//IEEE Conference on SMC.Orlando: FL,1997:1117-1120.
[4]王琳娟.基于Logistic映射的多重图像加密技术[J].科学技术与工程,2011,11(8):1671-1815.
[5]黄胡晏,绕从军.一种新型混沌图像加密算法[J].华中师范大学学报,2017,51(4):441-448.
[6]Hua Zhongyun,Zhou Yicong.Dynamic Parameter-Control Chaotic System[J].IEEE Transactions on Cybernetics, 2016,46(12):3330-3341.
[7]Akram Belazi,Ahmed A Abd El-Latif,Safya Belghith.A novel image encryption scheme based on substitution-permutation network and chaos[J].Signal Processing,2016,128(11):155-170.
[8]Hua Zhongyun,Zhou Yincong,Pun Chi-Man.2D sine logistic modulation map for image encryption[J].Information Sciences,2015,297(C):80-94.
[9]Wang Xingyuan,Teng Lin,Qin Xue.A novel colour image encryption algorithm based on chaos[J].Signal Processing,2012,92(4):1101-1108.
[10]Liu Lingfeng,Miao Suoxia.An image encryption algorithm based on Baker map with varying parameter[J]. Multimedia Tools and Applications,2017,76(15):16511-16527.
郑继明(1963—),男,四川简阳人,教授,主要从事数学建模方法研究。汤智睿(1997—),男,四川广安人。邓建秀(1997—),女,四川内江人。林姚(1995—),男,四川绵阳人,信息与计算科学专业本科生。
重庆邮电大学大学生科研训练项目(编号:A2017-70)资助
2095-6835(2018)18-0008-04
TP309.7
A
10.15913/j.cnki.kjycx.2018.18.008
〔编辑:白洁〕
