车门限位器仿真与扭矩试验研究

□ 周 毅 □ 罗汉明 □ 付王梁

1.同济大学新能源汽车工程中心 上海 201804

2.同济大学汽车学院 上海 201804

1 研究背景

车门限位器是车门总成的一个关键部件，直接影响开关车门的舒适性、车门开关力的大小、车门寿命，以及噪声、振动与声振粗糙度性能等。现在国内针对车门限位器的设计指导资料较少，更多的是通过大量试验来达到要求。何睿等[1]通过作图法设计了拉带式车门限位器，黄明菲[2]、刘遗勋[3]、王延伟等[4]对拉带式车门限位器拉带的布置和轨迹进行了说明和研究。而针对限位器的形状设计，由于技术难度较大，目前仅是理论分析较多。汽车行业竞争激烈，应用计算机辅助工程技术中的多体动力学仿真技术，可以大大降低开发成本和缩短开发周期。因此，合理利用计算机辅助工程软件如Virtual.Lab Motion等来指导车门限位器的设计，是值得研究的课题。

2 车门限位器建模

多体动力学仿真软件一般将多体系统定义成四个部分的代数-微分方程，具体为部件、约束、力和自定义[5]。确定限位器各零件尺寸和位置参数，在几何建模模块中建立各零件的几何模型，包括限位臂、限位滑块、限位盒等。限位臂是限位器中最主要的零件，限位臂的形状直接决定了车门开关过程中的挡位，以及开关门的力矩大小。由于受到限位盒尺寸的限制，为避免在运动过程中限位臂与限位盒之间出现运动干涉，限位臂的轨迹和形状会变得较为复杂。限位臂轨迹如图1所示，图1中A点为车门铰链的旋转中心，B点为限位臂的旋转中心，C点为限位盒内滑块的中心代表车身代表车门代表限位臂初始段的轨迹，作代表限位盒。车门铰链轴线与限位臂轴线距离车门铰链轴线与限位块中心距离夹角为138°。限位器的理想轨迹为复杂曲线，难以正常获取，而按照单元逼近法[6-10]，可以将限位臂轨迹划分为几段进行拟合。笔者根据车门的开关门角度将限位臂轨迹划分为若干段来获得其拟合轨迹。

▲图1 限位臂轨迹示意图

在确定好限位臂的轨迹及轮廓后，需要确定限位臂厚度、凹槽位置、凹槽深度等参数，并增加其它附属结构，最终建立限位臂模型。在建立装配关系前，需要建立一个固定不动的地面，代表相对不动的车身。地面与限位臂和车门均为旋转副连接，因此只需要在地面上在对应的位置建立两个坐标系，限位臂和限位盒通过这两个坐标系与地面装配。装配之后在Virtual.Lab Motion软件中定义装配体及各关键零件的结构参数，包括运动关系、惯性参数、力单元和接触单元等。限位器装配图如图2所示。

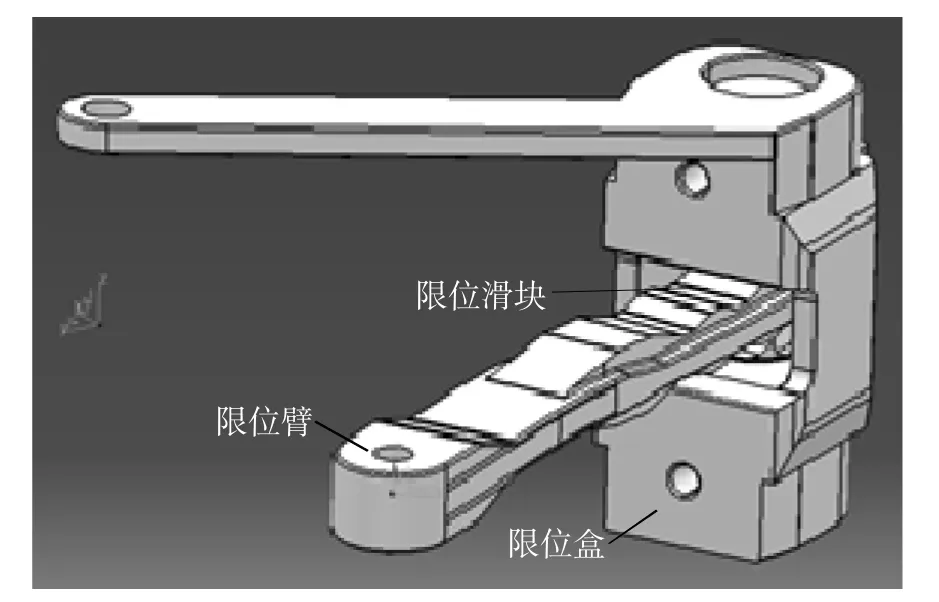
▲图2 限位器装配图

3 限位器多体动力学模型优化

3.1 限位器仿真

在初步建立的限位器模型基础上，进行限位器整体多体动力学仿真[11]。型号1限位器限位臂各挡位凹槽形状尺寸见表1。仿真工况为开门和关门两个工况，初始系统限位盒保持5 s静止，使限位滑块和限位臂充分接触，达到平衡状态，之后驱动限位盒以1（°）/s的角速度匀速转动。

关门和开门工况下，限位盒驱动扭矩随时间变化曲线分别如图3、图4所示。由图3、图4可知，最初5 s限位盒的静止状态已经使限位臂与限位滑块之间充分接触，达到了稳定状态。5 s时限位盒由静止突然开始匀速转动，因此该时刻会出现一个较大的驱动力矩，对于这一力矩，笔者不进行分析。

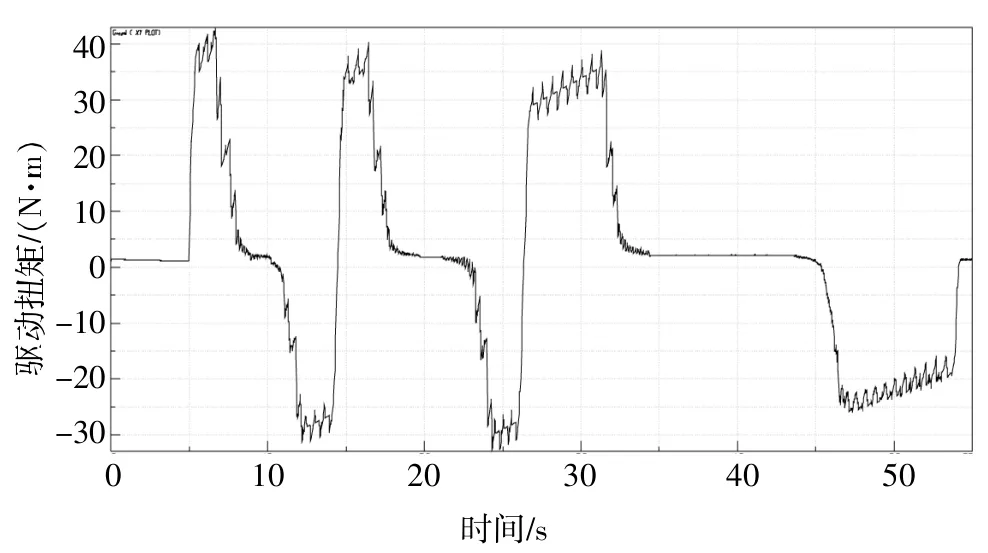
▲图3 关门工况限位盒驱动扭矩随时间变化曲线

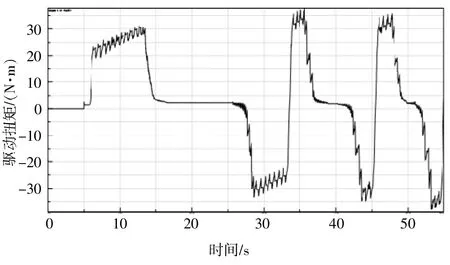
▲图4 开门工况限位盒驱动扭矩随时间变化曲线

图3、图4中，正扭矩表示需要推动限位器越过各挡位处凹槽的斜面，负扭矩表示凹槽的斜面会推动限位滑块自动滑入凹槽内。对于负扭矩，笔者不进行研究。从曲线中可以获得开关门过程中各挡位所需的最大扭矩，以及所对应的时间，并可推出对应的开关门角度，并设车门关闭时的角度为0°。表2为各挡位仿真结果。

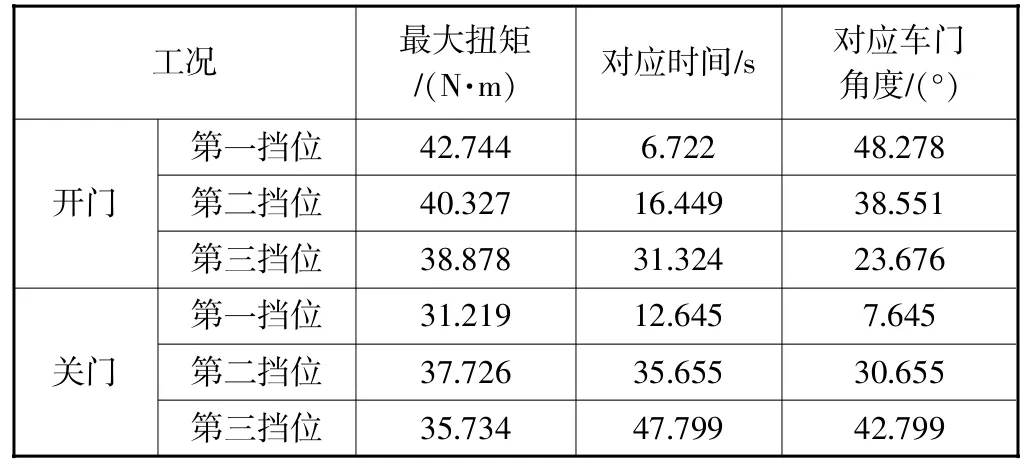
表2 各挡位仿真结果

最大扭矩出现时所对应的限位滑块和限位臂接触位置如图5所示，可见出现最大扭矩的位置均为斜面末端接近限位臂最厚位置处，此时弹簧长度最短，施加的压力最大，需要最大的扭矩来克服限位滑块与限位臂之间接触所产生的阻力。

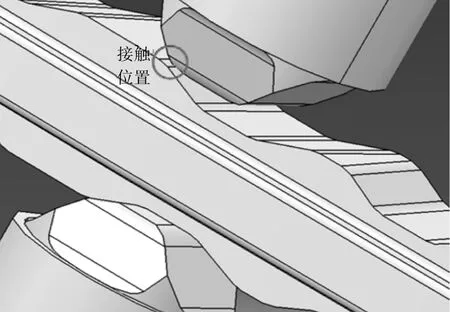
▲图5 最大驱动扭矩对应限位滑块与限位臂位置

3.2 限位器开关门扭矩试验

选取三款同类型且只有限位臂形状有一定差异的限位器，分别设为型号 1、 型号 2、型号3，每款限位器各5个，共对15个限位器进行试验。其中，型号2只有两个挡位，型号1和型号3均有三个挡位。限位器试件如图6所示。

测量时，先将限位滑块置于关门第一挡位的凹槽处，即使夹具初始位置在车门最大开启状态。推动限位器运动，推动过程保持缓慢且匀速。推过限位器关门第一挡位后，使滑块缓慢滑入第二挡位的凹槽中，通过表盘上的指针读取限位滑块通过关门第一挡位凹槽所产生的最大扭矩。依次类推，分别对限位器关门三个挡位和开门三个挡位进行测量，获得各挡位对应的最大扭矩值，并进行记录。

对每款5个限位器试件测得的各挡位扭矩数据求取平均值，见表3。

▲图6 限位器试件

表3 限位器各挡位扭矩测量平均值 N·m

3.3 仿真与试验对比

对三款限位器各挡位获得的仿真驱动扭矩，与扭矩试验测得的扭矩测量平均值进行比较，得到相对偏差，见表4。

表4 限位器各挡位仿真驱动扭矩与试验扭矩相对偏差

仿真扭矩和试验扭矩的相对偏差小于10%，表明仿真结果符合要求。由此可见，通过笔者建立的动力学模型及匀速旋转限位盒工况，可以获得较准确的限位器实际所需扭矩。

4 驱动扭矩影响因素分析

4.1 影响因素选择

针对影响驱动扭矩较大的因素，初选限位臂厚度H、凹槽深度D、斜坡角度β、斜坡顶部圆角半径R1及滑块上圆角半径R2这五个影响因素，如图7所示。

▲图7 驱动扭矩影响因素

为了判别初选因素是否会对驱动扭矩产生较大影响，采用控制变量法。为了尽量减小限位臂与限位盒之间的接触对驱动扭矩的影响，选择该接触产生的扭矩与限位器驱动扭矩比值最小的关门第二挡位作为仿真工况。

通过控制变量法对初选的影响因素进行仿真对比，最终判断H、β、R1和R2会对驱动扭矩产生较大的影响，并做进一步分析。由于D不会对驱动扭矩产生较大影响，因此笔者不再进行研究。

4.2 正交设计与分析

确定的影响因素有H、β、R1和R2四个，由于分析的因素较多，如果对各因素的所有水平都进行全排列搭配组合，那么所要进行的仿真数量将非常庞大。而正交设计是针对多因素试验的一种有效解决办法，可以在全排列试验中挑选出有代表性的部分组合，且仍然保持着均匀和整齐的特点，可以有效减少组合数量，但仍能从中分析获得各个因素的影响规律[7-9]。

确定研究的因素数量为四个，各因素的水平数量和水平范围则根据限位器对于各参数的限制范围，以及进行试验的限位器试件所使用的参数数值确定，以方便后续通过试验验证分析结果。最终确定的因素水平表见表5。

表5 因素水平表

根据正交表的设计规律[10]，试验需要的正交仿真组别数为16组，见表6。

继续使用前文所述的限位器模型和仿真工况进行仿真，获得关门第二挡位置处的驱动扭矩。凹槽深度D保持2 mm不变，其余参数数值根据试验正交表对应的组合逐一调整后进行仿真，基于获得的驱动扭矩曲线得到驱动扭矩的最大值，并最终得到16次仿真试验的扭矩，见表7

通过对正交设计获得的仿真结果进行直观分析，可以获得各因素对于仿真结果的影响趋势。将各个因素每个水平对应的仿真驱动扭矩进行相加，如将所有的β为8°的仿真驱动扭矩进行相加，记作K1，则K1=14.059+15.230+15.162+15.763=60.214 N·m。 同理，β为14°的结果记作K2。依次类推，还可以获得其它因素对应的K值。将获得的K值除以各水平出现的次数，得到平均值，记作k。各因素k值见表8。

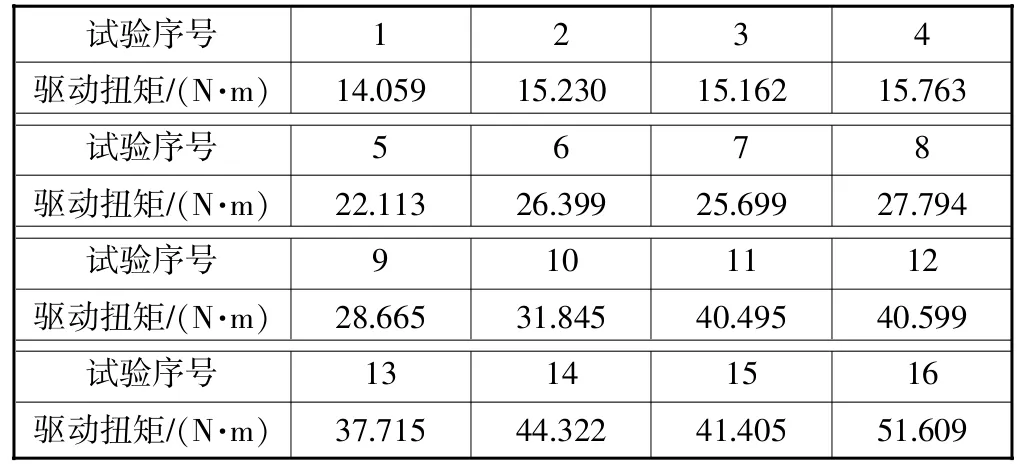
表7 仿真试验驱动扭矩

表8 各因素k值 N·m

一个因素k值的变化反映了该因素各水平对于仿真结果的影响情况，可以通过k值获得各水平的影响趋势图。各因素对驱动扭矩的影响如图8所示。

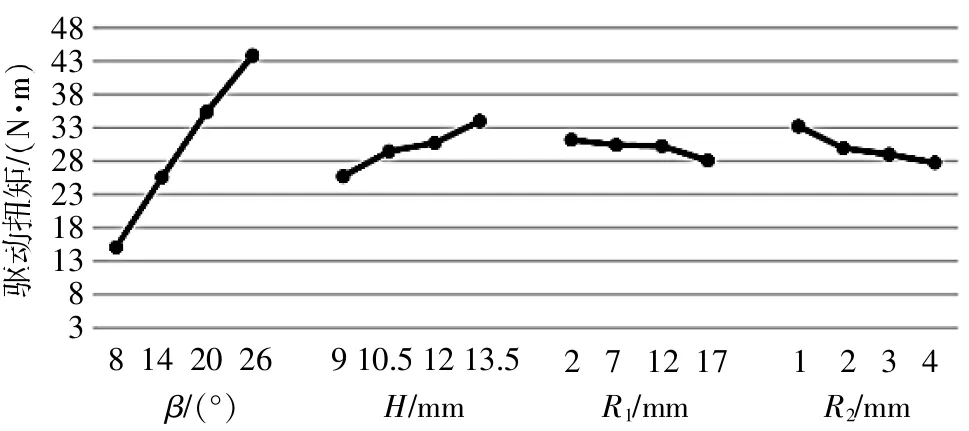
▲图8 各因素对驱动扭矩的影响

从图8中可以发现，斜坡角度对于驱动扭矩的影响最大，而限位臂厚度、斜坡顶部圆角半径和滑块圆角半径的影响情况基本相近。

4.3 回归分析

通过回归分析，可以确定仿真结果的回归方程，对不同参数对应的驱动扭矩结果进行预测。

4.3.1 因素水平编码

因素水平编码将各因素的水平进行线性变换，如对斜坡角度β进行线性变换，编码记作Z1，变换式为：

式中：β0为斜坡角度四个水平的平均值；Δβ为斜坡角度变化间距。

由式（1）求得斜坡角度 β 为 8°、14°、20°、26°时对应的 Z1编码值依次为-1.5、-0.5、0.5、1.5。

与式（1）相类似，其余因素的变换式为：

式中：H0为限位臂厚度四个水平的平均值；ΔH为限位臂厚度变化间距。

式中：R10为斜坡顶部圆角半径四个水平的平均值；ΔR1为斜坡顶部圆角半径变化间距。

式中：R20为滑块圆角半径四个水平的平均值；ΔR2为滑块圆角半径变化间距。

4.3.2 一次回归正交表

将各因素对应的编码代入原试验正交表，获得一次回归正交表及仿真扭矩，见表9。

表9 一次回归正交表及仿真驱动扭矩

一次回归方程为：

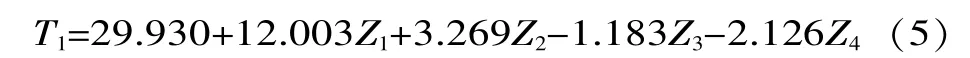
根据式（1）～式（4），计算并代回式（5），得：

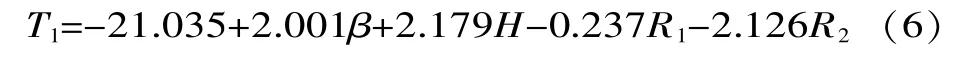
4.3.3 一次回归方程验证

为了验证方程的准确性，并判断方程是否能够预测限位器实际的驱动扭矩值，笔者将进行驱动扭矩测量试验的三款限位器各挡位参数代入一次回归方程，获取驱动扭矩值，然后同实际测得的驱动扭矩值进行比较，得到回归方程计算值与试验测量值的相对误差，见表10。

从对比结果可以发现，回归方程计算得到的驱动扭矩值与试验测量值在某几个挡位关门动作时存在较大的误差，且出现误差较大的挡位其斜坡角度均较大，且不小于20°。而其余挡位的回归方程计算值与测量值的相对误差均较小，在8%以下。分析原因，可能是因为在斜坡角度较大时，限位器驱动扭矩的变化随斜坡角度的变化已经不满足线性关系。

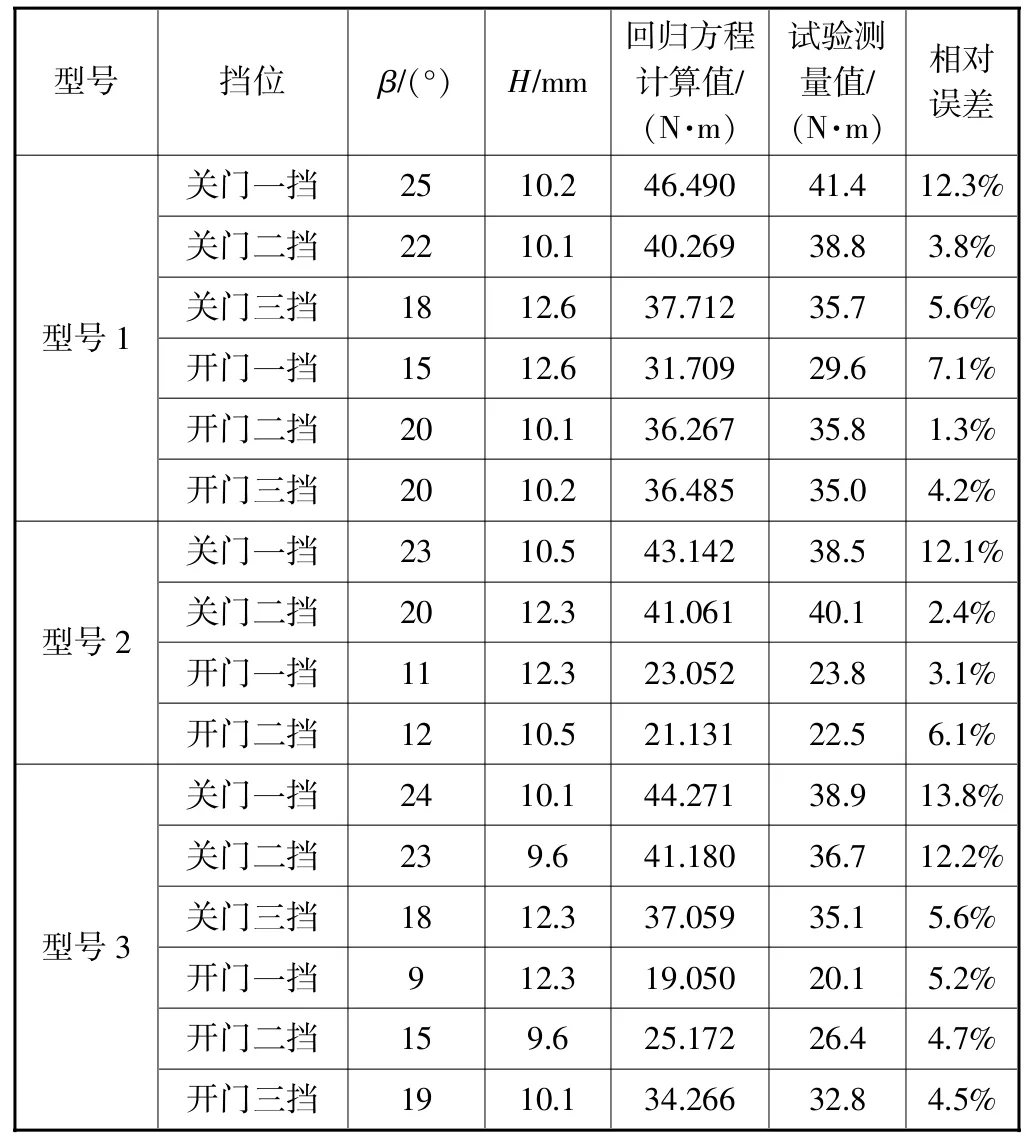
表10 驱动扭矩回归方程计算值与试测量值相对误差

为了修正在斜坡角度较大时引起的误差，笔者针对斜坡角度β不小于20°的情况，对一次回归方程进行修正，重新获得一个适用于斜坡角度β不小于20°的一次回归方程。为此，重新选取大角度的斜坡角度水平，再次进行正交设计和仿真。选择的斜坡角度β水平为 20°、22°、24°、26°，其余因素的水平数和水平数值保持不变，重新获得的一次回归正交表和仿真获得的驱动扭矩值见表11。

求得新的一次回归方程为：

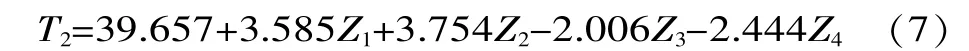
即：

对斜坡角度β不小于20°的几个挡位重新进行比较，得到新回归方程计算值与试验测量值的相对误差，见表 12。

根据仿真经验，从对比结果中可以发现，计算值和测试值的相对误差有了明显降低，均在10%以内。其中型号3的关门第一挡位驱动扭矩偏差为10.0%，较大，这可能是由于型号3的实际限位臂模型与仿真使用的限位器模型存在一定差异引起的。

最终获得限位器驱动扭矩的数学模型为：

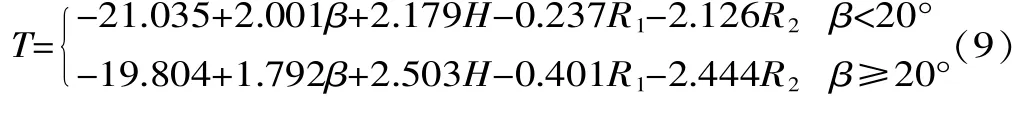
表11 新一次回归正交表及仿真驱动扭矩

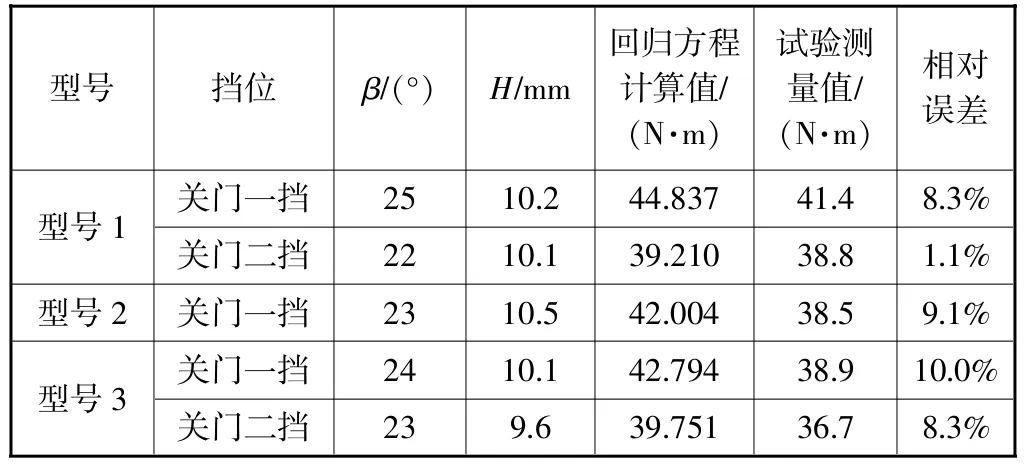
表12 驱动扭矩新回归方程计算值与试验测量值相对误差

5 结论

根据实际限位器模型和动力学仿真要求，建立了限位器动力学模型。通过限位器驱动扭矩测量试验与仿真结果相对比，验证了限位器动力学模型和仿真方法的准确性。

着重讨论了限位臂厚度、斜坡角度、斜坡顶部圆角半径和滑块圆角半径对驱动扭矩的影响，通过正交设计和回归分析，建立了限位器扭矩的数学模型，并初步验证了回归方程的准确性。