基于改进A* 算法的智能仓库移动机器人的路径规划

王海玲*

（厦门大学嘉庚学院，福建厦门，363105）

引言

机器人路径规划是滑动机器人研究的热点问题，可描述为在有障碍物的环境下，寻找一条从给定起点到指定终点的运行路径，在整个过程中必须安全、无碰撞地绕过所有障碍物，且尽量使所走路径最短（或者所花费时间最小、成本最少等）。目前，应用于机器人运动规划的方法有Dijkstra算法、A*算法等传统算法及遗传算法等智能算法。Dijkstra算法可保证搜索到全局最优路径，但是具有一定的盲目性，当节点增多时，该算法所搜索到的节点很多，效率低。遗传算法在寻找全局最优解的过程中，是一个随机搜索的过程，当节点增多时，搜索时间较长，且易出现早熟的现象。A*算法是一种启发式搜索算法，搜索具有一定的方向性，实现简单，搜索效率高，已被广泛应用，详见参考文献[1-5]。顾辰[6]考虑到现实机器人的体积，采用基于优先级的子节点生成策略得到了机器人行走时突遇未知障碍物时路径规划问题，但是并没有考虑到转弯角度和方向。李伟光等[7]有合转弯因素，采用删除边的方法研究了AGV路径规划问题，但是计算实际路径时还是用直线段代替。王殿君[8]考虑了旋转方向和旋转角度研究了室内机器人路径规划问题，但是并没有减少机器人的路径长度及转折角度。王红卫等[9]提出了一种平滑 A*算法，减少了不必要的路径节点并减少了路径长度和转折角度，但是只是在原有的路径点上处理，路径长度和转折角度减少量有有。孙炜等[10]提出了另一种改进的A*算法，进一步减少滑动机器人总的路径长度和转折角度，但是没有进行平滑处理。本文在前面文献基础上，通过修改评价函数，既考虑转弯因素又考虑转折次数，使得规划出的路径更优化、更平滑。

1 系统建模

众所周知，滑动机器人工作环境的信息建立是路径规划中十分重要的一步。图1是智能仓库系统简图（一个方格代表一个货架，空白箭头处表示机器人行驶路线）。本文采用棋盘式环境建模，首先将每一个货架视为棋盘的一个方格，方格大小一致，将不规则区域填充为障碍物，使其成为标准的棋盘。然后以货架、机器人所在空闲区域、障碍物为方格，构造棋盘如图2（以11行11列为例）。假设同一行或同一列的机器人，若他们之间没有障碍物，则可按原计划执行的线路行走。若突遇障碍物，则会发生碰撞导致失去原来的行驶路线。于是产生如下问题：（1）突遇障碍物时如何行驶？（2）如何规划一条从起点到终点的最优路径？

图1 智能仓库简图

图2 棋盘式地图模型

假设如下：

（1）S，T分别为起点和终点,i为中间节点（为障碍物），加粗边框方格为障碍物所在方格，白色方格为无障碍物方格；

（2）障碍物边界是在实际边界的基础上加一个滑动机器人安全距离得到的，即把机器人看作一个质点；

（3）机器人滑动方向的任意的。

本文的目的是找到一条从起点S到终点T的最优无碰撞路径。

2 突遇障碍物时行驶路线规划

按原计划执行的线路在i处突遇障碍物，传统的 A*算法在生成与其相邻的 8个子节点时并没有考虑优先行走顺序，本文考虑优先级的子节点生成策略，把所有与当前节点i相邻的水平、竖直、对角线的8个节点按照先水平，后竖直，再对角线分为三级（如图2）。

（1）如A为障碍物节点，则不生成包含iF，iH的路径；

（2）如B为障碍物节点，则不生成包含iE，iG的路径；

（3）如C为障碍物节点，则不生成包含iE，iF的路径；

（4）如D为障碍物节点，则不生成包含iG，iH的路径。

在原始计划S-O-i-T的路径过程中，若到i为障碍物，认为机器人当前位置i及当前朝下的位置A为

未知障碍物，则根据子节点优先级，在B处优先选择E，再E到N，依次进行，最后到终点T。

3 转弯因素及转折角度计算

第二部分知道，在i处突遇障碍物，在i的前面B处要迫使机器人改应原来的行驶方向，按子节点优先级可行驶至 N，但是在N的前方和右方都遇到障碍物，这时如何行驶？是沿着黑色折线行驶到M还是走弧线到M？如有是沿着弧线行驶，则转弯的角度和旋转方向如何？由于机器人在转弯时要减速并调整姿态，在实际运行中，转折次数的多少、转折角度的大小对规划出来的路径起着至关重要的作用，为此，引入转弯因子及转折角度等参数。

在图2中，令NK、MK与水平线的夹角分别记为α1，α2，MK与 NK的延长线夹角记为θ，由θ的值来判拓展节点是否发生转向。

若θ=π，则不转向，按原计划的线路行驶；

若θ≠π，则发生转向，存在拐点。把拐点及拐点的父节点提取出来，这样就得到只剩起点、拐点、终点的曲线，而且旋转的方向及旋转角度大小可以由θ来决定。

设 N、K、M 的坐标依次为（x1,y1）, （x2,y2）, （x3,y3）,令θ=α1-α2，则

当θ＞0, y3≥y2, y2≥y1时，右转θ；

当θ＞0, y3≤y2, y2≤y1时，右转θ；

当θ＞0, y3≥y2, y2≤y1时，左转180°-θ；

当θ＞0，y3≤y2, y2≥y1时，左转180°-θ；

当θ＜0，y3≥y2, y2≥y1时，左转-θ；

当θ＜0，y3≤y2, y2≤y1时，左转-θ；

当θ＜0，y3≥y2, y2≤y1时，左转180°＋θ；

当θ＜0，y3≤y2, y2≥y1时，左转180°＋θ。

通过计算θ，即可判定在行驶过程中有没有发生转弯及转弯的角度大小，进而可以得到一条从起点到终点的考虑旋转方向和角度的最优路径。

4 启发函数的构造

A*算法是一种典型的启发式搜索算法，它从起始点开始，根据估计代价选择价值最低的作为下一个拓展节点，直到将目标点拓展进来为止，获得最终最优路径。因此 A*算法的关键在于选择一个合适的启发函数。传统的A*算法的启发函数一般为：

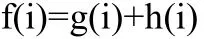
其中，f(i)是当前节点i的估计函数，g(i)是起点到当前节点 i的实际费用，这个费用是可以算出来的。h(i)是从当前节点到终点最小费用的估计，一般采用欧几里得距离、曼哈顿距离、切比雪夫距离等进行计算，但是实际在选择最优路径时还受到方向的影响，仅以距离作为约束条件显示不是最优的，为此我们加入方向因素来考虑，现修改启发函数为：

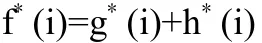
g(i)为修改后的当前节点的实际费用，若θ=π,则没有转向；若θ≠π，则发生转向。l,L分别为当前节点和起始节点到终点的欧几里得距离，l,L比值越接近 1，说明当前接近越接近目标点，α分别为当前节点与后续节点的矢量和起始节点跟终点的矢量的夹角，θ为上文中的夹角，的比值越接近1，说明选取的节点路径方向越接近终点方向。

5 算法流程

（1）初始化设置，设O为已拓展列表和C为待拓展列表；

（2）令S∈O，C=φ，检查O是否为φ，若为φ，则搜索失败，否则转（3）；

（3）选O中最小的f(.)节点i作为拓展，从O中删除，放入C中，并判断i是否为目标点，若是，则转（5），否则转（4）；

（4）判与i相邻的节点j是否在O表中。作如下操作：若在，则判j的当前g值是否比原来小，若是，则把i作为j的父节点，重新计算j的新的f,g,h；否则，不作任何操作。若不在，则把j添加到O中，并将i作为j的父节点，计算j的f,g,h值，转（3）；

（5）从 j开始，用回溯法输出起点到目标点的最优路径。

6 有束语

（1）通过棋盘式的建模方式，构建了仓储的环境模型；

（2）通过障碍物所在节点的优先级，解决了机器人行走时突遇障碍物的行驶路线问题；

（3）通过考虑旋转方向和旋转角度，引入了新的评价函数计算方法，使规划出的路径更加合理、更加优化。