最小断点集的简化计算与组数扩充
2018-09-19,
,
(1.国网四川省电力公司电力科学研究院,四川 成都 610041;2.国网成都供电公司,四川 成都 610041)
0 引 言
计算最小断点集(minimum break point set,MBPS)是复杂环网方向保护整定的第一个步骤。近年来,国内外学者在这方面做了大量的研究。文献[1-4]基于图论的相关方法计算MBPS,这种方法需要找出网络的有向简单回路,因此当电网规模较大时计算量将会相当大。文献[5]提出了保护的主后备配合关系,通过对保护配合依赖度的动态调整计算MBPS。文献[6]在文献[5]的基础上,将保护的配合关系用一个0-1矩阵表示,通过对矩阵的行列化简运算计算MBPS。上诉两种方法不用寻找网络的有向简单回路,计算量较小,但当网络规模较大时,矩阵维数过大,计算较为繁琐,并且不能得到多组最小断点集。文献[7]将在计算MBPS前,通过一系列原则对问题进行简化,降低计算复杂度。文献[8]通过网络简化和有向图化简计算MBPS,但需要多次进行网络拓扑分析。
通常情况下,电网会有多组基数相同的MBPS,在进行整定计算时,整定计算人员需根据电网的实际情况,选择一组最合适的MBPS[9]。因此,在计算MBPS的过程中,应尽量得到多组基数相同且最小的MBPS,以方便工程选择。在现有的算法中,通过图论和智能算法可求得的MBPS组数较多,但计算复杂。通过保护配合关系计算MBPS的算法较为简单,但得到的MBPS组数较少。于是需在算法简单性和MBPS组数之间找到平衡点。首先通过割节点将电网分割成多个互不关联的连通子网,各个子网内MBPS的计算互不影响,再运用保护配合关系,形成各个子网的保护配合矩阵,通过矩阵化简并行计算各个子网的MBPS,然后根据MBPS的分布规律,对子网MBPS的组数进行扩充,最后将各个子网的MBPS进行组合便可得全网的MBPS。
1 电网分割
通常情况下,电网是由多个互不关联的连通子网组成,子网间不存在回路。因此,各子网计算MBPS互不影响。将电网分割后,将降低计算量。
为简化电网分割,首先需要对电网进行简化处理。电网中大量存在两个节点之间连接多条线路的情况,称之为平行线路,将这些平行线路用单回线代替可降低电网分割计算量[8]。另外,对于终端线路,无法形成回路,因此将其作为单独的子网处理,在进行电网分割前,首先将其分离。
找到电网的割节点,便可对电网进行分割,采用文献[10]的方法通过广度优先搜索技术寻找割节点。该方法基本思路为:消去与节点相连的支路,然后从余下的节点出发,若搜索到的节点数目与网络节点数不相等,则说明该节点为割节点。
在割节点处断开电网,即可得到多个互不关联的连通子网。
2 子网MBPS计算
计算出各个子网的MBPS是算法的核心部分,这里采用保护配合矩阵来计算子网MBPS。
2.1 保护配合矩阵
图1为一简单的不可再分割的连通子网。

图1 子网
图1所示子网保护间的配合关系可以用一个矩阵表示,A=(aij),称其为保护配合矩阵[6]。其中A为n阶方阵,n为保护的个数。如果保护i是保护j的后备保护则aij=1,否则为0。所示网络的保护配合矩阵A为

(1)
2.2 保护配合矩阵化简原则
为降低计算的复杂度,在计算MBPS之前对保护配合矩阵进行化简。
根据保护之间的配合关系可形成保护配合关系有向图[8],有向图中的顶点代表保护,有向边表示保护间的配合关系,有向边的方向为从后备保护指向主保护。因此计算MBPS可转化为找出有向图的最小反馈点集,以断开保护组成的所有有向回路。由此可将有向图的化简原则用于MBPS的计算中,为保护配合矩阵化简。若保护i仅有一个后备保护j,即保护配合矩阵中的第i列只有第j个元素为1,其他都为0,则可将保护i与保护j合并。矩阵操作为:将第i列加到第j列,然后删除第i行和第i列;若保护i仅有一个主保护j,即保护配合矩阵中的第i行只有第j个元素为1,其他都为0,则可将保护j与保护i合并,矩阵操作为:将第i行加到第j行,然后删除第i行和第i列。
对于平行线路,如图1所示的保护3、4、5、6平行线路保护集,由于相同节点上的两个保护配合关系一样,因此可以合并,将平行线路等效成单回线处理。如图1上的保护3和5、保护4和6。矩阵操作为:分别删除平行线路两个节点上其中一个保护所对应的行和列。对于图1所示网络,可删除其保护配合矩阵的第3行、第3列、第4行、第4列。
2.3 子网MBPS计算方法
若某个保护的后备保护越多,则该保护越有可能被选为断点。计算子网MBPS的核心思想就是通过判断后备保护的数量选择断点。
定义1:定义保护j的后备保护数量为保护j的配合后备依赖度(backup dependency,BD)。
定义2:定义保护i的主保护数量为保护i的配合主依赖度(primary dependency,PD)。
在得到保护配合矩阵后,便可按式(2)求出每个保护的BD和PD。
(2)
式中:N为网络中保护的总数;Aij为保护配合矩阵第i行第j列的元素。
计算子网MBPS步骤如下:
步骤1:根据子网中保护的主后备关系形成保护配合矩阵A。初始化断点数组S。
步骤2:对保护配合矩阵进行化简。
步骤3:计算每个保护的PD,若某保护的PD为0,则删除保护配合矩阵中该保护对应的行和列。重复此过程直至矩阵无法进行删减。
步骤4:计算每个保护的BD,将BD最大的保护选为断点,存入断点数组S,并删除该保护对应的行和列。
步骤5:重复步骤3和步骤4直到矩阵中的所有保护都被消去。
步骤6:搜索数组S中的保护,若有平行线上的保护,则将与之合并的同节点上的保护存入S中。
3 子网MBPS组数的扩充
按照所提出的方法,可得到子网的一组MBPS。而下面将阐述在一组MBPS的基础上得到多组MBPS的方法。
3.1 根据独立支路扩充
电网中存在许多无分支线路,如图2所示,保护1和2所在的线路、保护3和4所在的线路以及保护5、6、7、8所在的线路都为无分支线路。若MBPS中的一个断点保护所在的有向回路包含无分支线路上的保护,且该无分支线路包含两个以上的保护,则可用有向回路中处于该无分支线路上的另一个保护替代原保护作为断点。对于图2所示电网,若求得其一组MBPS为{1,3,5},而保护5和7处于一条有向回路,则将保护5用保护7替代可得另一组MBPS{1,3,7}。
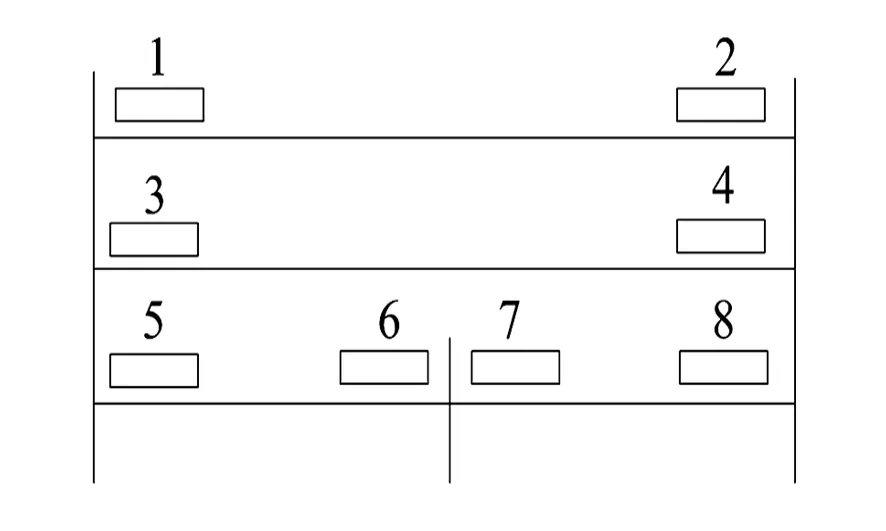
图2 无分支线路
3.2 根据MBPS对称分布特性扩充
文献[11]证明MBPS的分布具有对称特性,即对于子网的MBPS,其中的每个断点保护所对应的同一条线路上的对端保护所构成的保护集合也是该子网的MBPS。
如图3所示,保护1和3构成该子网的一组MBPS,这两个保护所对应的同一条线路上的对端保护2和4同样为该子网的一组MBPS。
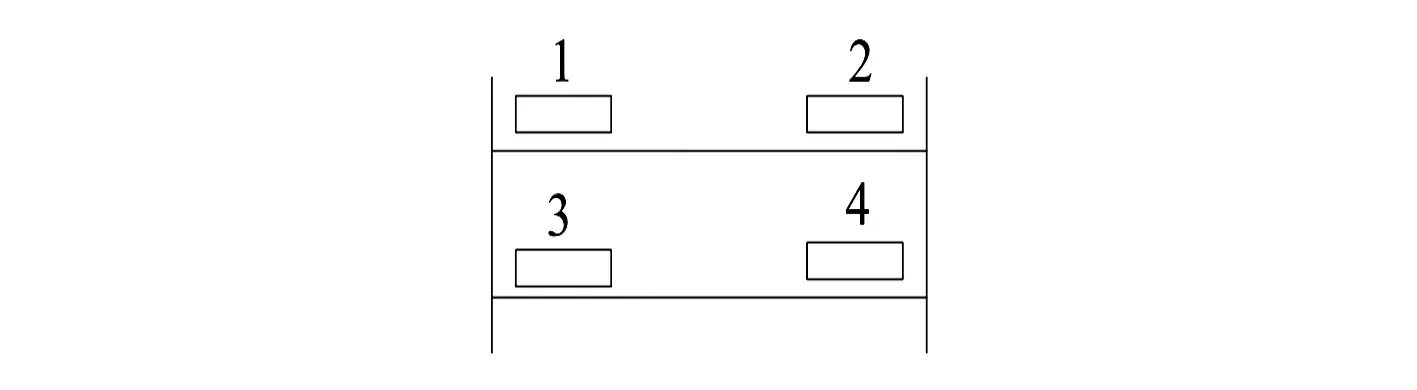
图3 MBPS的对称特性
根据MBPS的对称分布特性,取原有的MBPS中的每个断点保护同线路上的对端保护,即可得到另一组完全不同的MBPS。
4 全网MBPS计算步骤
全网MBPS的计算步骤如下:
步骤1:简化电网,找出割节点,在割节点处将电网分割成若干个子网。
步骤2:形成各个子网的保护配合矩阵,并进行化简,根据第2.3节的方法计算各个子网的MBPS。
步骤3:根据独立支路对各个子网的MBPS进行扩充。
步骤4:根据MBPS对称分布特性对各个子网的MBPS进行扩充。
步骤5:将各个子网的MBPS组合起来便可得到全网的MBPS。
5 算例分析
算例电网如图4所示。
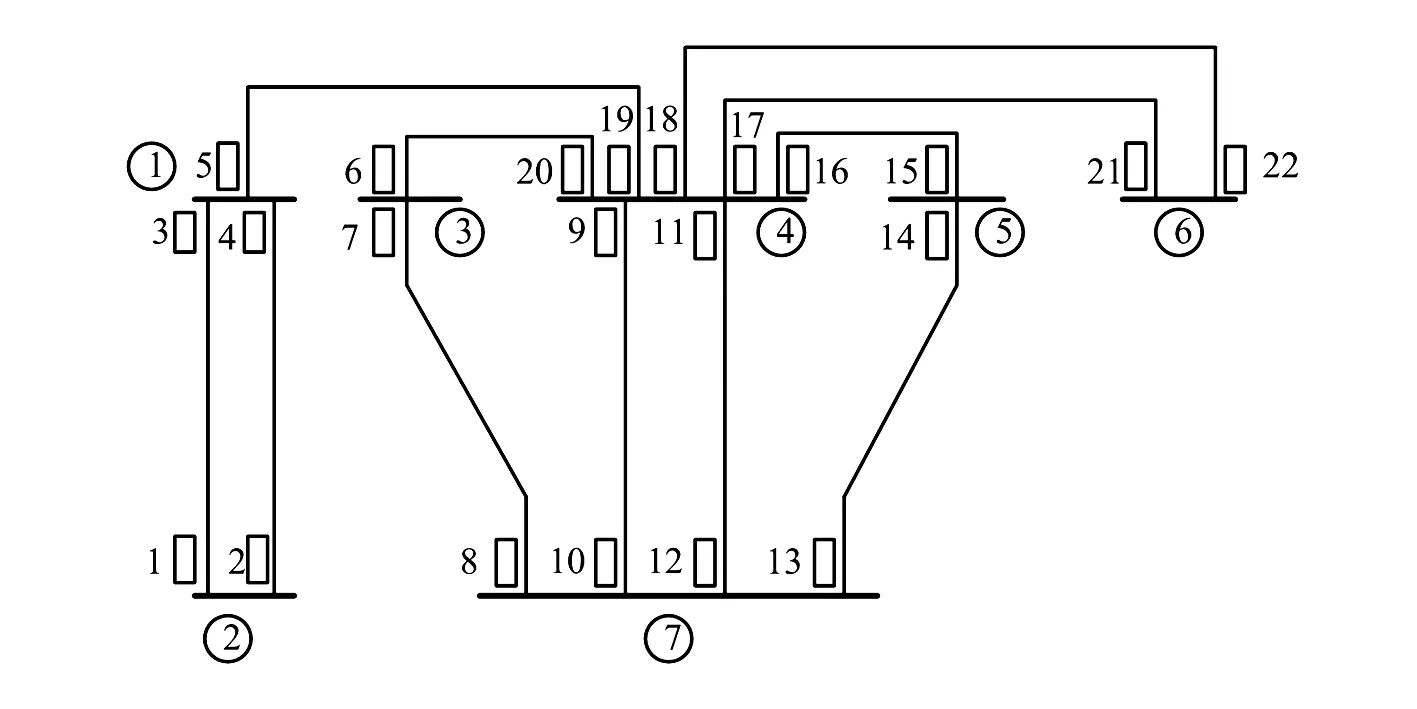
图4 算例电网
采用广度优先搜索技术得到电网的割节点为节点1和节点4,在割节点处将电网分割成4个互不关联的连通子网,如图5所示。

图5 分割后的电网
在这4个连通子网中,子网C为单回线路构成的网络,在未分割前的电网中,子网C为非末端线路,该线路两端保护的主保护处于其他子网中,因此确定了其他子网的整定顺序,就可确定该线路两端保护的整定顺序。故子网C的两个保护不作为断点。
子网A和子网B为平行线路,选择平行线路的一端作为MBPS,其MBPS分别为{1,2}和{18,17}。根据MBPS的对称分布特性进行扩充,最后得到子网A的MBPS为{1,2}和{3,4},子网B的MBPS为{21,22}和{18,17}。
子网D较为复杂,根据所提方法求得其MBPS为{8,10,12,13}。保护8、7、6、20和保护13、14、15、16所在的线路为无分支线路。保护6和8处于一条有向回路中,保护13和15处于另一条有向回路中,因此分别将保护6和13用保护8和15替代得另外3组MBPS:{6,10,12,13}、{8,10,12,15}、{6,10,12,15}。再根据MBPS对称分布特性可得另外4组MBPS:{7,9,11,14}、{20,9,11,14}、{7,9,11,16}、{20,9,11,16}。可以看出,一组MBPS通过所提方法进行扩充,可得8组MBPS。
将各个子网的MBPS组合起来便可得全网的MBPS。通过排列组合,采用所提方法,最终可得32组算例电网的MBPS。经过所提方法对MBPS进行扩充后,可极大地增加MBPS的组数,有利于工程选择。
6 结 语
在MBPS的简化计算和MBPS组数的扩充两方面进行了研究。将电网分割成互不关联的连通子网,然后通过保护配合矩阵计算各个子网的MBPS,在求得子网的MBPS后,对其进行扩充,得到子网的多组MBPS,最后将各个子网的MBPS组合起来得全网MBPS。通过保护配合矩阵的化简,简化了子网MBPS的计算,而MBPS的扩充又增加了MBPS的组数,为实际工程应用提供了更多的选择。
