基于单神经元PID控制的双旋翼实验平台系统研究

闻 新，陈 镝，乔 羽

(1.沈阳航空航天大学 航空宇航学院，沈阳 110136；2.燕山大学 经济管理学院，河北 秦皇岛 066004)

传统PID是一种比较实用的线性控制，具有结构简单、参数意义明确、易于实现等优点，现在仍是工业过程控制中最常用的控制器。但是传统PID很难实现参数的实时调整，对被控对象有很强的依赖性,而且现实中参数时变系统或非线性系统越来越多，控制对象越来越复杂，传统PID很难满足系统要求[1]。神经网络具有很强的学习记忆与自适应能力，可以处理难以描述的复杂问题，将神经网络和PID结合在一起能够弥补传统PID的不足之处[2]。所以近几年来神经网络PID逐渐取代传统PID，已广泛应用到各个领域。袁静[3]等将基本BP神经网络算法、粒子群算法和PID控制器三者结合起来，得出一种改进的神经网络复杂PID控制方法，并将其应用到多自由度机器人控制系统中进行仿真，降低了系统的稳态误差，优化了系统的动态过程。常静[4]基于BP神经网络优化算法，设计了一种新型的船舶模糊PID自动舵，与传统自动舵相比提高了自动舵的控制精度、应变性能和可靠性。程启明[5]等将基于模糊径向基函数的神经网络PID控制应用到球磨机中并进行仿真，表明模糊径向基神经网络能够有效地解决球磨机的复杂控制问题。扈宏杰[6]等提出了一种基于RBF神经网络的、结构简单的、稳定的PID直接自适应控制方法，并对位置随动系统进行仿真，得出该方法的鲁棒性和跟踪性能均优于经典PID方法的结论。龙晓林[7]等提出一种基于优化BP神经网络结构的PID控制器，采用优化的BP算法可以避免神经网络陷入局部极小点，并且加快了网络的训练速度。王春晨[8]等将BP神经网络PID控制应用到气体混合配比系统中进行仿真实验，证明控制器在气体混合配比系统中具有良好的控制性能。李卓[9]等提出一种基于BP神经网络的模糊自适应PID控制器并进行仿真实验，证明该控制器对模型、环境具有较好的适应能力和较强的鲁棒性。屈毅[10]等针对大滞后、大惯性的温室温度控制系统，采用RBF神经网络与常规PID控制系统结合构成的控制策略，实现了更好的控制效果。丁军[11]等人针对制药厂发酵罐温度控制回路的大滞后、大惯性的特性，采用可调参数少、易于整定、控制输出平稳的单神经元网络PID控制，在实际生产中取得了良好的效果。

随着智能控制的发展，像模糊PID、遗传算法PID等智能PID控制方法不断出现，并逐渐成为现阶段直升机发动机控制、姿态控制、悬停控制等领域的重要控制方法[12-13]。因此，本文采用单神经元控制与PID控制相结合得到的单神经网络PID控制，通过对双旋翼实验平台进行控制实验，与传统PID进行结果比较来研究单神经网络PID的实际控制性能。单神经网络相对上述神经网络PID来说比较简单。单神经网络PID控制中神经元的权值与PID控制的参数一一对应，以PID控制的三个参数的偏差为神经元输入，利用自适应学习算法来实时调整PID控制的参数。既保留了传统PID简单、易于实现等优点，又具有神经网络学习记忆和自适应的能力。

1 建立数学模型

1.1 实物模型

本文进行控制比较所选用的被控对象为双旋翼实验平台[14-15]，即双转子直升机模型。双旋翼实验平台是一个多输入多输出、高阶、多变量且具有强交叉耦合的非线性复杂系统[16]。如图1所示，模型主要由底座、支撑杆、两个旋翼、横梁、平衡锤、传感器和电机组成。相对于地面水平的前转子主要影响围绕俯仰轴的运动，尾部旋翼主要影响围绕偏航轴线的运动。

图1 双旋翼实验平台实物图

1.2 动力学方程

根据图1的实际模型画出双旋翼实验平台的简单受力图如图2所示。

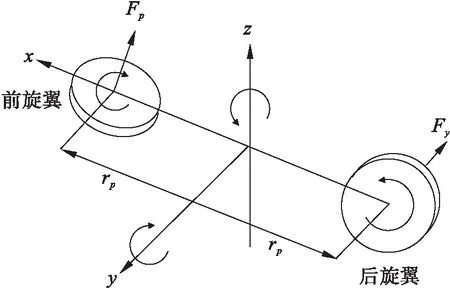
图2 双旋翼模型简单受力图

根据图2构建双旋翼的动力学方程为

(1)

其中作用在俯仰和偏转轴上的扭矩为

上述方程中的参数定义如下：Jp是关于俯仰轴的总转动惯量，Jy是关于偏转轴的总转动惯量，Dp是关于俯仰轴的阻尼，Dy是关于偏转轴的阻尼，Ksp是关于俯仰轴的刚度，Kpp是俯仰转子的转矩推力增益，Kpy是作用在来自偏航转子的俯仰上的交叉扭矩推力增益，Kyy是偏转转子的转矩推力增益，Kyp是作用在来自俯仰转子的偏航上的交叉扭矩推力增益，Vp是施加到俯仰转子的电压，Vy是施加到偏航转子电机的电压。

1.3 线性状态方程描述

双旋翼模型的控制器是通过调节电机的电压来控制旋翼的角度，所以定义模型的状态向量、输出向量和输入向量为

根据动力学方程式(1)，得出双旋翼模型的状态方程为

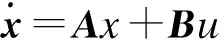
y=Bx+Du

(2)

其中状态控制矩阵为

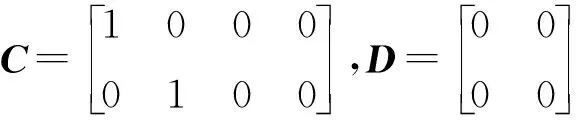
由真实实验得出的状态控制矩阵中的参数结果如表1所示。

2 单神经网络PID控制

2.1 数字PID控制

在单片机或者计算机做控制器时，原来连续的PID控制必须用离散的数值计算[17]。设采样时间为T，可用如下关系近似替代PID控制算法。

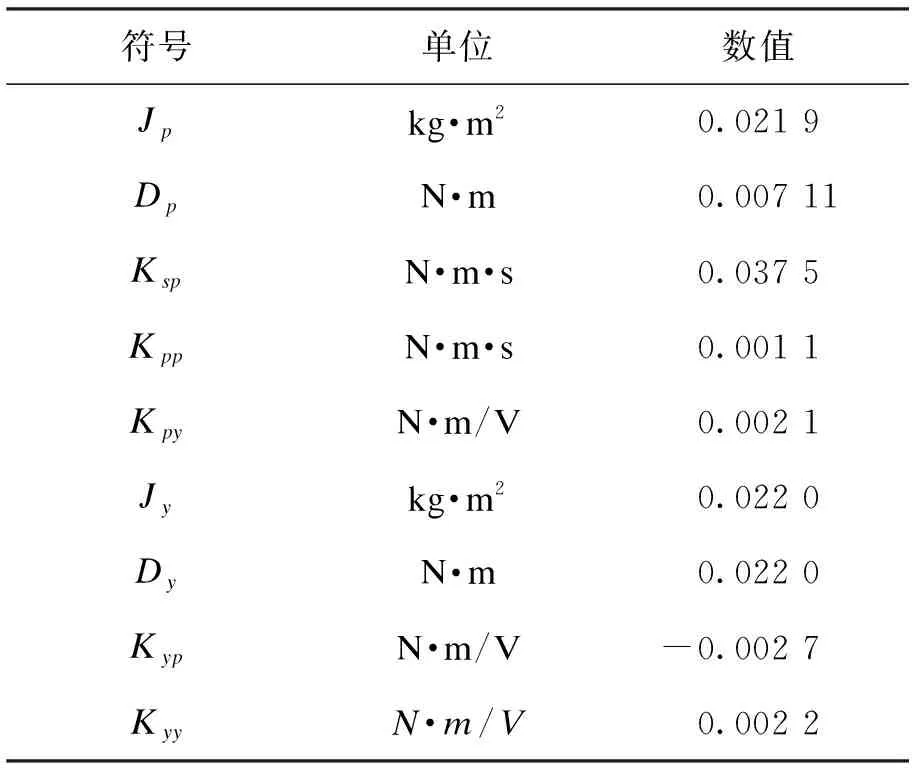
表1 数学模型参数值

由上式可得增量形式的PID控制算法：

其中Δu(k)=u(k)-u(k-1)。

2.2 单神经网络PID控制

本文所使用的单神经网络PID控制结构如图3所示。将PID控制器视为一个特殊神经网络，这里称之为单神经元PID网络，该网络是一个单输入单输出的网络。其隐含层为三个神经元，比例、微分、积分函数作为这三个神经元的激活函数，输出层为求和函数，比例、微分、积分增益作为隐含层与输出层连接权值。

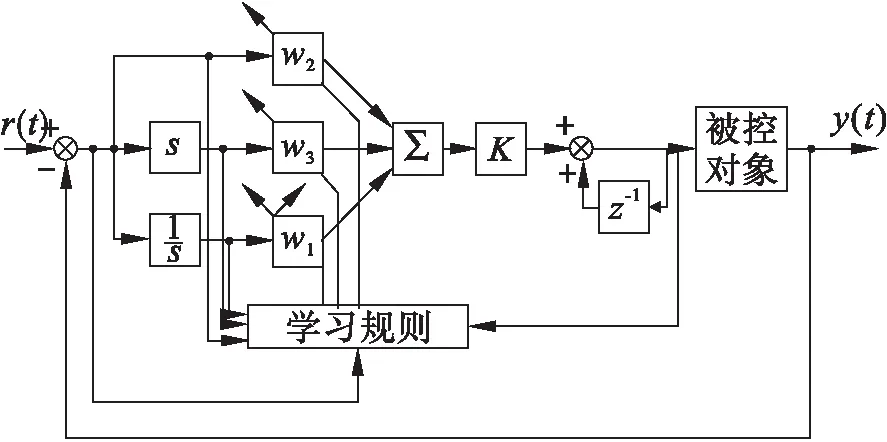
图3 单神经网络PID控制结构图

单神经网络的输入为系统参考输入与实际输出直接的误差e(t)，输出为控制量u(t)。以增量形式的PID控制为例，单神经元PID控制的数学表达式为

式中x1(k)=e(k)，x2(k)=e(k)e(k-1)，x3(k)=e(k)-2e(k-1)+e(k-2)。

与传统PID控制不同，单神经网络PID的三个参数是可以随着相应的学习规则实时变化的，所以整个控制器的控制效果也是随着时间而变化的。

2.3 神经网络学习算法

神经网络学习算法是神经网络智能控制的关键部分，神经网络通过学习算法实现自适应、自学习的能力。目前神经网络学习算法可分为有监督学习、无监督学习两大类，本文选用的是有监督的Delta学习规则。

定义误差函数为

(3)

其中，r为参考输入，y为实际输出。

Delta学习规则采取最速下降法来调整权值，基本思路是沿着误差准则函数E的负梯度方向不断修正w值，直到E达到最小，具体表达式为

(4)

2.4 稳定性分析

定义单神经网络的输入为e，则输出u为

(5)

把式(3)和式(5)代入到式(4)中得

(6)

其中neti为wi权值前一个神经元的输出。

(7)

其中Δe(k)=e(k+1)-e(k)。

又

(8)

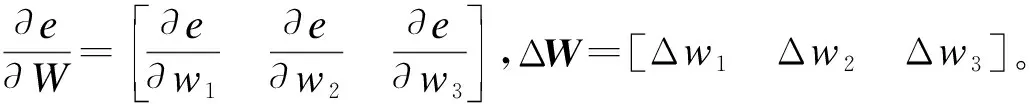
由于e=r-y，则

(9)

结合式(4)，ΔW可写成如下形式

ΔW=

(10)

由式(8)和式(10)得

Δe=-ePTΛP

(11)

将式(11)代入式(7)得

ΔV=[e(k)P]T(-2Λ+ΛPPTΛ)[e(k)P]

(12)

则当-2Λ+ΛPPTΛ<0，有ΔV<0，表明随着t的增加，e(t)→0，所以当权值取式(5)所示的变化时，控制器是稳定的。

3 Matlab仿真

3.1 单位阶跃控制比较

采用阶跃信号对上述双旋翼模型分别进行传统PID控制和单神经网络PID控制，并进行结果对比，步长都为0.01 s，其中传统PID控制器与单神经网络PID控制器的初始参数设置以及单神经网络PID控制器的学习效率设置如表2所示。

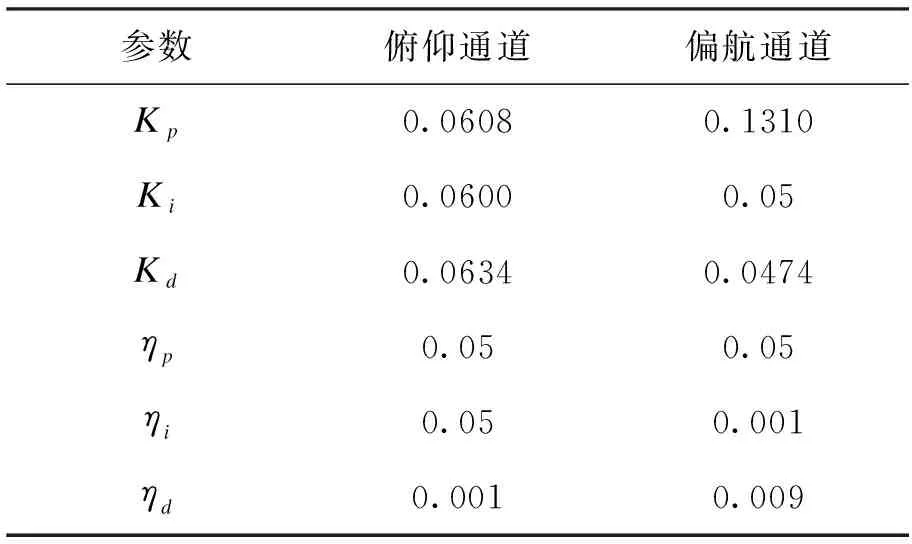
表2 参数设置

仿真结果如图4～图7所示。图4表示在俯仰通道输入阶跃信号时，单神经元网络PID控制与传统PID控制对阶跃信号的跟踪效果，图4(a)中θd为俯仰通道的输入，θsNPID为单神经网络PID控制的跟踪曲线，θPID为传统PID控制的跟踪曲线，图4(b)中esNPID为单神经网络PID控制的跟踪误差曲线，ePID为传统PID控制的跟踪误差曲线。表3表示两种控制方法下的系统性能指标。从跟踪曲线和性能指标来看，单神经元网络控制将系统的调节时间从5.54 s提高到1.43 s，峰值时间从10.87 s提高到2.06 s，表明单神经元网络控制在俯仰通道方面大大提高了系统的快速性。除了性能指标，在15 s后，由于两个通道之间的耦合作用，使得偏航通道输入阶跃信号时对偏航通道产生了影响，从跟踪曲线上看，单神经网络PID控制器强化了各个通道之间的耦合作用。

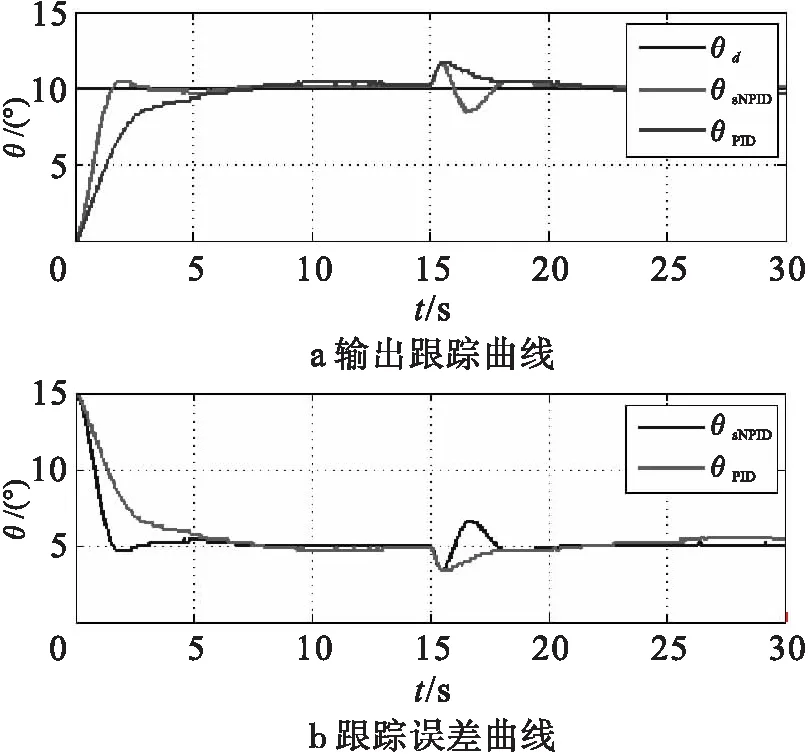
图4 俯仰通道输出跟踪曲线以及跟踪误差曲线(阶跃信号)

图5表示在偏航通道输入阶跃信号时，单神经元网络PID控制与传统PID控制对阶跃信号的跟踪效果，图5(a)中ψd为偏航通道的输入，ψsNPID为单神经网络PID控制的跟踪曲线，ψPID为传统PID控制的跟踪曲线，图5(b)中esNPID为单神经网络PID控制的跟踪误差曲线，ePID为传统PID控制的跟踪误差曲线。表4表示两种控制方法下系统性能指标。从跟踪曲线和性能指标来看，单神经元网络控制将系统的调节时间从19.07 s缩短到1.34 s，跟踪输入的效率明显要远高于传统PID控制，表明单神经元网络控制在偏航通道方面也大大提高了系统的快速性和准确性。

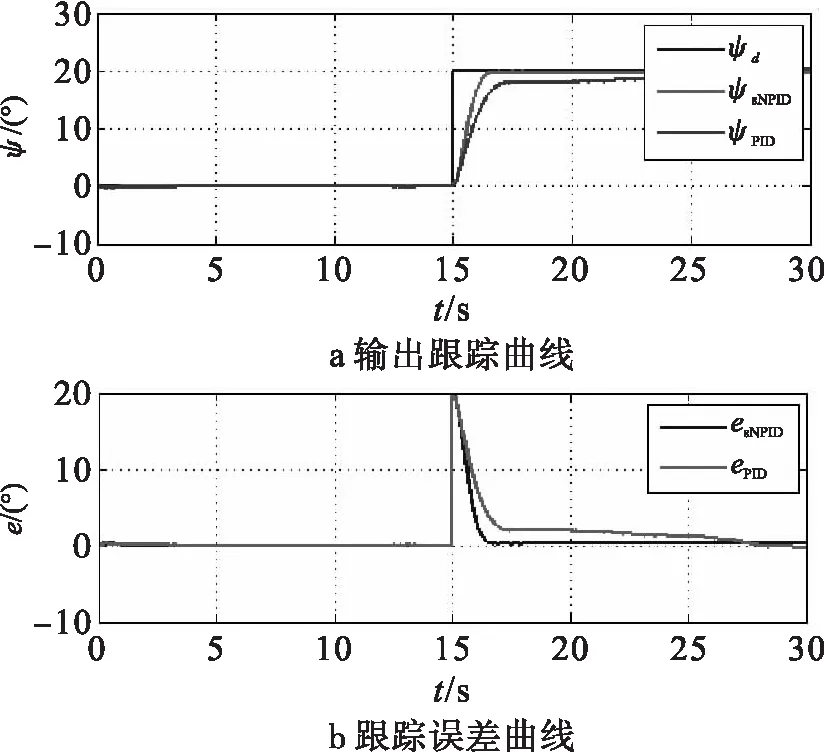
图5 偏航通道输出跟踪曲线以及跟踪误差曲线(阶跃信号)

控制方法超调量/%峰值时间/s调节时间/s单神经元网络PID控制--1.34传统PID控制--19.07

图6表示输入为阶跃信号时俯仰通道和偏航通道的单神经元网络PID控制系统权值变化曲线。可以看出，在俯仰通道中单神经元网络PID控制的比例增益Kp和积分增益Ki有大幅度增加，比例增益的增加可以减小系统的阻尼比，提高系统快速性；积分增益的增加能够消除稳态误差。在偏航通道中单神经元网络PID控制的比例增益Kp、微分增益Kd有大幅度增加，微分增益Kd的增加可以在不改变无阻尼振荡频率的情况下增加系统的阻尼，提高了系统的快速性。

能量消耗是评价控制器性能的一个重要指标，能量消耗越低控制器性能越好[18]。本文系统中能耗为电机的电能消耗，所以能耗指标定义为

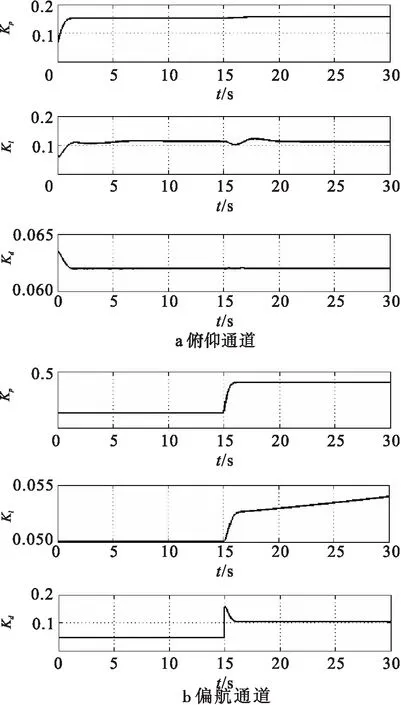
图6 单神经元网络PID控制系统权值变化曲线(阶跃信号)

(13)

从式(13)中可以看出电压是判断电能消耗的一个重要指标。图7表示俯仰通道和偏航通道电机的输入电压。图7(a)中VpsNPID为使用单神经网络PID控制时俯仰电机电压的变化曲线，VpPID为使用传统PID控制时俯仰电机电压的变化曲线，图7(b)中VysNPID为使用单神经网络PID控制时偏航电机电压的变化曲线，VyPID为使用传统PID控制时偏航电机电压的变化曲线。从图中可以看出单神经网络PID控制的电机电压在开始时相对传统PID控制的电机电压来说比较高，但是很快就稳定在低电压处，说明单神经网络PID控制对系统的控制更快。在15S中由于俯仰通道和偏航通道的耦合作用导致电机的电压大幅度上升。由试验数据可得，单神经元网络PID控制的俯仰通道能耗为186.147 V2·s，传统PID控制的俯仰通道能耗为271.936 7 V2·s，采用单神经元网络PID控制后能耗下降了31.55%。单神经元网络PID控制的偏航通道能耗为682.859 1 V2·s，传统PID控制的偏航通道能耗为790.312 6 V2·s，采用单神经元网络PID控制后能耗下降了13.6%。因此，在输入为阶跃信号时单神经元网络PID控制能够大大降低系统的能耗。

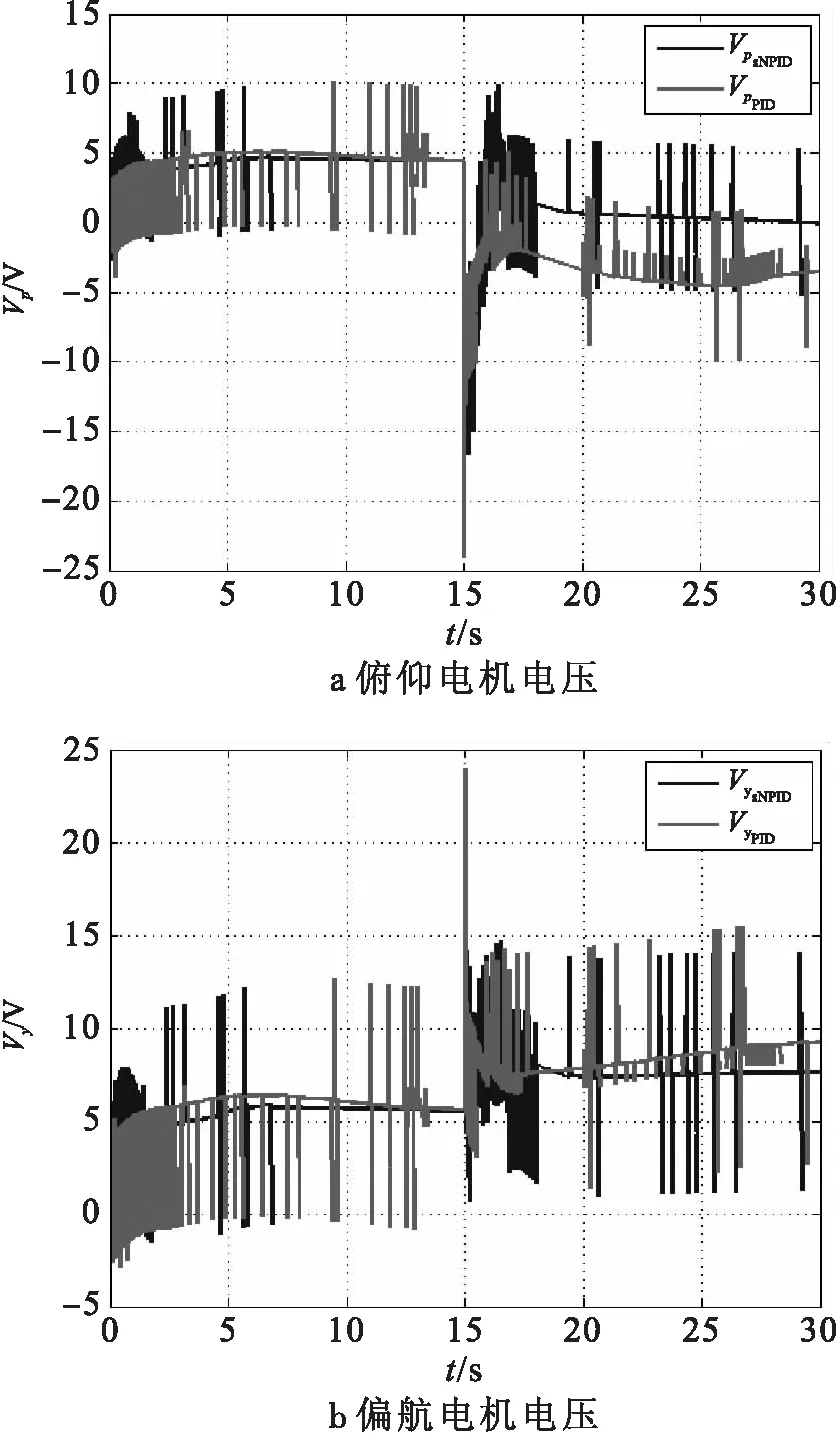
图7 俯仰电机电压和偏航电机电压(阶跃信号)

表5为输入为阶跃信号时的总能耗指标数据。表中总能耗表示为偏航电机能耗与俯仰电机能耗之和，从表中数据可以看出，单神经元网络PID控制能耗与传统PID控制相比下降了18.19%。

表5 总能耗指标数据表(阶跃信号)

3.2 正弦信号控制比较

由于阶跃信号过于简单，且只使用一种输入进行对比试验不能验证控制器对多种信号的适应能力，所以采用正弦信号对传统PID控制系统和单神经元网络PID控制系统再次进行对比测试，正弦信号的频率为0.01 Hz，控制器的初始参数设置和学习参数设置与采用阶跃信号时相同。

图8表示在俯仰通道输入正弦信号时，单神经元网络PID控制与传统PID控制对正弦信号的跟踪效果，图8(a)中θd为俯仰通道的输入，θsNPID为单神经网络PID控制的跟踪曲线，θPID为传统PID控制的跟踪曲线，图8(b)中esNPID为单神经网络PID控制的跟踪误差曲线，ePID为传统PID控制的跟踪误差曲线。表6表示两种控制方法下的系统性能指标。从跟踪曲线和性能指标可以看出，单神经元网络控制将幅值误差由原来的50.8%降低到10.75%，相位差从73.8°减小到了15.12°，大大改善了系统性能，且单神经网络控制的峰值与输入的峰值相差不大，很好地保持了输入的信号特性。

图8 俯仰通道输出跟踪曲线以及跟踪误差曲线(正弦信号)

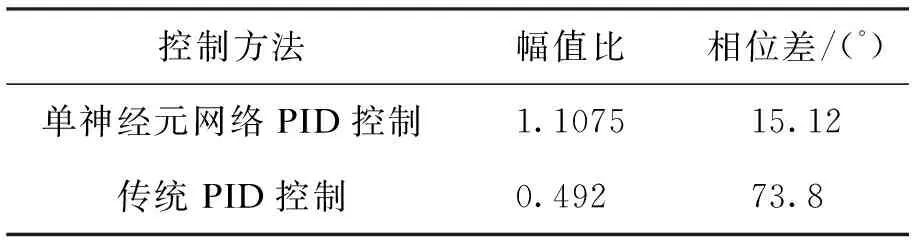
控制方法幅值比相位差/(°)单神经元网络PID控制1.107515.12传统PID控制0.49273.8

图9表示在偏航通道输入正弦信号时，单神经元网络PID控制与传统PID控制对正弦信号的跟踪效果，图9(a)中ψd为偏航通道的输入，ψsNPID为单神经网络PID控制的跟踪曲线，ψPID为传统PID控制的跟踪曲线，图9(b)中esNPID为单神经网络PID控制的跟踪误差曲线，ePID为传统PID控制的跟踪误差曲线。表7表示两种控制方法下的系统性能指标。从跟踪情况和性能指标来看，单神经元网络控制下的幅值比为0.86，相位差为18°，并且跟踪误差仍然在缩小。但是在使用传统PID控制的情况下，稳态输出几乎成一条直线，可见传统PID控制下的偏航通道对频率为0.01 Hz的正弦波几乎没有跟踪能力。

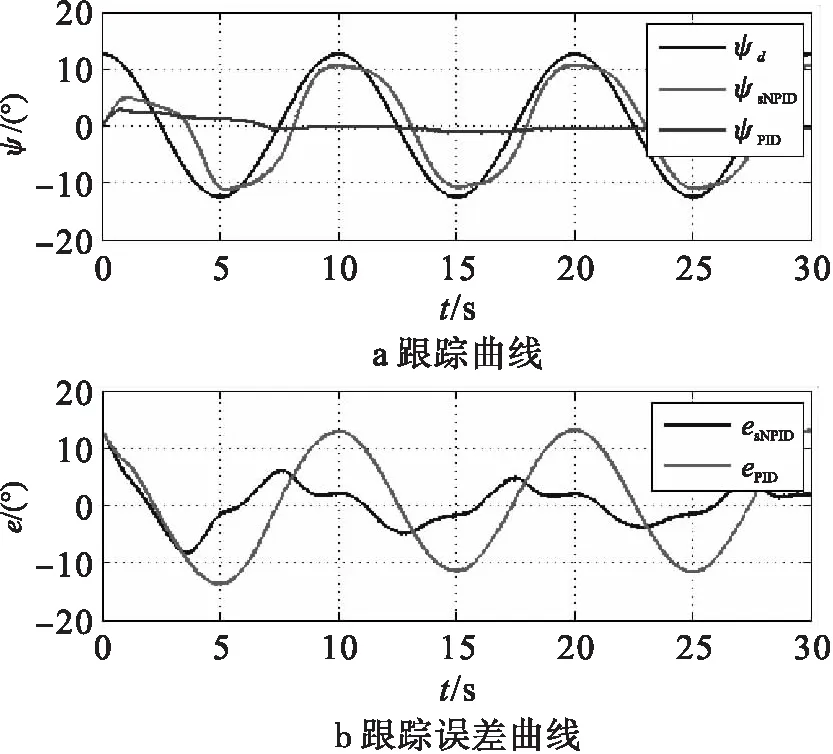
图9 偏航通道输出跟踪曲线以及跟踪误差曲线(正弦信号)

控制方法幅值比相位差/(°)单神经元网络PID控制0.8618传统PID控制--

图10表示输入为正弦信号时俯仰通道和偏航通道的单神经元网络PID控制系统权值变化曲线。由于一开始累积误差比较大，所以使积分增益开始时上升较快，促进系统能够更快地消除误差。从比例增益方面来看，比例增益增加的趋势越来越平缓，说明实际输出与参考输入之间的误差正在逐步缩小。

图11表示输入为正弦信号时俯仰通道和偏航通道电机的输入电压，图11(a)中VpsNPID为使用单神经网络PID控制时俯仰电机电压的变化曲线，VpPID为使用传统PID控制时俯仰电机电压的变化曲线，图11(b)中VysNPID为使用单神经网络PID控制时偏航电机电压的变化曲线，VyPID为使用传统PID控制时偏航电机电压的变化曲线。由试验数据可得，输入为正弦信号时单神经元网络PID控制的俯仰通道能耗为928.6103 V2·s，传统PID控制的俯仰通道能耗为578.615 3 V2·s，采用单神经元网络PID控制后，能耗提高了60.49%。单神经元网络PID控制的偏航通道能耗为671.740 4 V2·s，传统PID控制的偏航通道能耗为443.563 5 V2·s，采用单神经元网络PID控制后，能耗提高了51.44%。

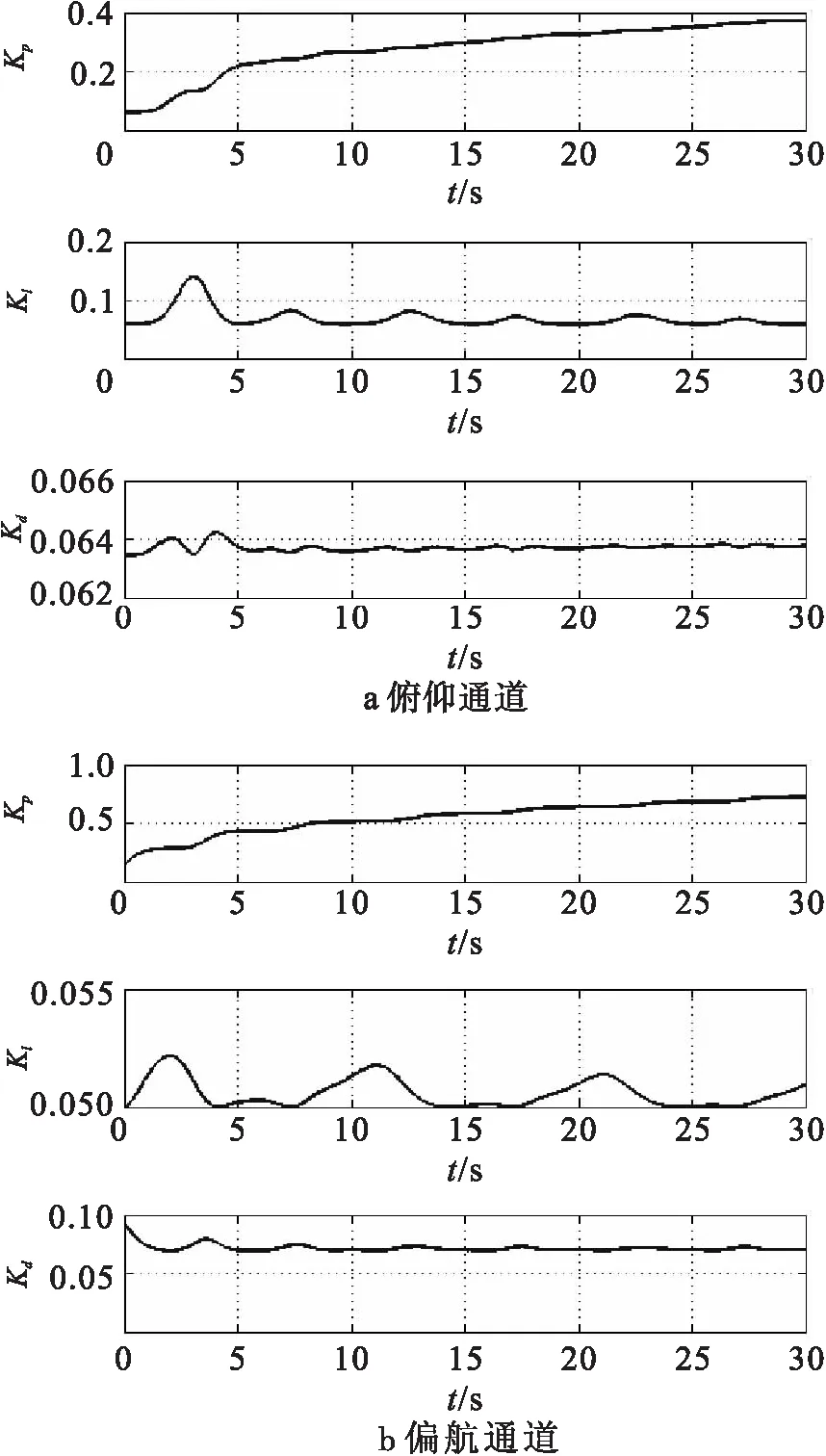
图10 单神经元网络PID控制系统权值变化曲线(正弦信号)

表8为输入为正弦信号时的总能耗指标数据。表中总能耗表示为偏航电机能耗与俯仰电机能耗之和。从表中数据可以看出，单神经元网络PID控制能耗与传统PID控制相比提高了56.56%。在输入为正弦信号时，由于单神经网络控制比传统PID控制更稳定、更快速，具有更好的控制性能，并且在偏航通道传统PID控制对正弦信号失去了跟踪能力，所以单神经网络控制的总能耗要大于传统PID控制的总能耗。

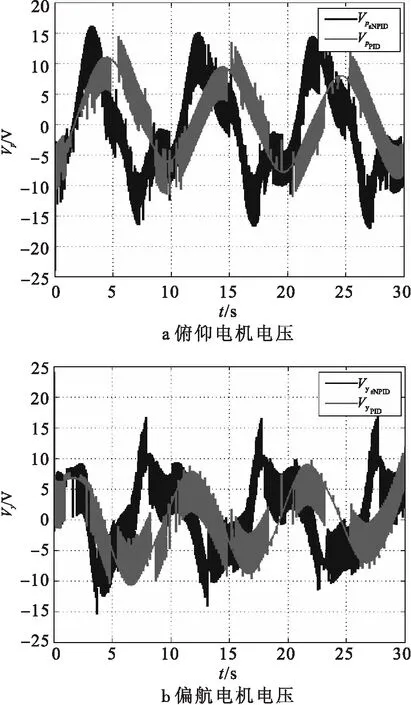
图11 俯仰电机电压和偏航电机电压(正弦信号)

控制方法总能耗/(V2·s)单神经元网络PID控制1600.4传统PID控制1022.2

4 结论

本文通过选用双旋翼实验平台实物作为控制对象，将单神经网络PID控制和传统PID控制在相同的参数条件下进行实物模拟仿真对比。从结果可以看出：单神经网络PID控制调节速度更快，超调更小，大大提高了系统的快速性，对不同类型信号的适应能力更强，而且在实验平台中单神经网络PID控制还强化了各个通道之间的耦合作用，大幅度减少控制器所消耗的能量，更具有效性和实用性。因此，单神经网络PID控制在航空航天领域具有更好的控制性能与应用前景。