基于视频序列的人体三维重建

吴涛，叶炼，柯颖悦

（武汉理工大学，湖北武汉，430000）

引言

基于图像的三维重建的研究目的是利用计算机对物体二维图像信息进行处理，进而得到物体的三维信息，还原出其三维模型。人体三维重建是三维重建技术的一个重要方面，广泛用于医学、人体测量、游戏等领域，具有相当高的研究价值。

人体三维重建的方法主要有基于点云的方法、基于图像的方法、基于点云与图像相结合的方法。

基于点云的方法，是利用激光扫描仪采集人体表面的点云信息，，然后对简化处理采集得来的点云数据，之后对处理后的点云数据进行三角网格化，最后恢复出人体的三维表面模型。基于点云的方法可以有效得到高精度的三维人体模型，但其成本较高，且对计算机资源有较高的要求，所以它主要应用于一些对精度有特殊要求的场景。基于点云的方法的主要步骤包括以下几步：

（1）点云数据采集

首先利用三维扫描仪获得人体的点云信息，由于在扫描过程中易受到外界环境因素的干扰，因此，需要对点云数据进行预处理。剔除点云数据中的不稳定点和错误点。另一方面，普通的扫描仪得到的点云数据比较稠密，如果直接进行使用将花费不必要的计算机资源。因此，还需要对得到的点云数据进行简化处理以简化后续处理的计算与存储。

（2）点云配准

利用公共区域的同名点进行两两匹配，将多组点云数据映射到一个统一的世界坐标系。新的点云数据为后续的统一计算提供了便利，其中最典型的精配准方法为ICP算法。

（3）三维重建

多组点云数据在配准后出现的点云重叠与冗余问题，需要对点云数据去冗余。对简化的点云数据进行三角网格化处理，进而恢复出三维人体模型，它展示了人体的三维表面信息。

基于图像的方法，即使用直接拍摄到的照片进行三维重建。其三维重建方法主要有立体视觉法、运动图像序列法、光度立体学等。基于视频序列的三维重建方法是从SFM技术[1-3]出发，该技术可以同时恢复相机的运动轨迹和三维结构。

基于点云的方法尽管精度较高，但是无法获得物体的纹理信息且成本高昂，而基于图像的的方法速度受到限制孩子，精度也不够高，而基于结合点云与图像的深度相机的方法结合了前面两种方法的优点，利用深度相机可以得到物体的几何结构与纹理映射，进而得到较高真实度的三维模型。

1 主要技术

1.1 相机标定

计算机视觉研究领域有三种常见的坐标系：像素坐标系、图像坐标系、相机坐标系。我们采用针孔模型，使用SFM[1-3]算法同时得到场景的三维结构和相机姿势。

1.2 深度恢复

在这一阶段，我们对已选取的若干段视频序列的每帧图像求解深度图，使用图像分割技术来提升部分没有特征区域深度恢复的质量，最后对前述序列进行集束调整的迭代以优化图像序列。

1.3 特征匹配

特征匹配主要用来进行图像之间的检索，特征匹配的方法主要有由Lowe[4]等人提出的SIFT尺度不变特征变换算法、由Bay[5]等人提出加速鲁棒的SURF算法、由Rosten[6]等人提出的FAST算法，SIFT算法具有对光不敏感、尺度不变性和旋转不变性等优点[1]。故本文采用SIFT算法进行特征匹配。

2 多序列特征匹配与模型重建

2.1 多序列特征匹配

特征匹配的结果会影响到序列对齐的质量，这决定了三维模型重建结果的准确性。通常的双目立体视觉是建立在对应点的视差基础上，因此两幅图像中各点的匹配关系成为立体视觉技研究中的一个极其重要的问题。如果视角发生很大变化，会造成尺度和光照的明显变化，图像之间会发生一定的旋转。这些因素对特征匹配有很大的影响。人们研究了许多约束方法来减少对应点的匹配错误，期望达到更好的匹配效果，通常特征匹配的方法是相关匹配。在这里，我们选择SIFT用作特征描述子用于序列间的特征匹配。

首先，分别取两幅图像序列，我们把P中的每一帧图像和Q中所有的进行特征匹配，即总共有组图像进行特征匹配。然后从这些组中选出一组匹配点的重投影误差最低的图像组，公式化的表达形式如式（1）：

目标函数是使得式（3-1）达到极小值，在实际没有切实简单的方法直接优化上式并求解。因此，为了简化求解过程，我们做了适当的假设，假设在两个序列P和Q间存在且只存在一个相似变换，这样序列P中的点和序列Q中与其相对应的点之间存在这样的对应关系，如式（2）所示：

其次，假设已经知道了k个相对应的点，序列P中的记为和序列Q中的记为，那么要解决的问题变成了下式（3）：

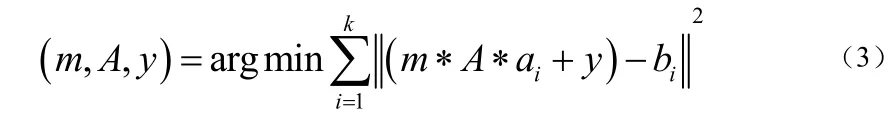
为了简化求解过程，我们先根据匹配的特征点确定尺度变量m，依式（4）所示：

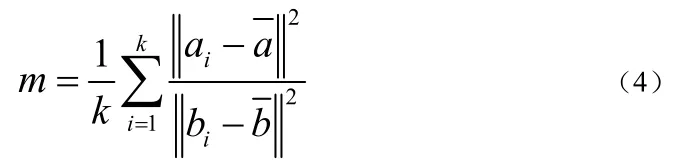
式（4）中的和分别是a和b的重心。在确定了以后，那么上面的式（3）可以变化写成下式的（5）：

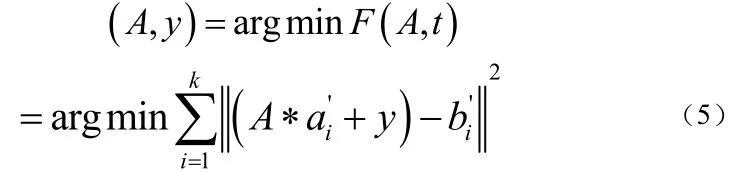
其中的。假设A不变，对F关于y求导得到下式（6）：

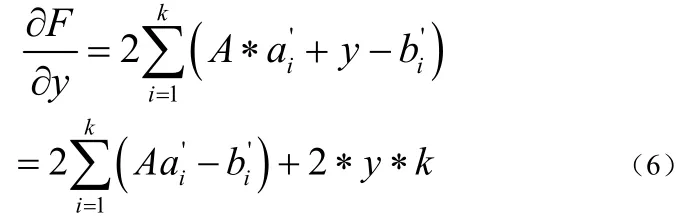
将式（7）中关于y的表达式代入式（5）可以得到如下式（8）：

据此可以推导出式（9）：

然后将（9）中的表达式展开计算可得到如下式（10）：

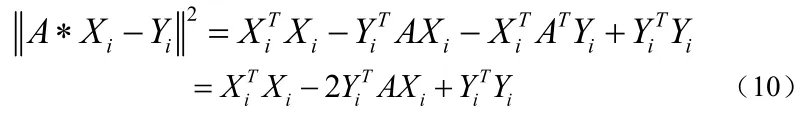
最初的问题转化为（11）：

上式中的X和Y都是3k´的矩阵，在代数中tr代表矩阵的迹。

令,对B做SVD分解，如下式（12）所示：

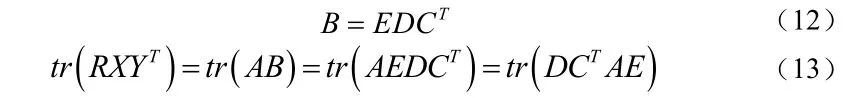
E和C都是正交矩阵，由正交矩阵的性质，可得同样也是正交矩阵，那么可以得到下式（14）和式（15）所示的关系：

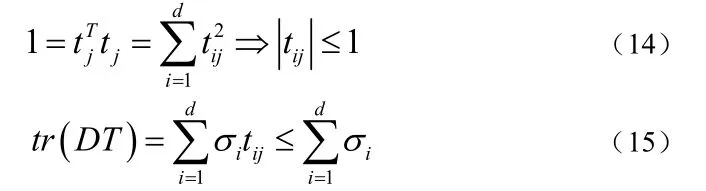
由式（15）可知，如果要使达到极大值，就必须使得，而T是正交矩阵，故T必然是单位矩阵，即可以得到下式（16）

依照上式（16）求出的正交矩阵必定是最优的，可是也有可能这个矩阵是反射矩阵。所以，一旦我们求解得到的矩阵是反射矩阵，那么我们还需要调整相应的结果，寻求下一个相对最符合要求的次优解[7]。

因为不同序列的图像之间的视角变化差异较大，为了降低因视角变换给求解所带来的负面影响，对于每幅图像，我们都会在多视角下生成不同的投影[8-9]。

对于每一幅投影图像，我们都会进行特征检测和匹配，然后再把匹配的结果投影到原始给定的图像上。

在求解SRT时，深度误差的产生会对结果产生影响，为了解决这个问题，我们采用了基于RANSAC的迭代分层式求解方法。

在初始状态，我们使用的所有匹配的特征点计算 SRT。理论上，只有三个相应的点可以计算为SRT。根据从上层获得的SRT，我们计算匹配点的投影误差，如公式（1），然后拒绝匹配点的重投影误差大于一定的阈值，并保留匹配点应用到下一级的输入。

必须要注意的是，在初始层的时候，要选择比较大的重投影误差阈值，这一措施保证了正确的匹配点不被错误的剔除掉。随着层数越大，重投影误差阈值随之动态逐渐减小。通过这些方法，我们可以逐层消除重投影误差较大的点。保留下来的匹配图像对其中的大部分都可以保持颜色的一致性和几何的一致性，有可能仍然存在误差较大的图像对，因此不能用所有的图像对参与SRT的计算，我们从所有的有效匹配图像中选出重投影误差尽可能小同时匹配特征点数尽可能多的一对图像进行SRT的求解。

考虑到需要持续减小深度误差对特征匹配的干扰，在特征匹配之前，我们需要对深度图进行一致性检验。对于每一个位置，利用深度投影到相邻多帧 ，然后通过反投影到当前帧，如果重投影误差大于某一阈值，则标记当前位置的深度值无效。如下式（17），表示处深度值是有效地，否则表示无效。

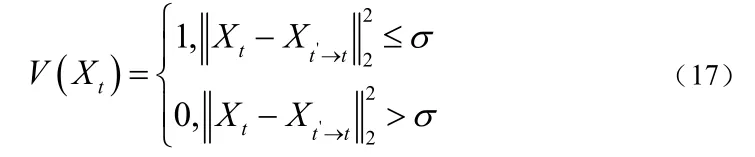
结果发现，如果匹配点聚集在图像的一个小区域，就会产生较大的对齐错误[10]。因为假设利用欧式距离计算出所有的匹配点对很近，那么根据这些点对计算得到的SRT更容易受到深度值的影响，深度上的的极小的误差也会造成对齐结果的很大偏离。考虑到这些，我们对匹配的特征点对进行稀疏采样:对一对新的匹配点，检查邻域范围内是否存在其他的匹配对。如果有，把这个放在赛点上。事实上，这种方法相当于在特征点均匀分布上的施加了限制。

2.2 多视图融合

多视图融合的目的是获得每帧深度图所对应的三维点集，并通过重投影深度误差统计剔除部分不精确的三维点;然后将多帧的三维点集合并成场景整体的三维点云，并剔除其中重复冗余的三维点;得到可靠性较高但规模较小的点云。

本部分采取基于多视图深度采样[11]的方法。首先获得每帧深度图的三维采样点集合，然后给每个三维采样点统计其在相邻帧上的投影深度误差，根据给定的阈值，剔除误差较大的三维点，深度误差计算方法如下式（18）：

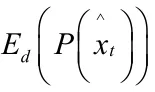
对三位采样点集合进行多帧之间的融合以获得场景完整的三维点云，相对而言，最简单直接的融合多帧三维采样点的方法是取交集。然而多帧视图之间存在许多重叠区域，这会导致直接求交集所获得的三维点云存在很多冗余的三维点，重复的三维点集不仅会大大增加云数据量还会降低模型的精确度。所以接下来需要对每个三维采样点计算深度置信度，剔除掉重复的三维点，通过置信度排序实现多帧三维点采样点的无重复融合。利用三维点在相邻帧的重投影颜色误差来计算其深度置信度，以此衡量该点的精度，置信度计算方法如下式（19）

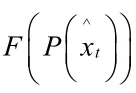
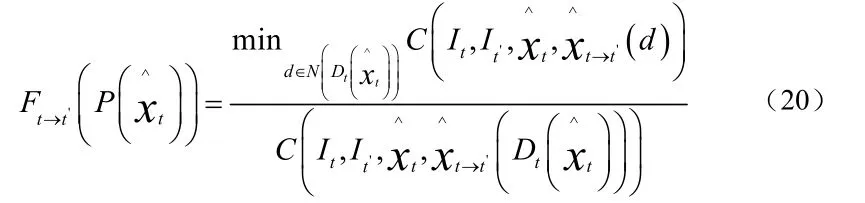
为二维点利用深度重投影的投影点，表示神队友邻域范围内的2K个深度值集合，表示像素衍射差值平方和误差。

把所有采样点的深度置信度都计算之后，依照置信度由高到低的顺序对每帧的三维点集合进行排序并剔除不精确采样点。然后依据归并排序的方法对视频序列中的若干帧三维采样点进行排序。为了排除合并和排序过程中的重复采样点，我们以当前采样点为中心半径R的窗口区域投影到相邻多帧，并去除投影区域中的每一个三维采样点。利用上述方法寻找并移除所有其余帧上的重复采样点，从而保证融合而成的三维点云中不存在重复冗余。由于依照深度置信度由高到低的顺序做归并排序，因此能够保证融合成的三维点云具有最高的精度，同时剔除较低精度的重复三维点。

3 基于模版的深度优化

3.1 Daisy描述子

Daisy是一种用于稠密特征提取的快速计算局部图像特征描述子。它的本质思想是分块统计梯度方向直方图。不同于SIFT，Daisy改进了分块的策略，利用高斯卷积进行分块汇聚，因此利用高斯卷积的可快速计算性可以快速稠密地提取特征描述子。

3.2 鲁棒的模版与模型对齐方法

对齐方法是三维重建领域研究的一个重要问题。常用的对齐方法有迭代最近点算法和基于RANSAC的算法。两种算法均需要提供初始的对应点，当点集的状态差别很大，算法就不适用了。

针对这个问题，提出了一种新的模型对齐方法。人体模型的主方向是沿着身高的方向，次方向是沿着两臂伸展的方向的。利用这一事实，我们的模型对齐方法基于PCA技术[12]。PCA技术用于减少数据的维度，不仅能保留主要成分，还能消除干扰的噪音。对数据降维而言，假设每个人体模型最多只允许由三个最主要的分量描述，那一定是身高、腰围和胸围这类信息。

我们的模型对齐方法包括主成分分析、模板与模型的对齐和模板变形三个步骤。以下仅介绍对齐和变形部分。

3.3 模板与模型对齐

假设已经知道了两个模型的三个主方向。由于分解得到的三个主方向是线性无关的，所以可以由三个主方向向量对确定旋转矩阵。

为了确定两个模型之间的尺度，我们把模型上的所有点投影到第一个主方向上，记录投影点的最远距离和最近距离。

显然，因为不同人体模型的质量重心和几何中心并不重叠，所以如果计算简单的平移，模型对齐的结果会产生一定的偏差从而影响最终的建模结果。

我们可以选择一个体型等各方面都是标准的人体模型作为实验目标模型，把数据库的 平均模型作为待对齐模型，获取一个大致对齐的结果。

事实上，由PCA技术确定的模型的主方向，其朝向并不显而易见，这会影响模版对齐的结果。想要解决这个问题，可以利用地平面数据和相机的朝向信息。

3.4 模板变形

上面提到的待对齐模型是选择一个三维人体模型数据库，然后对其中的所有模型数据进行平均获得的，用R表示，参考模型是经过多段图片序列融合而得到的，用S表示。我们对R应用4.3中的方法，可以获得一个大致对齐的模型。但R和S之间仍存在较大的对齐误差，因为上面的方法只能解决模型之间主方向的对齐的问题，而并不能解决模型之间的胖瘦程度不一致的问题，因此我们还需要对R进行变形[13]以得到一个与S更加接近的结果。

模板变形的过程使用一个计算几何开源库 CGAL[14]。此外在计算控制点形变位置的过程利用相邻采样点加权的方式，可以在一定程度上提高模型的平滑程度。

4 结束语

本文提出了一种人体三维重建方法，即基于视频序列，利用多序列特征匹配和模版约束两种方法的的人体三维重建方法。我们的系统为了实现多序列特征匹配，利用了一种基于RANSAC的迭代分层式求解法，这种方法可以有效消除由于深度误差带来的影响。为了剔除背景点的干扰，我们通过引入深度信息，对匹配的特征点对投影来实 现。为了减少求解SRT的数值上的误差，我们对匹配特征点进行均匀采样。此外，为了防止出现特征过少，我们对原始的序列分别生成多个视角的图像，在各个视角进行特征检测和匹配，这种方法对特征匹配的稳定性有极大的提高。

[1]Snavely N, Seitz S M, Szeliski R.Modeling the world from internet photo collections[J].International Journal of Computer Vision, 2008, 80(2):189-210.

[2]Lourakis M I A, Argyros A A.SBA:A software package for generic sparse bundle adjustment[J].ACM TRANSACtions on Mathematical Software(TOMS), 2009, 36(1): 2.

[3]Wu C.VisualSFM:A visual structure form motion system[J].URL://home.CS.washington.edu/-ccwu/vsfm, 2011, 9.

[4]Lowe D G.Distinctive image features from scale-invariant keypoints[J].International journal of computer vision, 2004, 60(2): 91-110

[5]Bay H,Tuytelaars T, Van Gool L.Surf:Speeded up robust features[M]/Computer vision-ECCV 2006.Springer Berlin Heidelberg, 2006:404-417

[6]Rosten E, Drummod T.Machine learning for high-speed corner detection[M]/Computer Vision-ECCV 2006.Springer Berlin Heidelberg,2006: 430-443

[7]Sorkine O.Least-squares rigid motion using svd[J].Technical notes, 2009,120: 3.

[8]Yu G, Morel J M.Asift:An algorithm for fully affine invariant comparison[J].Image Processing On Line, 2011.

[9]Wu C, Clipp B, Li X, et a1.3d model matching with viewpoint-invariant patches(vip)[C]//Computer Vision and Pattern Recognition，2008.CVPR 2008.IEEE Conference on.IEEE, 2008: 1-8.

[10]Tan W:Liu H,Dong Z，et a1.Robust monocular SLAM in dynamic environments[C]//Mixed and Augmented Reality(ISMAR), 2013 IEEE International Symposium on.IEEE.2013: 209-218.

[11]姜翰青, 赵长飞, 章国锋, 等.基于多视图深度采样的自然场景三维重建[J].计算机辅助设计与图形学学报, 2015, 27(10): 1805-1815.

[12]Bro R, Smilde A K.Principal component analysis[J].Analytical Methods,2014, 6(9): 2812-2831.

[13]Chao I, Pinkall U, Sanan P, et a1.A simple geometric model for elastic deformations[C]//ACM Transactions on Graphics(TOG).ACM, 2010, 29(4):38.

[14]Fabri A, Pion S.CGAL:the Computational Geometry Algorithms Library[J].Sandia National Laboratory, 2009, 30(200009): 538-539.