基于CM-AFSA算法的碾压混凝土坝热学参数反分析
2018-09-18倪智强
邓 晓,倪智强
(1.重庆水利电力职业技术学院,重庆402160;2.河海大学水利水电学院,江苏南京210098)
在碾压混凝土坝施工和运行过程中,温度场的分布情况对了解大坝质量状况和运行情况至关重要。一般热学参数都是来源于室内试验,由于试验本身存在的误差和随机性较大,通过室内试验得到的热学参数与真实参数相去较远。因此,若能在实际工程中根据实测温度值,通过寻优算法和有限元计算高效准确地反演出大坝的热学参数,则有助于更加准确地了解大坝的状态和运行情况。国内学者朱伯芳[1- 3]、朱岳明[4]等,国外学者Carslaw[5]等结合各种反演方法对混凝土热学参数反演问题进行了求解分析。本文在以往研究的基础上,基于人工鱼群算法并结合云模型理论提出利用CM-AFSA算法对大坝热学参数进行反演分析,并利用反演得到的热学参数对温度场进行正演算,通过对比分析计算值和监测值的拟合程度对该优化算法在参数反演中的应用效果进行评价。
1 CM-AFSA算法
人工鱼群算法(AFSA)由李晓磊[6]于2002年提出,是一种通过模拟自然界鱼群觅食行为来解决生活中寻优问题的算法。其数学模型为:向量X=(x1,x2,…,xn)表示人工鱼的状态,其中,xi(i=1,2,…,n)为待寻优的参数。Y=F(X)表示人工鱼当前状态下的食物浓度;人工鱼i和j之间的距离为dij=‖Xi-Xj‖。另外,Visual为人工鱼的视野范围;Step为人工鱼的可移动步长;Np为人工鱼的总数;TryNumber表示人工鱼觅食最大尝试次数;δ为拥挤度因子。AFSA算法中,每次迭代最优人工鱼状态X及相应食物浓度Y都会被记录在公告牌上并进行实时更新。
虽然AFSA算法[7]具有强鲁棒性,也容易全局收敛,但其后期收敛速度慢、寻优精度低是其存在的问题。基于此,本文拟结合云模型理论改进AFSA算法,提出一种新的高效寻优算法——云人工鱼群算法(CM-AFSA算法),并将其运用于碾压混凝土坝热学参数反演中。
CM-AFSA算法的流程如图1所示,具体步骤为:
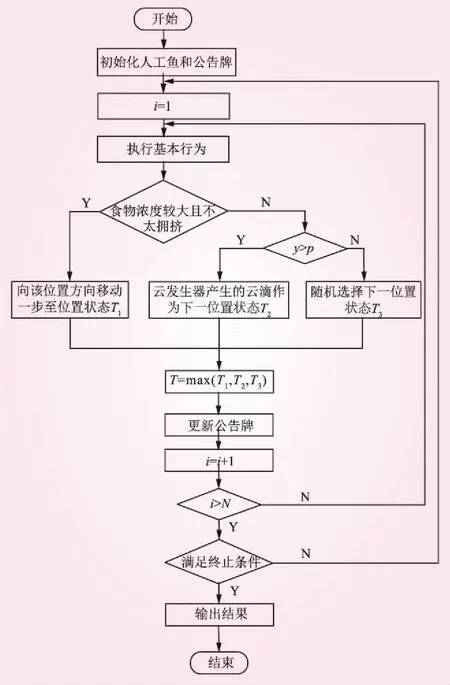
图1 CM-AFSA算法流程
(1)初始化人工鱼。在论域U内随机生成N条人工鱼,形成初始鱼群X=(x1,x2,…,xn),初始化可视域visual,步长Step,迭代次数TryNumber和拥挤度因子δ。
(2)初始化公告牌。对初始鱼群中各个人工鱼个体处的食物浓度进行计算并比较,将浓度最大的对应人工鱼状态及其位置记录于公告牌。
(3)执行基本行为。对N条人工鱼依次分别执行聚群和追尾行为,比较两者中状态更优的将其更新于公告牌,默认行为为觅食行为。对觅食行为本文改用云发生器来模拟,区别于传统AFSA算法,基本步骤为:①令Ex=xi,En=visual/c1,He=En/c2;②若确定度y大于一个随机数p,则由基本云发生器生成的云滴作为人工鱼个体移动到下个位置的依据,否则执行随游行为。
(4)更新公告牌。每条人工鱼执行完行为后都要计算其相应的食物浓度,然后和公告牌上的食物浓度相比,如果比公告牌上的值更优,则更新公告牌的值为人工鱼自身值。
(5)算法终止。当公告牌上的值达到规定的误差界限,则算法停止,输出最优解;否则转到步骤(3)继续。
2 碾压混凝土坝热学参数反分析
2.1 温度场基本理论
三维非稳定温度场[8]需满足的热传导方程为
(1)
初始条件T=T(x,y,z,0)=T0
(2)
第一类边界条件T(t)=f(t)
(3)
(4)
(5)
式中,T0为初始瞬时导热物体内部的温度;Tα为空气温度;α为碾压混凝土的导温系数;θ为绝热系数;n为混凝土表面外法线方向;λ为导热系数;β为表面放热系数。
2.2 参数选择
碾压混凝土坝施工与运行期间,与坝体温度场相关联的参数有导热系数λ、导温系数α、表面散热系数β、混凝土的比热c、绝热温升θ、密度ρ等。通过试验可以直接测出混凝土的密度ρ及比热c,而导热系数λ也可通过α=λ/(cρ)算出,因此,本文选择导温系数α、表面散热系数β、绝热温升θ作为最终反演的参数。
2.3 目标函数建立
目标函数F(Q)可以表示为
(6)
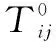
2.4 基于CM-AFSA算法反演热学参数
碾压混凝土坝热学参数反演可以概括为:在给定的条件下,在向量Q的取值空间中寻求一组向量Q0使得目标函数F(Q)取得极小值,向量Q0中的参数α0、β0、θ0则为最终反演参数值。利用CM-AFSA算法反演热学参数的步骤见图2。

图2 利用CM-AFSA算法反演热学参数流程
3 工程实例
某碾压混凝土坝位于我国华东地区,坝顶高程221 m,最大坝高125 m。选取主坝体3号坝段的监测资料进行分析,125.50~143.50 m高程之间每隔9 m布置6支温度计,152.50~170.50 m高程之间每隔9 m布置5支温度计,179.50~188.50 m高程之间每隔9 m布置4支温度计。有限元模型及监测布置图分别见图3和图4。

图3 坝体温度场计算模型

图4 坝体内部温度计布设
由于坝体内部温度监测值比较稳定,因此本文选取内部观测点Z3- 1、Z3- 2、Z3- 3、Z3- 4、Z3- 5、Z3- 6、Z3- 7、Z3- 8的监测资料来反演碾压混凝土坝热学参数。根据工程经验,将碾压混凝土坝热学参数α取0.003~0.004 m/h2,β取30~60 kJ/(m2·h·℃),θ取15~20℃。
初始化算法,定义各参数初值:Np=200,TryNumber=50,visual=2.0,δ=0.625,step=2.5,c1=200,c2=10,p=0.9;最大迭代数为500。将所有参数带入图2,经过反演分析得到最终的结果见表1。

表1 反演所得参数
将表1反演出的参数结果作为已知值,利用三维有限元软件ANSYS正向计算相应的温度值,并将温度计算值与实际工程资料中监测值进行对比,拟合过程见图5(由于测点数比较多,本文只选择测点Z3- 3和Z3- 8来进行分析)。
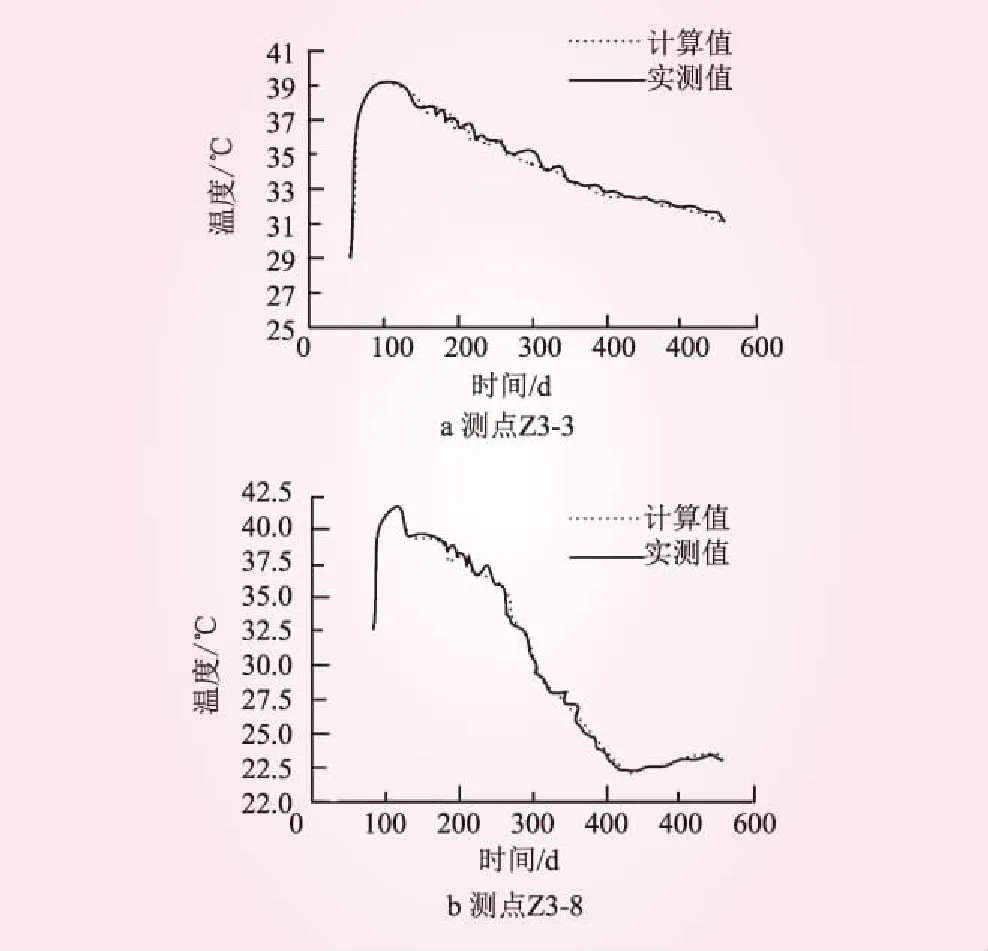
图5 计算值与监测值对比曲线
从图5可以明显看出,利用表1所得参数结果正演算得出的温度计算值与实际工程资料中的温度监测值拟合程度很高,说明利用CM-AFSA算法反演出的碾压混凝土坝热学参数是接近真实值的,基于人工鱼群算法改进的CM-AFSA算法在碾压混凝土坝热学参数反演分析计算中的应用是成功的。
设置结束条件为F(Q)≤0.01,比较CM-AFSA算法与AFSA算法的反演效率,计算结果见表2。

表2 CM-AFSA算法与改进AFSA反演效率对比
从表2可以看出,CM-AFSA算法在相同控制精度下对坝体进行热学参数反分析时搜索时间更短,循环次数更少。因此相比于传统AFSA算法,CM-AFSA算法具有更高的演算效率。
4 结 论
利用云模型理论对传统AFSA算法进行优化,增加了算法的随机性和稳定倾向性,使算法在寻优过程中更加科学而又具有针对性的缩小了搜寻范围,显著提升了算法的精度和效率。结合某碾压混凝土坝实测资料,将该算法通过MATLAB软件编程,反演其热学参数,并利用反演出的热学参数进行温度场的正演算,将得到的温度计算值与实测资料中的真实值进行对比,结果表明,两者的拟合程度很高,验证了CM-AFSA算法的可行性。
