自适应细菌觅食算法求解折扣{0-1}背包问题

刘雪静，贺毅朝，吴聪聪，李 靓

1.河北地质大学 信息工程学院，石家庄 050031

2.中国邮政集团公司 河北省邮政信息技术局，石家庄 050011

1 引言

0-1背包问题（0-1 Knapsack Problem，0-1KP）[1]是典型的组合优化问题，属于NP-complete问题，资源分配、材料切割、货物装载等领域里的许多问题均可建模成0-1KP进行研究。0-1KP有许多不同的形式，折扣{0-1}背包问题（Discount{0-1}Knapsack Problem，D{0-1}KP）是新型的0-1KP。2007年Guldan[2]首先提出了D{0-1}KP，给出了其第一数学模型，贺毅朝等[3]给出了其第二数学模型，两个数学模型描述如下。

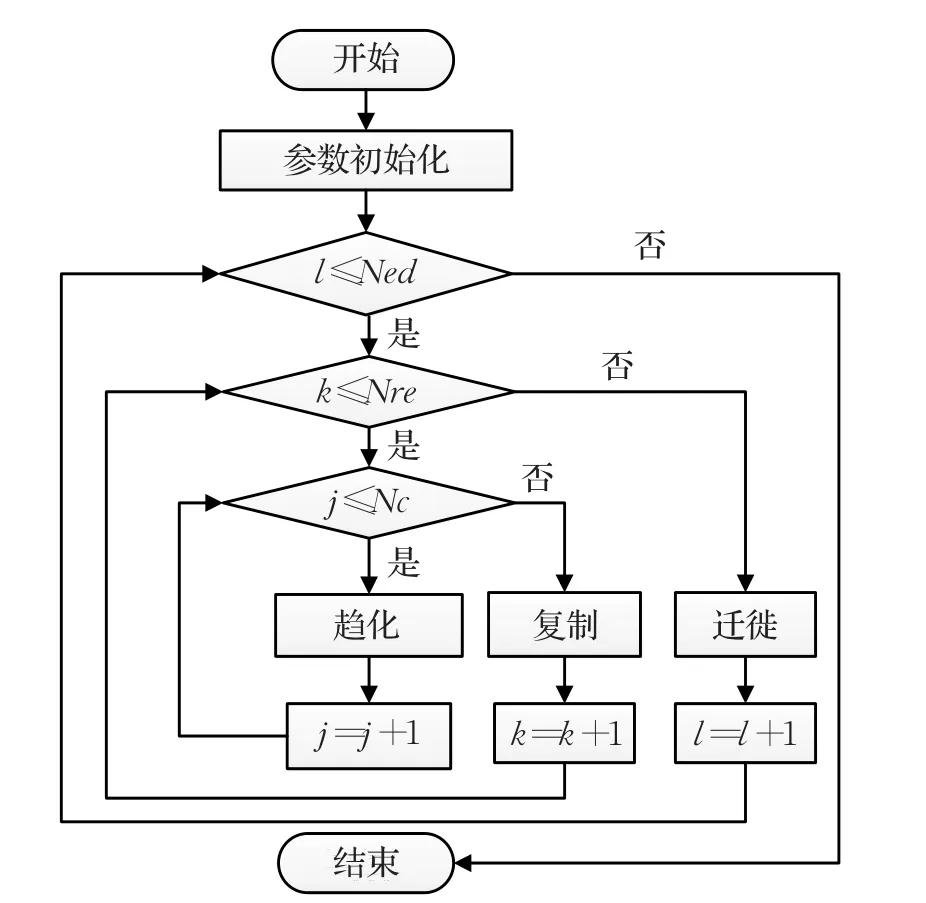
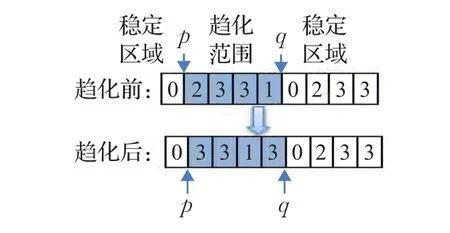
定义1[2]给定n个项集，每一项集(0≤i≤n-1)中均含项3i、3i+1和3i+2，项3i的价值系数为 p3i，重量系数为w3i，项3i+1的价值系数为 p3i+1，重量系数为w3i+1，项3i+2的价值系数为 p3i+2=p3i+p3i+1，折扣重量系数为 w3i+2，且满足 w3i+2＞w3i、w3i+2＞w3i+1和w3i+2

其中，xk(0≤k≤3n-1)的取值表示项k是否被装入背包，xk=1表示项k装入背包，xk=0表示项k未装入。显然，任意的二进制向量X=[x0,x1,…,x3n-1]仅是D{0-1}KP的一个潜在解，只有同时满足约束条件（2）～（4）的X才是D{0-1}KP的一个可行解。

D{0-1}KP的第二数学模型[3]描述如下：

其中，X=[x0,x1,…,xn-1]∈{0,1,2,3}n是n维整型向量为不小于x的最小整数，xi=0表示项集i中没有项装入背包，xi=1表示项3i被装入背包，xi=2表示项3i+1被装入背包，xi=3表示项3i+2被装入背包。整型向量X仅表示D{0-1}KP的一个潜在解，只有满足约束条件（6）和（7）的X 才是D{0-1}KP的一个可行解。

2 相关研究工作

细菌觅食（Bacterial Foraging Optimization，BFO）算法[4]是Passino在研究大肠杆菌吞噬食物行为的基础上提出来的一种仿生随机搜索算法。目前，BFO已被广泛应用于许多领域。崔静静等[5]将BFO进行改进，将其用于求解车间作业调度；王雪松等[6]将细菌的趋化性运动引入到分布估计算法中，提出一种基于细菌觅食行为的分布估计算法；Panda等[7]提出一种基于细菌觅食的面部识别算法；李珺等[8]将多种策略应用到BFO算法中求解高维优化问题；Manikandan等[9]通过将BFO算法与遗传算法相结合求解多目标问题。总之，当前对BFO算法的研究主要体现在对原算法的改进和实际的应用，而改进主要是在趋化操作中引入自适应机制或与其他智能算法相结合。

Guldan[2]首先利用动态规划法进行求解D{0-1}KP的第一数学模型；Rong等[10]将动态规划法与D{0-1}KP的core相结合求解D{0-1}KP。确定性算法求解D{0-1}KP是伪多项式时间的，当各项的重量系数和价值系数较大时，算法不可行。目前，进化算法求解D{0-1}KP取得了许多可以借鉴的研究成果。贺毅朝等[3]提出了D{0-1}KP的第二数学模型和第三数学模型，并率先利用遗传算法进行求解，虽然不能得到最优解，但求得了较好的近似解；吴聪聪等[11]利用改进的蝙蝠算法求解D{0-1}KP，得到较优近似解；刘雪静等[12]利用细菌觅食算法求解D{0-1}KP，得到近似比接近1的近似解，但是耗费时间较多；He等[13]提出了求解D{0-1}KP的二进制粒子群算法；Feng等[14]利用改进的帝王蝶算法求解D{0-1}KP，得到较好的求解结果；刘雪静等[15]利用乌鸦算法求解D{0-1}KP，取得较优解；Zhu等[16]利用差分演化算法求解该问题，并给出了三个高效离散演化算法，求得较好解。由此可见，如何利用进化算法高效、快速求解D{0-1}KP非常值得研究。

3 自适应细菌觅食算法求解D{0-1}KP

3.1 细菌觅食算法

BFO算法是一种新型仿生优化算法，其求解优化问题的一般过程为：产生初始解种群，计算适应度函数值，群体间通过趋化、复制、迁徙进行迭代优化，直至产生最终解。算法如图1所示，其中，S为种群大小，Ned为迁徙次数，Nre为复制次数，Nc为趋化次数，Ns为游动次数，Ped为迁徙概率。图1的一个趋化步骤内，每个细菌按照如下步骤进行：

（1）翻转。产生随机方向向量Δ(i)，进行方向调整，按式（8）、（9）更新细菌的位置，重新计算适应度值。

Pi(j,k,l)代表第i个细菌个体的当前位置，其中，j表示第 j次趋向行为，k代表第k次复制行为，l代表第l次迁徙行为，C(i)为细菌i的趋化步长，V(i,j)为细菌i翻转时的单位随机方向向量。

（2）游动。如果细菌翻转后适应值得到改善，则沿当前方向继续游动，直至适应度值不再改善或在该方向达到预定的最大游动步数。

复制操作是对所有细菌个体按照适应度值降序排序，将排在后面的一半个体删除，剩下的个体进行再生。迁徙操作是对每个细菌以Ped概率随机生成一个新个体并替换原个体，增强细菌的全局搜索能力。

算法1 BFO（其流程图见图1）。

图1 BFO流程图

3.2 自适应趋化策略

BFO算法中，趋化操作对算法来说至关重要。选择较大的步长值，有助于个体快速向着最优位置移动，收敛速度快，但易跳过最优值；选择较小的步长值，细菌个体向最优位置移动的速度过慢，算法效率较低。基于此，本文将BFO的趋化操作加以改进，使改进BFO随着迭代次数的增加，细菌个体选取其中的某一部分维度进行趋化操作，且其趋化范围随着迭代次数的增加而减小，以提高算法的收敛速度和适应度精度。

（1）自适应趋化策略1

针对D{0-1}KP的第一数学模型，假定当前细菌个体编码为（0，0，1，0，1，0，1，0，0，0，0，1，0，1，0），如图2所示，在当前个体上随机选取两个点 p和q，p、q之间的区域作为趋化范围，两侧的两个区域为稳定区域。选择 p、q时使| |

p-q的值随着迭代次数的增加而减小，利于迭代初期在全局范围内搜索最优解，迭代后期在局部范围内搜索最优解。新的游动为p、q范围内的编码在后续操作中逆序存放，稳定区域的编码在后续操作中不变。经过上述变换之后，个体相当于向前游动了一步，对新个体的适应度进行评估，如果新个体适应度值更优，则新个体取代旧个体，并继续下一次操作。

图2 第一种趋化操作

（2）自适应趋化策略2

针对D{0-1}KP的第二数学模型，假定当前编码为（0，2，3，3，1，0，2，3，3），如图3所示，随机选取两个点 p和 q，且的值随着迭代次数的增加而减小。新的游动操作为趋化范围内的编码在后续操作中随机取值，稳定区域的编码在后续操作中不发生改变，其他同上。

图3 第二种趋化操作

将自适应趋化策略引入BFO算法中，得到自适应BFO（Adapative BFO，ABFO）算法。

3.3 求解D{0-1}KP的FirABFO

算法2 FirABFO

1.初始化参数S,Nc,Ns,Nre,Ned,Ped

2. H[i]←Quicksort(pi/wi)(0≤i≤3n-1)

3.生成初始种群P(Xi)(1≤i≤S)并转化为二进制种群B(Xi)，计算适应度 f(B(Xi))

4.forl=1toNed

5. fork=1toNre

6. forj=1toNc

7. fori=1toS

8. 对Xi执行自适应趋化操作1并用GROA优化

9. endfor

10. endfor

11. 复制

12.endfor

13.个体迁徙并利用GROA优化

14.endfor

15.返回最优个体及其适应度

在第2步中，Quicksort为快排序，时间复杂度O(nlbn)，第3步生成初始种群并优化，时间复杂度为O(S×n)，第5步至第14步的时间复杂度为O(S×Nc×Nre×Ned×Ns×n)，故FirABFO的时间复杂度为多项式时间。

3.4 求解D{0-1}KP的SecABFO

针对D{0-1}KP的第二数学模型，随机产生值在[0，4）之间的实型细菌个体，整数编码中的 xi由对应的映射得来。参照文献[3]中新的贪心修复和优化算法（NROA）对X进行处理，将所有的潜在解修正为可行解。故利用ABFO和NROA对D{0-1}KP的第二数学模型求解，得到SecABFO算法。

算法3 SecABFO

1.初始化参数S,Nc,Ns,Nre,Ned,Ped

2. H[i]←Quicksort(pi/wi)(0≤i≤3n-1)

3. 生成初始种群P(Xi)(1≤i≤S)转为整数种群B(Xi)并优化

4.forl=1toNed

5. fork=1toNre

6. forj=1toNc

7. fori=1toS

8. 对Xi执行自适应趋化操作2后利用NROA处理

9. endfor

10. endfor

11. 复制

12. endfor

13. 个体迁徙后利用NROA修复与优化

14.endfor

15.返回最优个体及其适应度

第3步生成初始种群并用贪心策略进行优化，时间复杂度为O(S×n)，第5步至第14步的时间复杂度为O(S×Nc×Nre×Ned×Ns×n)，故SecABFO的时间复杂度为多项式时间。

4 仿真实验与分析

本文仿真实验的四类D{0-1}KP实例分别为：不相关D{0-1}KP实例（Uncorrelated instances of D{0-1}KP，UDKP）、弱相关D{0-1}KP实例（Weakly correlated instances of D{0-1}KP，WDKP）、强相关D{0-1}KP实例（Strongly correlated instances of D{0-1}KP，SDKP）和逆向强相关D{0-1}KP实例（Inversestrongly correlated instances of D{0-1}KP，IDKP），每一类实例中含规模大小为300、600、900、1 200、1 500、1 800、2 100、2 400、2 700、3 000的10个实例，实例生成参照http：//pan.baidu.com/s/1o6MJVEq。

利用FirABFO和SecABFO求解四类D{0-1}KP实例时，参数设置如下：S为30，迭代次数Miter为40，Nc为20，Ns为4，Nre为4，Ned 为2，Ped 为0.25。每个算法分别独立运行100次，结果见表1～表4。其中，Opt为动态规划法（DPDKP）[2]计算出的实例最优值；Best、Worst和Mean分别为100次计算得到最好值、最差值及数学期望，FirEGA算法的数据来自文献[3]，文献[12]中选取每类实例的最优算法FirBFO或SecBFO，MMBO算法的数据来自文献[14]，FDDE算法的数据来自文献[16]。

表1为各算法求解UDKP类实例的结果，图4为6种算法的近似比比较图。由图4（a）可以看出，SecABFO的最优近似比值最小，接近1，是6种算法中最好的；FirABFO在求解UDKP1-UDKP5时与FDDE算法不相上下，在求解UDKP6-UDKP10时近似比值逐渐增大，与其他算法相比，优势逐渐减弱。图4（b）、图4（c）与图4（a）区别不大。总的来说，SecABFO对UDKP类实例的求解性能在6种算法中是最好的，FirABFO的求解性能在大部分实例上优于FirEGA、SecBFO、MMBO，与FDDE算法相比，两种算法各有优劣。

表1 求解UDKP实例的结果

表2 求解WDKP实例的结果

图5为6种算法求解WDKP类实例时的近似比比较图。由图5（a）可以看出，SecABFO的最优近似比值最小，且接近1，是6种算法中最好的；FirABFO在求解WDKP1-WDKP8时仅次于SecABFO，在求解WDKP9-WDKP10时比SecABFO和MMBO略差，且FirABFO的最优近似比值小于1.002。由图5（b）可以看出FirABFO和SecABFO的曲线变化不大，近似比值仍然最小，算法性能最好，但其他算法的曲线都有变化，值略有增大。由图5（c）可以看出，各算法曲线浮动较大，但FirABFO和SecABFO的值仍然最小。故求解WDKP类实例时，FirABFO和SecABFO的求解性能最好，优于其他4种算法。

图6是6种算法求解SDKP类实例的近似比比较图。由图6（a）可以看出，SecABFO的最优近似比值最小，是6种算法中最好的；FirABFO在求解SDKP1-SDKP7时仅次于SecABFO，在求解SDKP8-SDKP10时优于FirEGA和FirBFO，劣于SecABFO和FDDE，与MMBO不相上下。由图6（b）和图6（c）可以看出6种算法的平均近似比值和最差近似比值比图6（a）都略有增大，曲线稍有浮动，但FirABFO和SecABFO算法性能最好。故FirABFO和SecABFO是求解SDKP类实例的最优算法。

图4 6种算法求解UDKP实例的近似比比较图

图5 6种算法求解WDKP实例的近似比比较图

图6 6种算法求解SDKP实例的近似比比较图

图7 5种算法求解IDKP实例的近似比比较图

图8 FirABFO和SecABFO在四类实例上的最优近似比

由于文献[14]中未提供MMBO求解IDKP类实例的结果，故图7为5种算法的近似比值比较图。由图7可以看出，除FirEGA和FDDE外，其余3种算法近似比值相对比较集中，FirBFO、FirABFO和SecABFO近似比值非常接近1，这3条曲线基本重合。故FirBFO、FirABFO和SecABFO的求解性能在5种算法中最好。

图9 FirABFO和SecABFO的平均收敛曲线比较

图8 更直观地显示出FirABFO和SecABFO在4组实例上的求解性能。由图8（a）～（c）可以看出，SecABFO的近似比值小于FirABFO，故在求解UDKP、WDKP和SDKP类实例时SecABFO求解性能优于FirABFO；图8（d）的纵坐标取值最小，两种算法的最优近似比的最大值远远小于1.000 1，基本等于1，即两种算法在IDKP类实例上的求解性能都很好，且仅在IDKP7、IDKP8和IDKP10上FirABFO优于SecABFO。总的来说，FirABFO和SecABFO在4组实例上的求解性能IDKP最优，WDKP次之，SDKP第三，UDKP最差，但是最差的近似比值也在1.066以下。由图8还可以看出 SecABFO在对4类D{0-1}KP实例求解时，近似比值更小，更接近1，因此更适合求解D{0-1}KP。

结论：对于规模大且项的价值系数和重量系数均在大范围内随机取值的4类D{0-1}KP实例，FirABFO和SecABFO均能够快速求得一个近似比接近于1的近似解，因此它们都是适于求解大规模难D{0-1}KP的有效且实用的进化算法。从算法求得的最好结果和算法的平均求解性能来看，SecABFO的求解效果明显优于FirABFO。

5 结束语

本文研究如何利用改进的自适应趋化策略的细菌觅食算法求解D{0-1}KP问题。针对细菌个体的两种编码方法，给出了求解D{0-1}KP的FirABFO和SecABFO算法。通过对4类大规模D{0-1}KP实例的计算结果分析表明：FirABFO和SecABFO的求解性能非常好，均不受实例中各项的价值系数、重量系数和背包载重的大小影响，能够快速求得一个近似比接近于1的近似解，因此均为求解D{0-1}KP实例的实用进化算法。